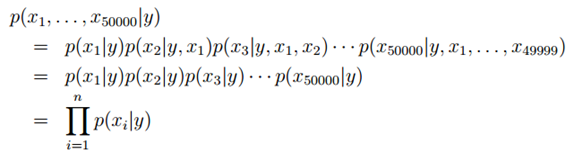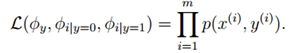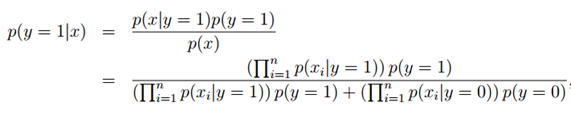StanFord ML 笔记第四部分

第四部分：

　　　　1.生成学习法 generate learning algorithm

　　　　2.高斯判别分析 Gaussian Discriminant Analysis

　　　　3.朴素贝叶斯 Navie Bayes

　　　　4.拉普拉斯平滑 Navie Bayes

一、生成学习法generate learning algorithm：

　　　　二类分类问题，不管是感知器算法还是逻辑斯蒂回归算法，都是在解空间中寻找一条直线从而把两种类别的样例分开，对于新的样例只要判断在直线的哪一侧即可；这种直接对问题求解的方法可以成为判别学习方法（discriminative learning algorithm）。而生成学习算法则是对两个类别分别进行建模，用新的样例去匹配两个模型，匹配度较高的作为新样例的类别，比如良性肿瘤与恶性肿瘤的分类，首先对两个类别分别建模，比如分别计算两类肿瘤是否扩散的概率，计算肿瘤大小大于某个值的概率等等；再比如狗与大象的分类，分别对狗与大象建模，比如计算体重大于某个值的概率，鼻子长度大于某个值的概率等等。

比如说良性肿瘤和恶性肿瘤的问题，对良性肿瘤建立model1（y=0），对恶性肿瘤建立model2（y=1），p(x|y=0)表示是良性肿瘤的概率,p(x|y=1)表示是恶性肿瘤的概率.

根据贝叶斯公式（Bayes rule）推导出y在给定x的概率为：

　　　　注释如下：

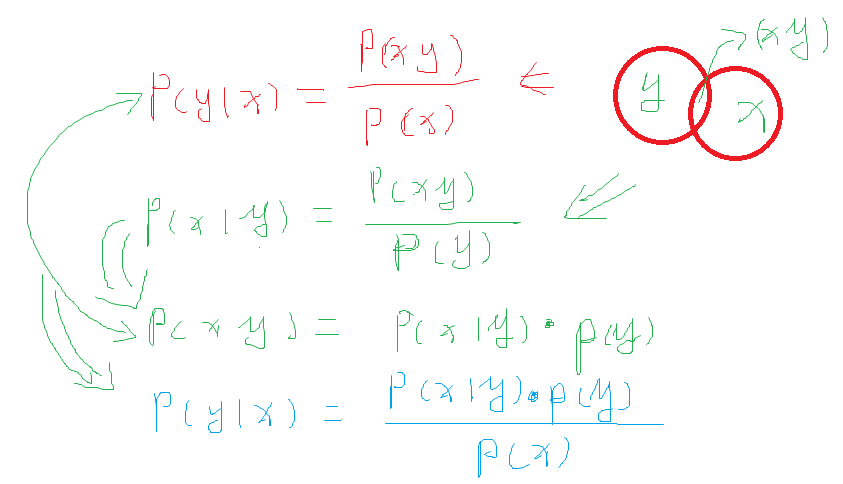
二、高斯判别分析 Gaussian Discriminant Analysis：

　　　　先看概念：高维高斯分布的理解

　　1. 如何描述问题？

　　1.0 问题的假设是什么？

　　　　这个模型对于数据有非常强的假设：

　　　　它假设变量是连续的，并且每一个特征都符合正态分布（即高斯分布）

　　　　即输入特征满足多元正态分布（后面来讲）

　　　　对应一个二元分类问题 y = h(x), 需要满足下面的分布：

NewImage

　　1.1 如何用模型描述问题？

　　　　由于有了上面的假设，问题可以描述为：

NewImage

　　　　当需要分类是，通过贝叶斯公式计算其属于某一类的概率：

NewImage

　　1.2 如何定义求解目标？

　　　　算法的求解目标为使其联合概率最大化，即

NewImage

　　2. 如何求解问题？

　　　　对似然函数求导得到

　　　　算法表述在图上可以为

　　什么是多元正态分布（The Multivariate Normal Distribution）？

　　　　多元正态分布描述的是 n 维随机变量的分布情况,这里的μ变成了向量, σ也变成了矩阵Σ。写作𝛮(𝜇,𝛴)

　　　　其密度函数为：

NewImage

　　　　其中μ决定中心位置,Σ决定投影椭圆的朝向和大小

　　　　考虑x = [x_1, x_2]生成的图形是一个钟形函数

　　　　先来改变Σ的值，保持μ=0 恒定

　　　　当x_1和x_2不存在相关性 ------

NewImage

　　　　当x_1和x_2正相关 -------

NewImage

　　　　当x_1和x_2负相关 -------

NewImage

　　　　再来改变μ的值，保持Σ=I 恒定

NewImage

　　GDA和Logistic Regression有什么关系？

　　　　注释：简单的说Logistic Regression只要给一组数据，基本就可以分类，因为他只是“分类”而已。

　　　　　　　GDA不仅仅是分类，他需要先把样本拟合成K个高斯函数才能进行分类。

　　　　　　　有了上面两个说明，谁强谁弱显而易见了！

NewImage

　　　　如上图，首先我们有一些正负例（用O或者X表示在x轴上），分别对正负例建模，由于GDA要求的正负例分别服从高斯分布，画在图上就是两个钟形函数 p(x | y = 0) 和 p(x | y = 1)

有了这个分布，我们来看p(y = 1 | x)的概率表述，也就是计算给定样本之后的正例(y = 1)的分布，神奇的发现这是一个sigmoid function，和logistic regression的结果非常类似的sigmoid function！

　　 GDA和Logistic Regression 有什么关系呢？

　　　　答案是，虽然像，但是还是有本质区别的。

　　　　GDA中，假设特征服从高斯分布，那么其后验概率确实是logistic 类型的函数。

　　　　反过来，Logistic Regression得出的logistic 类型的函数，则不能推出它的特征是服从高斯分布的。

　　　　比如即使其特征服从泊松分布，它的后验也是logistic类型的。

　　　　事实上，只要特征是服从Generalized Linear Model的，后验都是logistic类型的。

NewImage

　　有了上面的分析，可以看出以下结论

　　　　Logistic Regression的适应能力更好，因为其对应特征可以服从很多分布，一般而言，只要不是特别不靠谱，都能得出一个比较可靠的模型。也就是模型更加鲁棒，对错误的模型假设更加不敏感。

　　　　而对于GDA，由于建立了很强的假设，如果特征不满足假设，那么模型效果就不会好。但如果特征真的满足了高斯分布的话，GDA可以得出非常靠谱的模型，并且训练非常有效率 --- 用很少的样本就可以训练出不错的模型。

三：朴素贝叶斯(Naive Bayes)

在GDA中，特征向量x是连续的实数向量，那么现在谈论一下当x是离散时的情况。

我们沿用对垃圾邮件进行分类的例子，我们要区分邮件是不是垃圾邮件。分类邮件是文本分类的一种应用

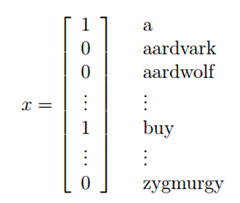
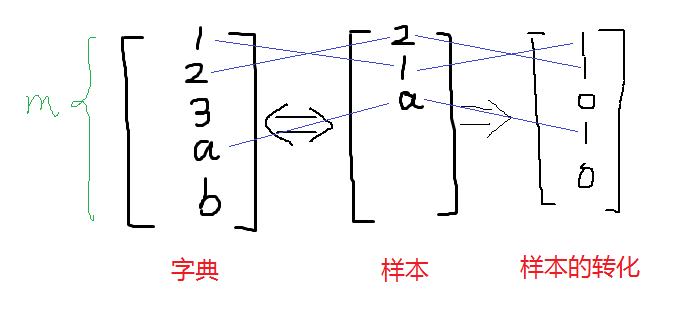
将一封邮件作为输入特征向量，与现有的字典进行比较，如果在字典中第i个词在邮件中出现，则x_i=1，否则x_i=0，所以现在我们假设输入特征向量如下：

注释：得有先验概率的数据去训练，参见《机器学习》周志华，P76页、P153页

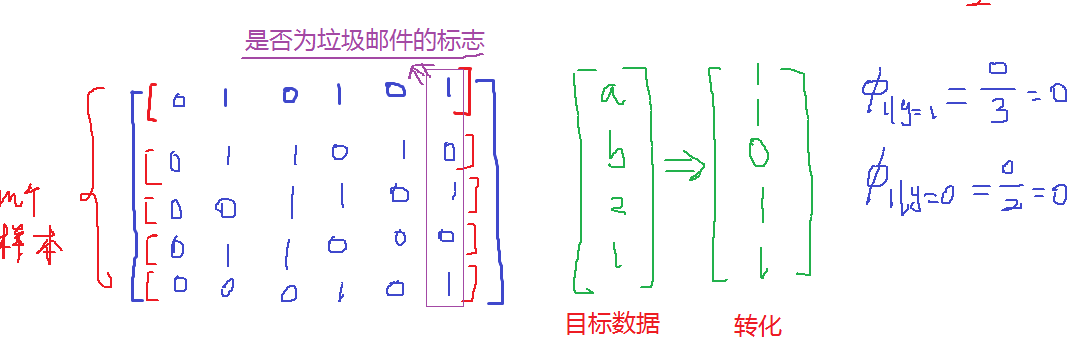
　　　　对样本数据进行处理：（重复的数据不增加，此算法只看有没有出现，有为1，无为0，出现十次也是1）

　　　　对目标数据进行处理：

　　　　对目标数据和样本数据进行对比求解：

　　　　　　　　注意这里求得前提是x=1,所以x为第三个特征的时候ø_x=0&y=1和ø_x=0&y=0都是不存在的！具体求解救不写了，上面说的那本书上有具体的例子！

选定特征向量后，现在要对p(x|y)进行建模：

注释：X_i代表样本中是否出现不好的词语，如果X_i=Dict[j]---->>>X_i=1 or X_i=0，y代表最终的输出，y=1表示垃圾邮件，y=0表示好的邮件。

假设字典中有50000个词，x ∈ {0, 1}⁵⁰⁰⁰⁰如果采用多项式建模，将会有2⁵⁰⁰⁰⁰种结果，2⁵⁰⁰⁰⁰-1维的参数向量，这样明显参数过多。所以为了对p(x|y)建模，需要做一个强假设，假设x的特征是条件独立的，这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).

解释：

如果有一封垃圾邮件(y=1),在邮件中出现buy这个词在2087这个位置它对39831这个位置是否出现price这个词都没有影响，也就是，我们可以这样表达p(x₂₀₈₇|y) = p(x₂₀₈₇|y, x₃₉₈₃₁)，这个和x₂₀₈₇and x₃₉₈₃₁ 相互独立不同，如果相互独立，则可以写为p(x₂₀₈₇) = p(x₂₀₈₇|x₃₉₈₃₁)，我们这里假设的是在给定y的情况下，x₂₀₈₇and x₃₉₈₃₁ 独立。