Group Normalization

Group Normalization

一. 论文简介

主要做的贡献如下（可能之前有人已提出）：

1. 类似BN的一种归一化，使用group进行归一化

二. 模块详解

2.1 BN的做法

1. 设 \(X\) 为输入的 \(batch\) 数据，\(\mu_B、\sigma_B\) 为当前 \(batch\) 的均值和方差，\(running\_u、runnnig\_\sigma\) 为滑动平均（全局）的均值和方差（初始化为0和1），\(\beta、\gamma\) 为梯度更新的均值和方差
2. 通过输入 \(X\) 计算当前均值和方差 \(\mu_B、\sigma_B\)
3. 使用 \(\mu_B、\sigma_B\) 归一化当前输入 \(X\)
4. 通过 \(moving\_momentum\) 和当前均值和方差更新全局均值和方差
5. 使用梯度更新的均值和方差还原输入的 \(X\)
6. 下面的图不全，仅仅包含一部分，请参考代码

# 参考https://blog.csdn.net/weixin_40123108/article/details/83509838
def batch_norm_1d(x, gamma, beta, is_training, moving_mean, moving_var, moving_momentum=0.1):
    eps = 1e-5
    x_mean = torch.mean(x, dim=0, keepdim=True) # 保留维度进行 broadcast
    x_var = torch.mean((x - x_mean) ** 2, dim=0, keepdim=True)
    if is_training:
        x_hat = (x - x_mean) / torch.sqrt(x_var + eps)
        moving_mean[:] = moving_momentum * moving_mean + (1. - moving_momentum) * x_mean
        moving_var[:] = moving_momentum * moving_var + (1. - moving_momentum) * x_var
    else:
        x_hat = (x - moving_mean) / torch.sqrt(moving_var + eps)
    return gamma.view_as(x_mean) * x_hat + beta.view_as(x_mean)

---

2.2 GN的做法

• 整体思想看下图一目了然
• 论文给的代码中没有滑动平均，由于和 \(Batch\) 无关，所以不需要滑动平均。因为如果使用滑动平均，不如直接在 \(batch\) 上平均，反正也算是多个数（见下图四，在N上取平均近似等于滑动平均）

# TF 版本源论文
def GroupNorm(x, gamma, beta, G, eps=1e−5):
    # x: input features with shape [N,C,H,W]
    # gamma, beta: scale and offset, with shape [1,C,1,1] # G: number of groups for GN
    N, C, H, W = x.shape
    x = tf.reshape(x, [N, G, C // G, H, W])
    mean, var = tf.nn.moments(x, [2, 3, 4], keep dims=True) x = (x − mean) / tf.sqrt(var + eps)
    x = tf.reshape(x, [N, C, H, W]) return x ∗ gamma + beta

# pytorch版本:https://zhuanlan.zhihu.com/p/56219719
import numpy as np
import torch
import torch.nn as nn


class GroupNorm(nn.Module):
    def __init__(self, num_features, num_groups=32, eps=1e-5):
        super(GroupNorm, self).__init__()
        self.weight = nn.Parameter(torch.ones(1,num_features,1,1))
        self.bias = nn.Parameter(torch.zeros(1,num_features,1,1))
        self.num_groups = num_groups
        self.eps = eps

    def forward(self, x):
        N,C,H,W = x.size()
        G = self.num_groups
        assert C % G == 0

        x = x.view(N,G,-1)
        mean = x.mean(-1, keepdim=True)
        var = x.var(-1, keepdim=True)

        x = (x-mean) / (var+self.eps).sqrt()
        x = x.view(N,C,H,W)
        return x * self.weight + self.bias

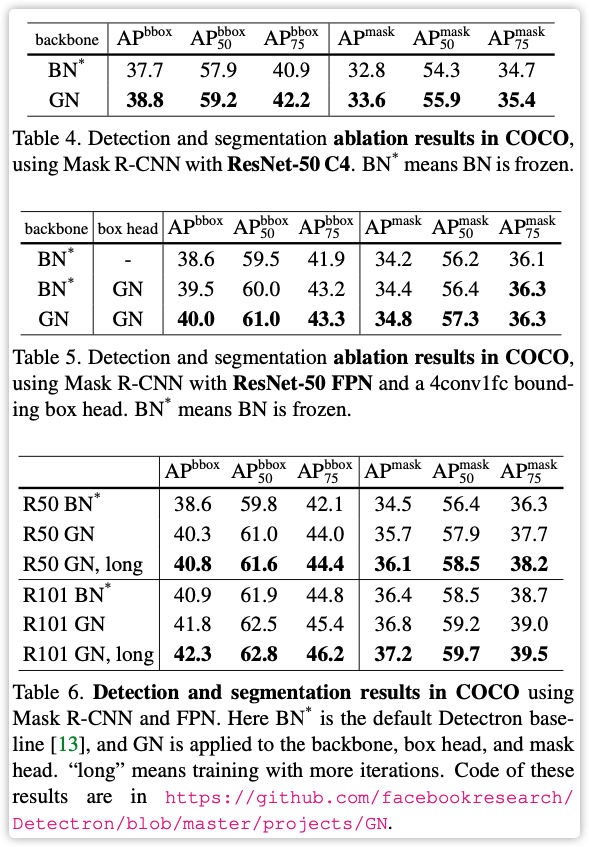
• 看论文试验，针对大网络小 \(batch\) 有作用，正常网络单GPU大于32还是使用BN比较好

三. 参考文献

• 原始论文
• BN code
• GN code