Distribution-Aware Coordinate Representation for Human Pose Estimation
Distribution-Aware Coordinate Representation for Human Pose Estimation
一. 论文简介
设计gaussian heatmap的后处理,获得更精确的位置坐标
主要做的贡献如下(可能之前有人已提出):
- encode使用non-bias生成heatmap
- decode使用gaussian函数梯度求取

二. 模块详解
2.1 整体结构介绍
论文思想比较简单,整体进行概括
- 编码部分不进行说明,现在都是这样做的。
- 解码部分是此论文核心
- 最原始的做法是直接argmax即可,以下是部分论文进行改进的,\(m\) 是最大值点,\(s\) 是第二大值点,然后进行加权得到最终位置 \(p\)
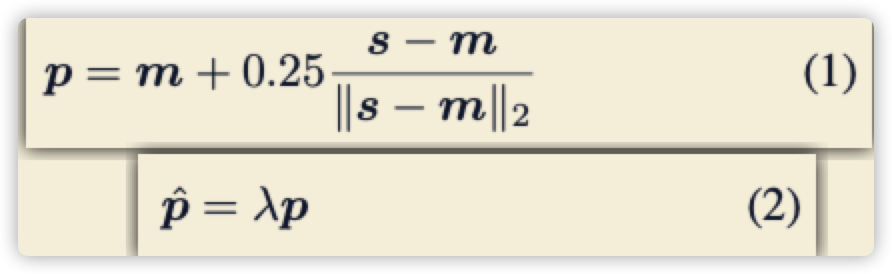
- 改进后看下图
生成label的时候我们直接把每个点强制进行高斯分布形成heatmap,如果\(center=(15.6,15.6)\),那么生成的图\(center=(16,16)=0.999\)
直接进行找最大值的后果(理想情况),获得坐标\(center=(16,16)\)
如何进行拟合到原始坐标?
假设预测的图符合高斯分布(理想情况),那么最大值点梯度为0,我们可以使用这两个条件进行反向求解,其中 \(\sigma\) 是已知的(生成label相同),直接聚类拟合即可。
这种方式计算量太大,不利于后处理?
先找到当前的最大值坐标,假设为 \(m\) 点,设实际的中心点为 \(u\) ,将二维高斯按照泰勒展开,得到下下图公式\((7)\),\(u\) 点导数为0得到公式\((6)\),那么我们可以将公式\((7)\)求导数化解为公式\((9)\) ,其中公式\((8)\)为数字图像的二阶倒数(hessian矩阵)。
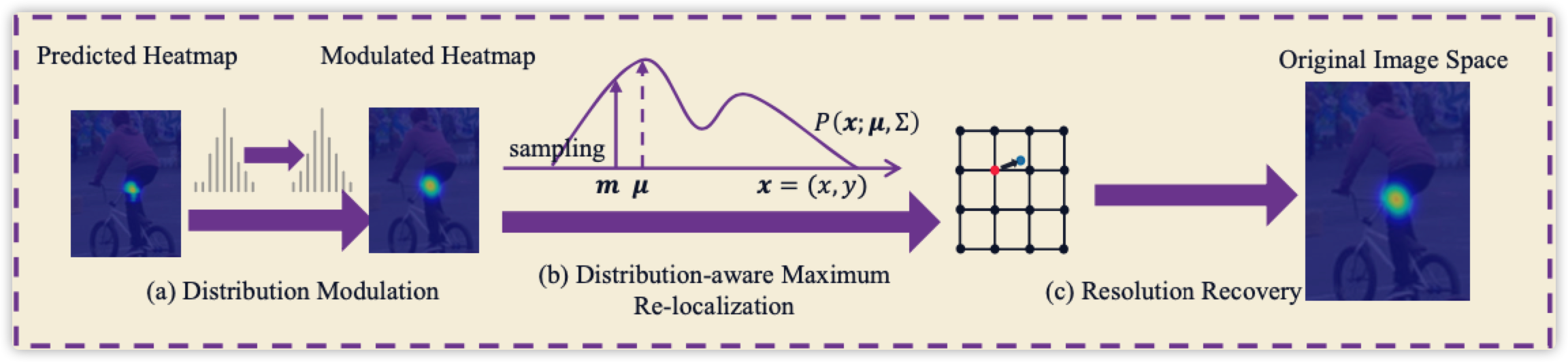

还有一个值得注意的地方,上面公式都是理想情况,如果不理想呢?
先将预测的heatmap进行高斯滤波,从下图\((a)\)转化为\((b)\),方式就是公式\((10)\),最后进行一个归一化,其中max为直接输出heatmap的最大值,也就是公式\((11)\)所示。


三. 缺点
- 假设条件是凸函数,很多情况矩阵不是正定的
-------------------------------------------
个性签名:衣带渐宽终不悔,为伊消得人憔悴!
如果觉得这篇文章对你有小小的帮助的话,记得关注再下的公众号,同时在右下角点个“推荐”哦,博主在此感谢!


