卷积神经网络（CNN）基础

Padding and stride

 

一个N*N的图像，使用f*f的卷积核，会得到（n-f+1）*（n-f+1）的大小

但是边缘的图像 使用了一次，而且整个图像缩小了

因此，可以增加一圈padding，假设增加的padding 的长度为p

会得到（n+2p-f+1）*（n+2p-f+1）的图像

 

通常由两种卷积方式

“Valid”：不填充

“Same”：填充2p，使得输入输出相同大小

（n+2p-f+1）==n→2p+1-f==0→p=（f-1）/2

所以f通常情况下为奇数

 

 

 

如果加入了Stride

那么输出的图像大小就变成[（n+2p-f）/s+1]* [（n+2p-f）/s+1]

//n+2p-f 剩余长度 /s 移动个数 +1 初始位置

如果除法（n+2p-f）/s不是一个整数，一般向下取整数，即放弃最后一个不完全的框

 

三维卷积

计算方式：对应位置的数字相乘，将乘积的和放在对应的位置

可以为三个通道的过滤器，设置不同的过滤器，但是过滤器的通道数必须和原图一样

 

 

 

 

 

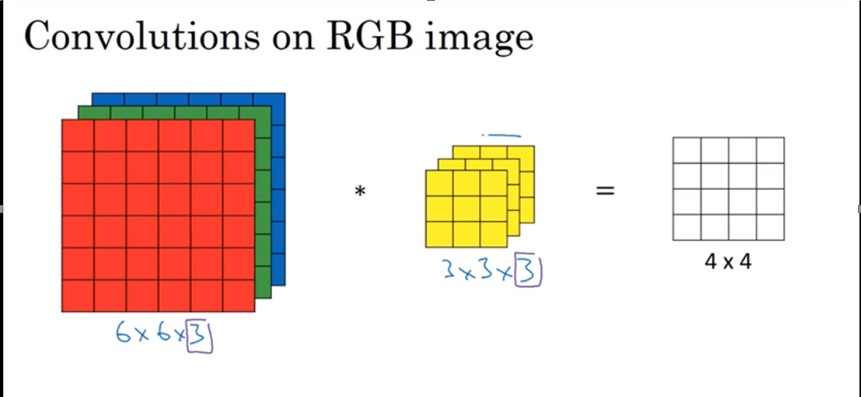
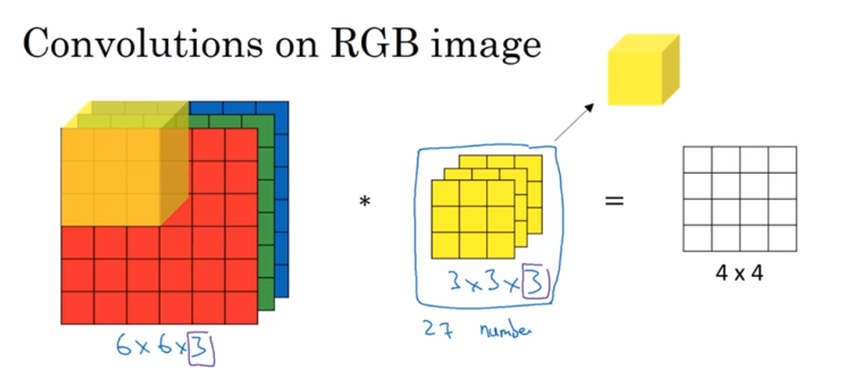
我们可以设置多个过滤器，例如相对Red层即检测垂直边界，又检测水平边界，那么我们可以选择通过两个立体过滤器，如下图中，橙色和黄色为不同的过滤器，将结果组合，就得到下一层的输入

 

 

 

Summary：

N*N*n_channels    *    f*f*n_channels    →  （n-f+1）*（n-f+1）*number of n_channels

6*6*3                  3*3*3                  4     *  4    *     2

 

单层卷积网络

 

 

 

Input: N_h^[l-1]* N_w^[l-1]*N_c^[l-1]  width*height*channels_num in layer l-1

Output: N_h^[l]* N_w^[l]*N_c^[l]  width*height*channels_num in layer l

Each filter is: f^[l]*f^[l]*N_c^[l-1] f*f* channels_num in layer l-1

Activations: a^[l]= N_h^[l]* N_w^[l]*N_c^[l]  A^[l]= m*N_h^[l]* N_w^[l]*N_c^[l]

Weight: Each filter * filter_num f^[l]*f^[l]*N_c^[l-1]*N_c^[l]

Bias: (1,1,1,N_c^[l]) 横向排列组合的一排小立方体

为什么使用卷积

卷积可以减少参数量

参数共享

同一个卷积核可以在不同区域中使用，例如垂直边界卷积核可以在多次使用

稀疏链接

每一层中的输出仅仅和上一层中的几个参数相关，例如一个3*3的filter仅仅涉及9个参数

 

 

池化

特殊的过滤器，对一个块内的信息做不同的操作，eg，max、average，

Hyperparameter超参：filter size、stride

全连接

 

 

 

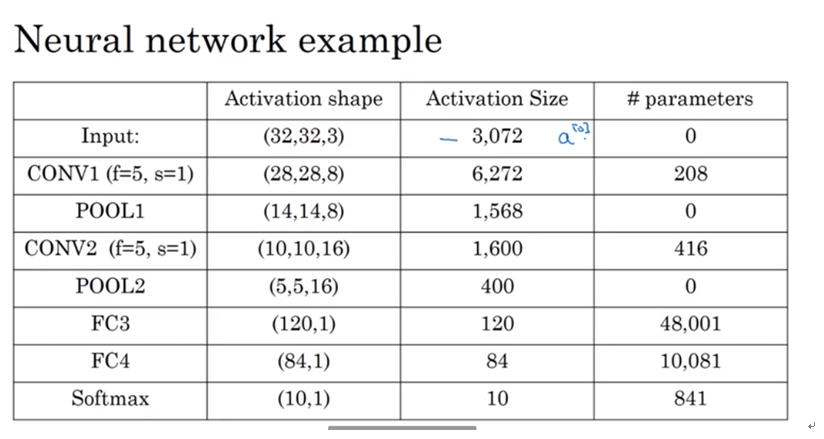
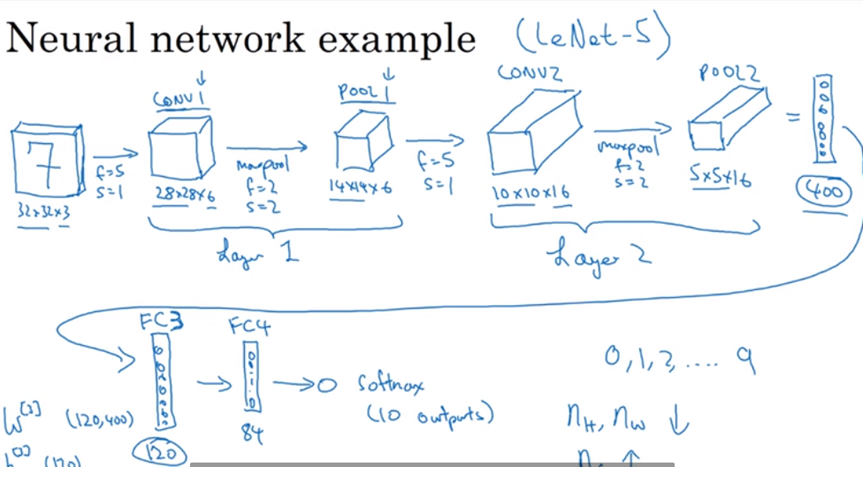
参数=filter_size*filter_size+bias || Activation size^(L-1)*Actication size^(L)+bias  偏置一般就是1