Android -- 贝塞尔曲线公式的推导和简单使用

1，最近看了几个不错的自定义view，发现里面都会涉及到贝塞尔曲线知识，深刻的了解到贝塞尔曲线是进阶自定义view的一座大山，so，今天先和大家来了解了解。

2，贝塞尔曲线作用十分广泛，简单举几个的栗子:

　　QQ小红点拖拽效果
　　360火箭发射
　　加入购物车动画
　　一些炫酷的下拉刷新控件
　　阅读软件的翻书效果
　　一些平滑的折线图的制作
　　很多炫酷的动画效果

　　这么多好看的效果，难道不想自己也写一个吗。。。。

• 理解贝塞尔曲线的原理　

　　贝塞尔曲线是用一系列点来控制曲线状态的，我将这些点简单分为两类：数据点、控制点。通过调整控制点，贝塞尔曲线形状会发生变化。

　　数据点：确定曲线的起始和结束位置
　　控制点：确定曲线的弯曲程度

• 一阶曲线原理

  一阶曲线是没有控制点的，仅有两个数据点(A 和 B)，最终效果一个线段。

　　

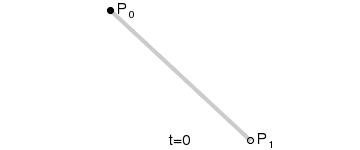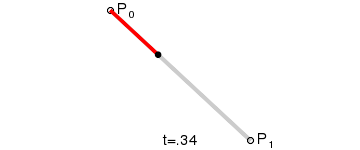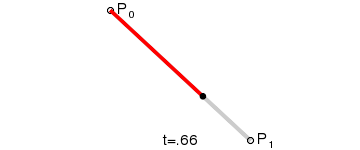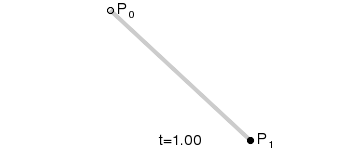
　　一阶公式如下：

　　

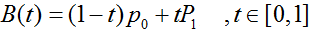
• 二阶曲线原理

　　二阶曲线由两个数据点(A 和 C)，一个控制点(B)来描述曲线状态，大致如下：

　　　　

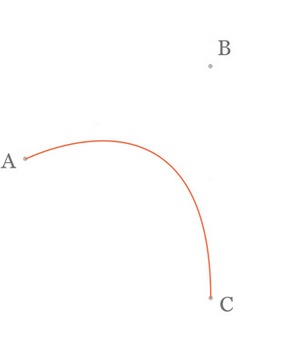
　　那么ac之间的红线是怎么生成的呢，让我们了解一下

　　

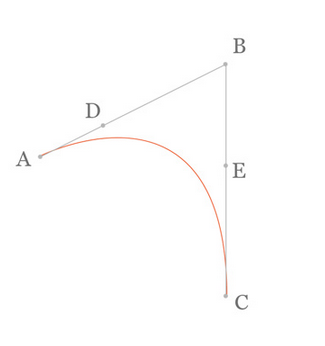
　　在AB线段和BC线段分别去D、E两点，且满足条件

　　　　

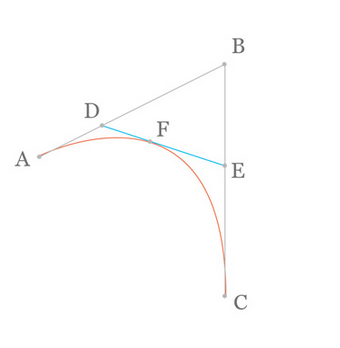
　　连接DE，取点F，使得: ，这样获取到的点F就是贝塞尔曲线上的一个点，动态图如下：

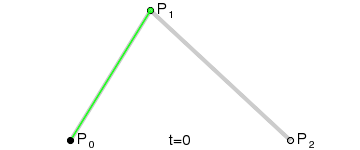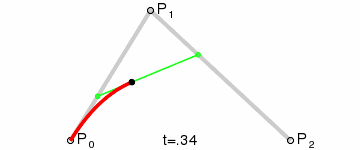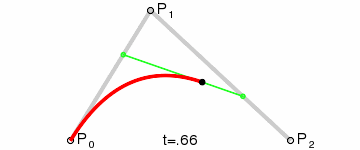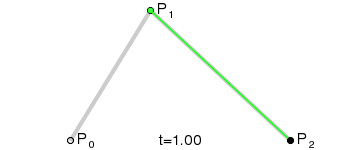
　　二阶公式如下：

　　

• 三阶曲线原理

  三阶曲线由两个数据点(A 和 D)，两个控制点(B 和 C)来描述曲线状态

 　　　　

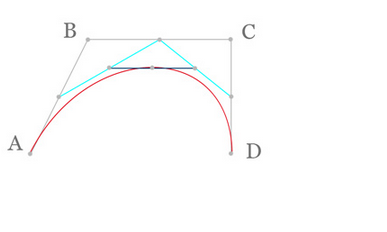
　　动态图如下：

　　三阶公式如下：

　　

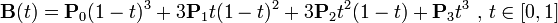
• 四阶曲线

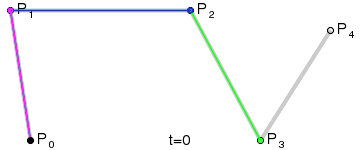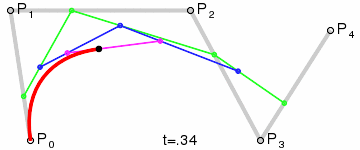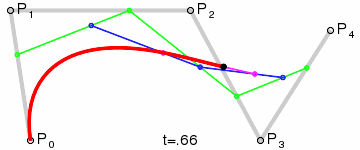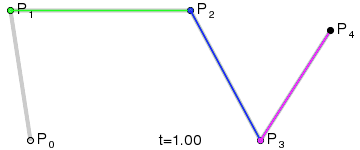
• 五阶曲线

 　　通用公式：

　　

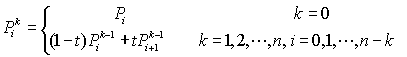
3，公式推导

　　由于博客园的编辑器无法编写高数公式，所以我这里就在纸上写了，如果有点看不到的话可以把图片下下来再放大看看（见谅）

 　　

　　

　　

 4，实现简单的小例子

　　在我们Android中Path类中其实是有已经封装好了关于贝塞尔曲线的函数的

　　//二阶贝赛尔  
　　public void quadTo(float x1, float y1, float x2, float y2)  
　　public void rQuadTo(float dx1, float dy1, float dx2, float dy2)  
　　//三阶贝赛尔  
　　public void cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)  
　　public void rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3) 

• quadTo（）方法

　　让我们先来看一下源码

/**
     * Add a quadratic bezier from the last point, approaching control point
     * (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for
     * this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the control point on a quadratic curve
     * @param y1 The y-coordinate of the control point on a quadratic curve
     * @param x2 The x-coordinate of the end point on a quadratic curve
     * @param y2 The y-coordinate of the end point on a quadratic curve
     */
    public void quadTo(float x1, float y1, float x2, float y2) {
        isSimplePath = false;
        native_quadTo(mNativePath, x1, y1, x2, y2);
    }

　　从源码的注释上我们可以得到的信息如下：参数中(x1,y1)是控制点坐标，(x2,y2)是终点坐标 。　　

　　大家可能会有一个疑问：有控制点和终点坐标，那起始点是多少呢？ 整条线的起始点是通过Path.moveTo(x,y)来指定的，而如果我们连续调用quadTo()，前一个quadTo()的终点，就是下一个quadTo()函数的起点；如果初始没有调用Path.moveTo(x,y)来指定起始点，则默认以控件左上角(0,0)为起始点；

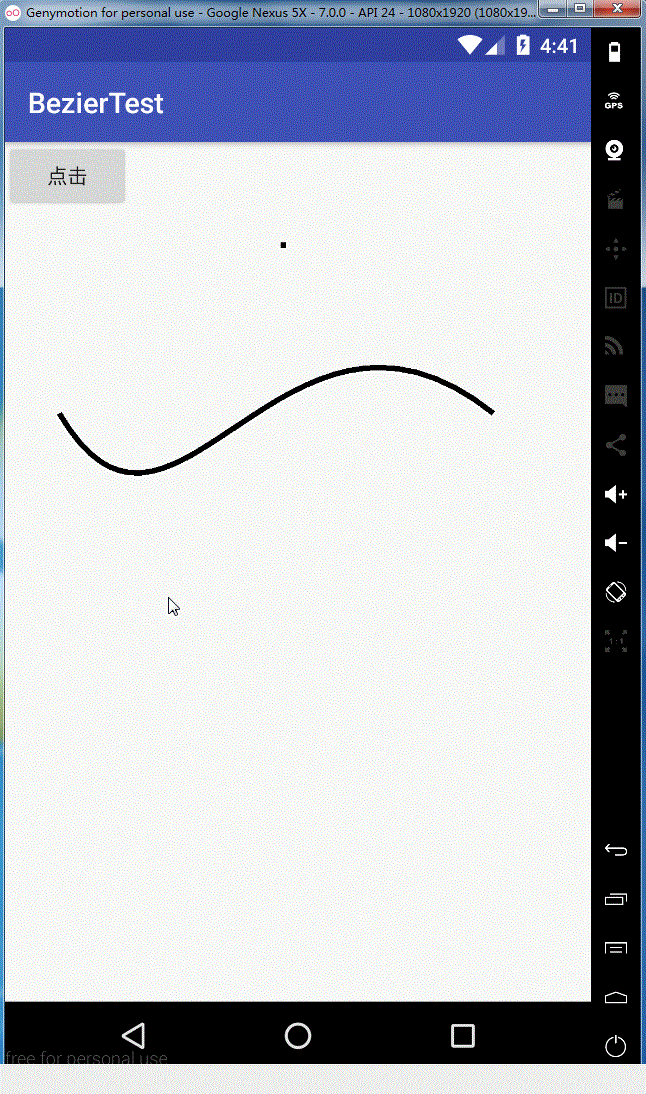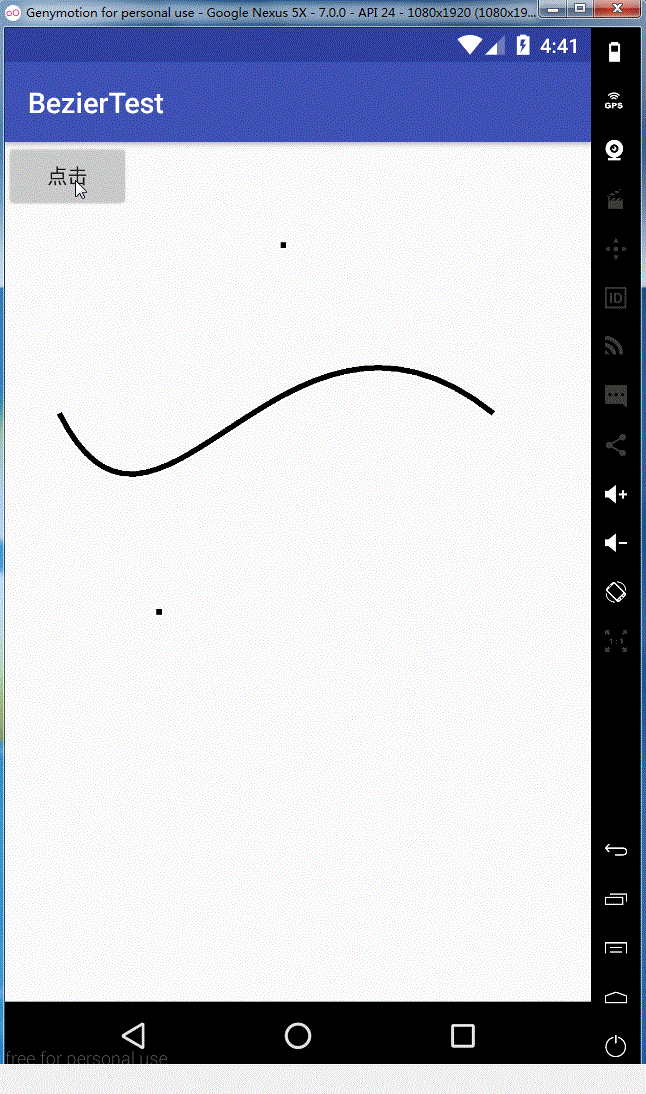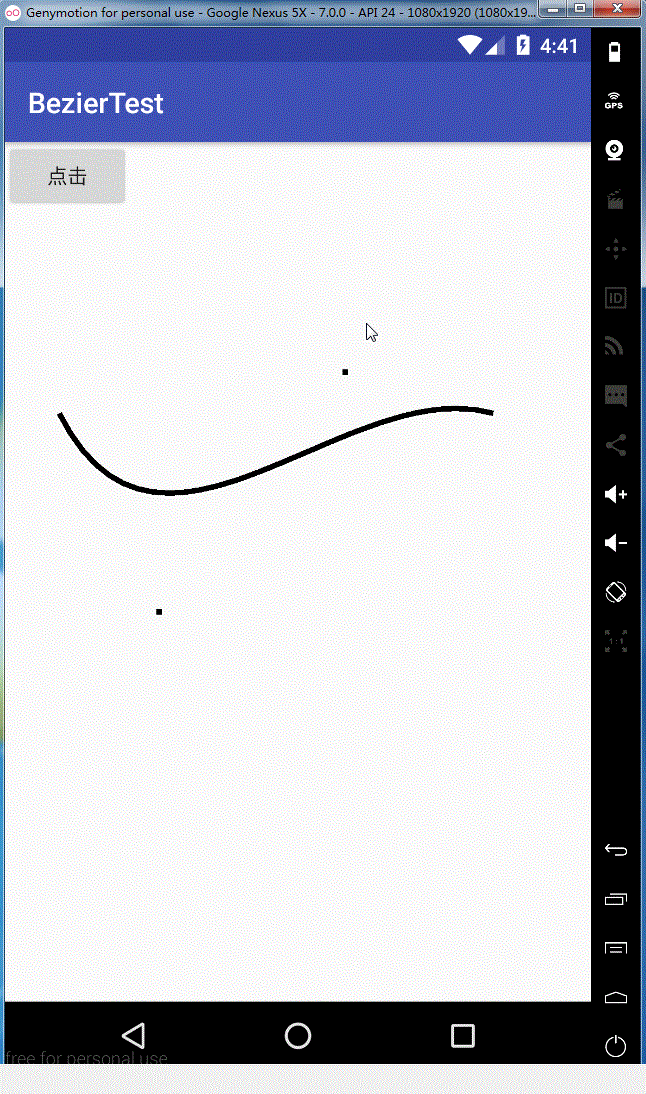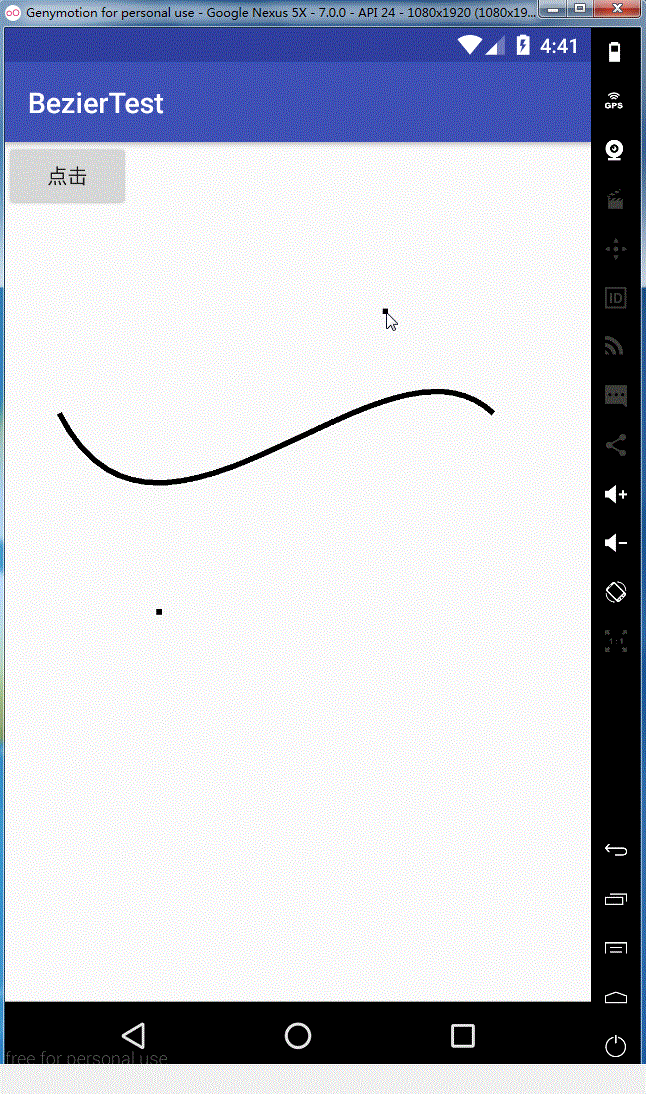
　　我们简单的写一下demo，通过我们点击屏幕来动态的获取点击屏幕的坐标，然后将其设置成贝二阶塞尔曲线的控制点，代码很简单

package com.qianmo.beziertest.view;


import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.Point;
import android.support.annotation.Nullable;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;

import com.qianmo.beziertest.R;

/**
 * Created by Administrator on 2017/3/30 0030.
 * E-Mail：543441727@qq.com
 */

public class MyView extends View {

    private Point controlPoint = new Point(200, 200);

    public MyView(Context context) {
        super(context);
    }

    public MyView(Context context, @Nullable AttributeSet attrs) {
        super(context, attrs);
    }

    public MyView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);

        Paint paint = new Paint();
        paint.setStyle(Paint.Style.STROKE);
        paint.setColor(Color.BLACK);
        paint.setStrokeWidth(10);

        Path path = new Path();
        path.moveTo(100, 500);
        path.quadTo(controlPoint.x, controlPoint.y, 700, 500);
        //绘制路径
        canvas.drawPath(path, paint);
        //绘制辅助点
        canvas.drawPoint(controlPoint.x,controlPoint.y,paint);

    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()) {
            case MotionEvent.ACTION_MOVE:
                controlPoint.x = (int) event.getX();
                controlPoint.y = (int) event.getY();
                invalidate();
                break;
        }
        return true;
    }
}

　　效果图如下：

• rQuadTo（）

　　先来看一下它的源码，代码如下：

/**
     * Same as quadTo, but the coordinates are considered relative to the last
     * point on this contour. If there is no previous point, then a moveTo(0,0)
     * is inserted automatically.
     *
     * @param dx1 The amount to add to the x-coordinate of the last point on
     *            this contour, for the control point of a quadratic curve
     * @param dy1 The amount to add to the y-coordinate of the last point on
     *            this contour, for the control point of a quadratic curve
     * @param dx2 The amount to add to the x-coordinate of the last point on
     *            this contour, for the end point of a quadratic curve
     * @param dy2 The amount to add to the y-coordinate of the last point on
     *            this contour, for the end point of a quadratic curve
     */
    public void rQuadTo(float dx1, float dy1, float dx2, float dy2) {
        isSimplePath = false;
        native_rQuadTo(mNativePath, dx1, dy1, dx2, dy2);
    }

　　从上面的方法注释我们可以看到，这是一个相对坐标，具体参数意思如下：

dx1:控制点X坐标，表示相对上一个终点X坐标的位移坐标，可为负值，正值表示相加，负值表示相减；
dy1:控制点Y坐标，相对上一个终点Y坐标的位移坐标。同样可为负值，正值表示相加，负值表示相减；
dx2:终点X坐标，同样是一个相对坐标，相对上一个终点X坐标的位移值，可为负值，正值表示相加，负值表示相减；
dy2:终点Y坐标，同样是一个相对，相对上一个终点Y坐标的位移值。可为负值，正值表示相加，负值表示相减；

　　这里举个例子，假如我们上一个终点坐标是(300,400)那么利用rQuadTo(100,-100,200,100)； 得到的控制点坐标是（300+100,400-100）即(500,300) 同样，得到的终点坐标是(300+200,400+100)即(500,500)，这个方法和quadTo（）方法没什么区别，所以就不写Demo写了

• cubicTo（）

　　这是Android的三阶贝塞尔曲线方法，先来看一下每一参数的意义

/**
     * Add a cubic bezier from the last point, approaching control points
     * (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been
     * made for this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the 1st control point on a cubic curve
     * @param y1 The y-coordinate of the 1st control point on a cubic curve
     * @param x2 The x-coordinate of the 2nd control point on a cubic curve
     * @param y2 The y-coordinate of the 2nd control point on a cubic curve
     * @param x3 The x-coordinate of the end point on a cubic curve
     * @param y3 The y-coordinate of the end point on a cubic curve
     */
    public void cubicTo(float x1, float y1, float x2, float y2,
                        float x3, float y3) {
        isSimplePath = false;
        native_cubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
    }

　　从上面源码可以看到参数(x1,y1)是第一个控制点坐标，(x2,y2)是第二个控制点坐标，(x3，y3)是终点坐标。

　　整条线的起始点是通过Path.moveTo(x,y)来指定的，而如果我们连续调用cubicTo()，前一个cubicTo()的终点，就是下一个cubicTo()函数的起点；如果初始没有调用Path.moveTo(x,y)来指定起始点，则默认以控件左上角(0,0)为起始点；和我们的quadTo（）方法一样。

　　下面也是通过一个小例子给大家看一下效果，和二阶贝塞尔曲线一样，就是多了一个控制点代码如下：

package com.qianmo.beziertest.view;


import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.graphics.Point;
import android.support.annotation.Nullable;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;

/**
 * Created by wangjitao on 2017/3/30 0030.
 * E-Mail：543441727@qq.com
 */

public class MyView1 extends View {

    private Point controlPointOne = new Point(200, 200);
    private Point controlPointTwo = new Point(500, 200);

    private boolean isControlPointTwo ;

    private Paint paintBezier;
    private Paint paintLine;

    public MyView1(Context context) {
        this(context, null);
    }

    public MyView1(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public MyView1(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);

        paintBezier = new Paint();
        paintBezier.setStyle(Paint.Style.STROKE);
        paintBezier.setColor(Color.BLACK);
        paintBezier.setStrokeWidth(10);


        paintLine = new Paint();
        paintLine.setStyle(Paint.Style.STROKE);
        paintLine.setColor(Color.RED);
        paintLine.setStrokeWidth(3);

    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);


        Path path = new Path();
        path.moveTo(100, 500);
        path.cubicTo(controlPointOne.x, controlPointOne.y,controlPointTwo.x, controlPointTwo.y, 900, 500);
        //绘制路径
        canvas.drawPath(path, paintBezier);
        //绘制辅助点
        canvas.drawPoint(controlPointOne.x, controlPointOne.y, paintBezier);
        canvas.drawPoint(controlPointTwo.x, controlPointTwo.y, paintBezier);
        //绘制连线
//        canvas.drawLine(100, 500, controlPointOne.x, controlPointOne.y, paintLine);
//        canvas.drawLine(900, 500, controlPointOne.x, controlPointOne.y, paintLine);
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()) {
            case MotionEvent.ACTION_MOVE:
                if (isControlPointTwo){
                    controlPointOne.x = (int) event.getX();
                    controlPointOne.y = (int) event.getY();
                }else {
                    controlPointTwo.x = (int) event.getX();
                    controlPointTwo.y = (int) event.getY();
                }
                invalidate();
                break;
        }
        return true;
    }


    public boolean isControlPointTwo() {
        return isControlPointTwo;
    }

    public void setControlPointTwo(boolean controlPointTwo) {
        isControlPointTwo = controlPointTwo;
    }
}

　　效果如下：

　　同理rCubicTo，这里就不给大家解释了

　　ok，本篇基本上把贝塞尔的基础知识都了解完了，明天开始试着来撸撸轮子，感觉一大波好看的动画满天飞的控件在等着我们（邪恶脸）。See You Next Time。。。。