| 预测值 | |||
| 正例 | 负例 | ||
| 真实值 | 正例 | 真正例(A) | 假负例(B) |
| 负例 | 假正例(C) | 真负例(D) | |
| 预测值 | |||
| 正例 | 负例 | ||
| 真实值 | 正例 | TP | FN |
| 负例 | FP | TN | |
模型测试一般用四个指标来衡量:
准确率(Accuracy): 提取出的正确样本数/总样本数
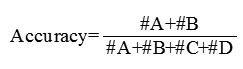
召回率(Recall):正确的正例样本数/样本中的正例样本数,也定义为查全率
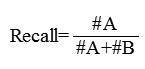
精准率(Precision):正确的正例样本数/预测为正例的样本数,也定义为查准率
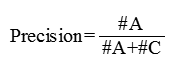
F值:等于召回率和精准率的调和平均值
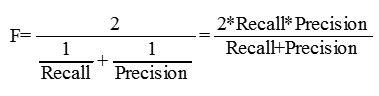
这里需要注意的是召回率和精准率的关系是互斥的,其原因为:
1.对于召回率而言,其分母是固定的,是真实值中正例的数目,我们希望召回率(即查全率)是越高越好的,其极限条件就是当所有值都认定为是正例时,召回率就为1,但是这样做的缺点是无法区分正例和负例,比如,正例为患病人数,负例为健康人数,如果召回率为1,即认为测试样本中的所有人都是有病的,显然这样做是不合理的;
2.如果我们希望召回率增加,即测值中的正例数是增加的,如下表:(其中正例表示患病,负例表示健康,目的是在找出样本中的患病人数)
情况1
| 预测值 | |||
| 正例:70 | 负例:30 | ||
| 真实值 | 正例:80 | TP:60 | FN:20 |
| 负例:20 | FP:10 | TN:10 | |
召回率:3/4(查全率)
精准率:6/7(查准率)
情况2
| 预测值 | |||
| 正例:75 | 负例:25 | ||
| 真实值 | 正例:80 | TP:64 | FN:10 |
| 负例:20 | FP:11 | TN:15 | |
召回率:64/80
精准率:64/75
3.由上面的分析可得,由于真正例和假正例的比例是不变的,当预测值中正例样本数增加时,真正例和假正例的值都会增加,但是分子对于分母差了一个假正例的数值,所以在此情况下,召回率是增加的,即查全率增加,但是差准率相应降低。
简单理解就是,认为多数人是患病的,那么查全的概率是增加的,但是都多数人结果会造成查准的降低。




