数据结构中树的基本概念

整理下数据结构中相关树的基本概念

 

树：树（Tree）是 n(n>=0) 个结点的有限集。树型结构是一类重要的非线性数据结构。

在任意一棵非空树中 ，

1、有且仅有一个特定的称为根（Root）的结点。

2、当 n>1 时，其余结点分为m(m>0)个互不相交的有限集，其中每一个集合本身又是一颗树，并且称为根的子树（SubTree）。

 

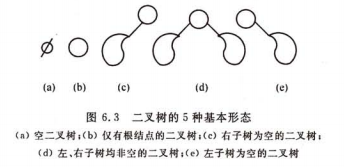
二叉树：二叉树是一树树形结构，它的特点是每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树的5种基本形态

       　　　　　　　　　　

 

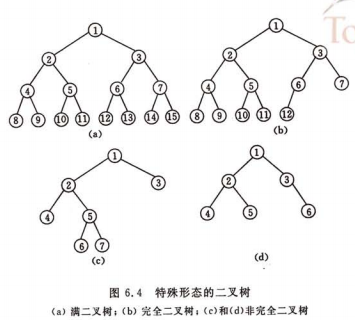
满二叉树 和 完全二叉树 是两种特殊形态的二叉树

满二叉树：一棵深度为k且有 2的k字幂-1 个结点的二叉树称为满二叉树。特点：每一层上的结点数都是最大的结点数。

完全二叉树：可以对满二叉树的结点进行连续编号，约定编号从根结点起，自上而下，自左而右。深度为k的，有n个结点的二叉树，

当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称之为完全二叉树。（注：很多书中的完全二叉树定义不一样）

　　　　　　　　　　　　　　

 

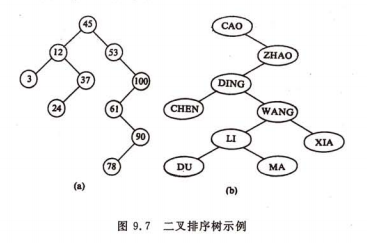
二叉排序树（又称二叉查找树）：

或者是一棵空树，或者是具有下列性质的二叉树：

1、若它的左子树不为空，则左子树上的所有结点的值均小于它的根结点的值。

2、若它的右子树不为空，则右子树上的所有结点的值均大于它的根结点的值。

3、它的左、右子树也分别为二叉排序树。

　　　　　　　　　　

 

 

 

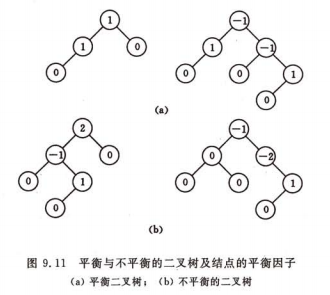
平衡二叉树（Balanced Binary Tree 又称AVL树，全称 Adelson-Velsky-Landis Tree，根据发明人的名字命名）：

或者是一棵空树，或者是具有下列性质的二叉树：

1、它的左子树和右子树都是平衡二叉树。

2、左子树和右子树的深度之差的绝对值不超过1。

平衡二叉树具有二叉查找树的全部特性。

若将二叉树上结点的平衡因子BF(Balance Factor) 定义为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有结点的平衡因子只可能是-1、0和1。

只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

　　　　　　　　　　　　

 

 

 

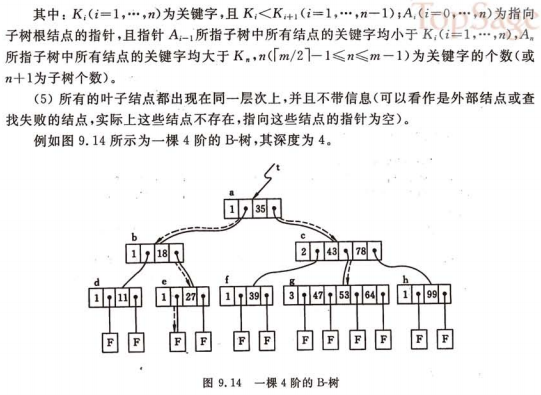
B-Tree （称B树，-减号是连接符）：是一种平衡的多路查找树（是m叉树，不只是二叉）。

一棵m阶的B树，或者为空树，或为满足下列特性的m叉树：

1、树中每个结点至多有m棵子树

2、若根结点不是叶子结点，则至少有两棵子树

3、除根结点之外的所有非终端结点至少有 m/2上取整 个子结点

4、所有的非终端结点中包含下列信息数据（n,A0,K1,A1,K2,A2,...,Kn,An）

　　　　　　　　

 

 

 

B-树的查找分析：

在B-树上查找包含两种基本操作：

1、在B-树中找结点。

2、在结点中找关键字。

由于B-树通常存储在磁盘上，则前一查找操作是在磁盘上进行的，而后一查找操作是在内存中进行的，即在磁盘上找到指针p所指结点后，

先将结点中的信息读入内存，然后再利用顺序查找或折半查找查询等于K的关键字。显然，在磁盘上进行一次查找比在内存中进行一次查找耗费时间多得多，

因此，在磁盘上进行查找的次数、即待查关键字所有的结点在B-树上的层次数，是决定B-树查找效率的首要因素。

 

 

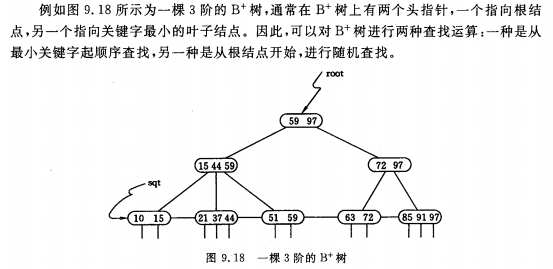
B+Tree （B+树，+加号应该是在右上角）：B+树是应文件系统所需而出的一种B树的变型树。一棵B+树 和 m阶B树的差异在于：

1、有n棵子树的结点中含有n个关键字

2、所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

3、所有的非终端结点可以看成是索引部分，结点中仅含有其子树（根结点）中的最大（或者最小）关键字。