神经网络

目录

• 神经元模型
• 感知机
• BP算法(反向传播算法)
• 扩展

神经元模型

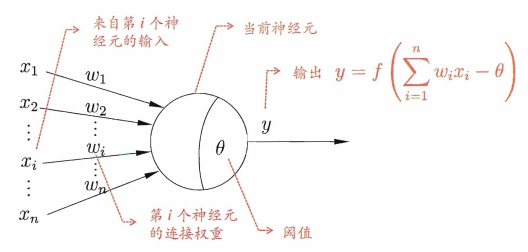
如上图，神经元接收到来自\(n\)个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出。

感知机

对训练样例\((x,y)\)，若当前感知机的输出为\(\hat{y}\)，则感知机权重将这样调整：

\[w_i \leftarrow w_i +\Delta w_i,\\ \Delta w_i=\eta(y-\hat{y})x_i \]

其中，\(\eta\in (0,1)\)称为学习率，\(w_i\)为权重。若感知机对训练样例\((x,y)\)预测正确，则感知机不发生变化；否则将根据错误的程度进行权重调整。

多层前馈神经网络：每层神经元与下一层神经元互连，神经元之间不存在同层连接，也不存在跨层连接。

神经网络的学习过程，就是根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值。

BP算法(反向传播算法)

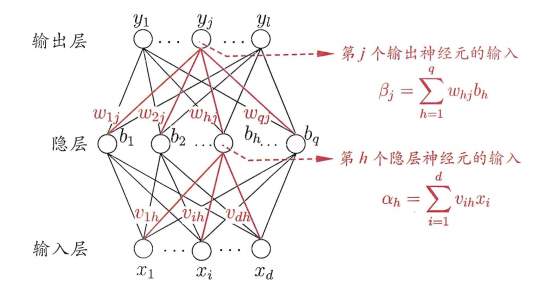
给定训练集\(D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\},\ x_i\in R^d,\ y_i\in R_l\)，即输入示例由\(d\)个属性描述，输出\(l\)维实值向量。

对训练集，假定神经网络的输出为\(\hat{y_k}=(\hat{y}_1^k,\hat{y}_2^k,\cdots,\hat{y}_l^k)\)，即

\[\hat{y}_j^k=f(\beta_j-\theta_j) \]

其中，\(\theta_j\)表示输出层第\(j\)个神经元的阈值。

均方误差为：

\[E_k=\frac{1}{2}\sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2 \]

BP是一个迭代算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计。BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，有

\[\Delta w_{hj}=\eta \frac{\partial E_k}{\partial w_{hj}} \]

由于\(w_{hj}\)先影响到第\(j\)个输出层神经元的输入值\(\beta_j\)，再影响到其输出值\(\hat{y}_j^k\)，然后影响到\(E_k\)，有：

\[\frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat{y}_j^k}\cdot \frac{\hat{y}_j^k}{\partial \beta_j}\cdot \frac{\beta_j}{\partial w_{hj}} \]

对于Sigmoid函数，有\(f'(x)=f(x)(1-f(x))\)
其中，

\[g_j=-\frac{\partial E_k}{\partial \hat{y}_j^k}\cdot \frac{\hat{y}_j^k}{\partial \beta_j}\\ =-(\hat{y}_j^k-y_j^k)f'(\beta_j-\theta_j)\\ =\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k)\]

\[\frac{\beta_j}{\partial w_{hj}}=b_h \]

因此，$$\Delta w_{hj}=\eta g_j b_h$$

类似可得：

\[\Delta \theta_j=-\eta g_j\\ \Delta v_{ih}=\eta e_h x_i\\ \Delta \gamma_h=-\eta e_h\]

其中，

\[e_h=-\frac{\partial E_k}{\partial b_h}\cdot \frac{\partial b_h}{\partial \alpha_h}\\ =-\sum_{j=1}^l \frac{\partial E_k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial b_h}f'(\alpha_h - \gamma_h)\\ =\sum_{j=1}^lw_{hj}g_jf'(\alpha_h - \gamma_h)\\ =b_h(1-b_h)\sum_{j=1}^lw_{hj}g_j\]

BP算法的目标是要最小化训练集\(D\)上的累计误差：$$E=\frac{1}{m}\sum_{k=1}^mE_k$$

标准BP算法：每次仅针对一个训练样例更新连接权和阈值。

BP神经网络经常遭遇过拟合，其训练误差持续降低，但测试误差却可能上升。解决策略：

1. “早停”(early stopping)：将数据分成训练集和验证集，训练集用来计算梯度，更新连接权和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。
2. “正则化”(regularization)：在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和，仍令\(E_k\)表示第\(k\)个样例上的误差，\(w_i\)表示连接权和阈值，则误差目标函数为：

\[E=\lambda \frac{1}{m}\sum_{k=1}^mE_k+(1-\lambda)\sum_iw_i^2 \]

其中，\(\lambda \in (0,1)\)用于对经验误差与网络复杂度这两项进行折中，常通过交叉验证法来估计。

扩展

多隐层神经网络难以直接用经典算法（日标准BP算法）进行训练，因为误差在多隐层内逆传播时，往往会“发散”而不能收敛到稳定状态。