栈和队列 - 数据结构
栈(stack):限制仅在表的一端进行插入和删除运算的线性表。其为后进先出(LIFO)的线性表。如下:

顺序栈:栈的顺序存储结构,是运算受限的顺序表。实现如下:
1 #include <iostream> 2 using namespace std; 3 4 #define MaxSize 100 5 #define OK 1 6 #define ERROR 0 7 #define TRUE 1 8 #define FALSE 0 9 typedef int ElemType; 10 typedef int Status; 11 typedef struct { 12 ElemType data[MaxSize]; 13 int top; //指示栈顶的位置 14 } Stack; //顺序栈类型 15 16 //当s->top = -1 表示栈空,s->top = MaxSize -1 表示栈满 17 //初始化顺序栈 18 Status InitStack(Stack &S) { 19 S.top = -1; 20 return OK; 21 } 22 23 //判栈空 24 Status StackEmpty(const Stack &S) { 25 return S.top == -1; 26 } 27 28 //压栈操作 29 Status Push_Stack(Stack &S, ElemType e) { 30 if (MaxSize - 1 == S.top) { 31 return ERROR; 32 } 33 S.data[++S.top] = e; 34 ++S.data[0]; 35 return OK; 36 } 37 38 //出栈 39 Status Pop_Stack(Stack &S, ElemType *e) { 40 if (S.top == -1) { 41 return ERROR; 42 } 43 *e = S.data[S.top--]; 44 return OK; 45 } 46 47 //输出顺序栈中的所有元素 48 void DispStack(const Stack &S) { 49 int i = 0; 50 while (i <= S.top) { 51 printf("%d ", S.data[i]); 52 ++i; 53 } 54 putchar('\n'); 55 } 56 57 int main() { 58 Stack S; 59 int e; 60 InitStack(S); 61 e = StackEmpty(S); 62 printf("%d\n", e); 63 64 for (int i = 0; i < 5; ++i) { 65 Push_Stack(S, i * i); 66 } 67 DispStack(S); 68 69 Pop_Stack(S, &e); 70 printf("%d\n", e); 71 DispStack(S); 72 return 0; 73 }
输出为:
1 5 1 4 9 16 16 5 1 4 9
其中,栈顶的位置随着进栈和退栈操作而变化,用一个top来指示当前栈顶位置。
链栈:栈的链式存储结构。
在一个链栈中,栈底就是链表的最后一个结点,而栈顶总是链表的第一个结点。如下:

1 #include <iostream> 2 using namespace std; 3 4 #define MaxSize 100 5 #define OK 1 6 #define ERROR 0 7 #define TRUE 1 8 #define FALSE 0 9 10 typedef int ElemType; 11 typedef int Status; 12 typedef struct node { //链栈的定义 13 ElemType data; 14 struct node *next; 15 } StackNode, *LinkStack; 16 17 //初始化 18 void InitStack(StackNode *top) { 19 top->next = NULL; 20 } 21 22 //判空 23 Status IsEmpty(StackNode *top) { 24 if (top->next == NULL) return TRUE; 25 return FALSE; 26 } 27 28 //入栈 29 Status Push(StackNode *top, ElemType e) { 30 StackNode *temp; 31 temp = (StackNode *)malloc(sizeof(StackNode)); 32 if (temp == NULL) return FALSE; 33 temp->data = e; 34 temp->next = top->next; 35 top->next = temp; 36 return TRUE; 37 } 38 39 //出栈 40 Status Pop(StackNode *top, ElemType *e) { 41 if (IsEmpty(top)) return FALSE; 42 StackNode *temp = top->next; 43 *e = temp->data; 44 top->next = temp->next; 45 free(temp); 46 return TRUE; 47 } 48 49 //获取栈顶元素 50 void GetTop(StackNode *top, ElemType *e) { 51 *e = top->next->data; 52 } 53 54 int main() { 55 StackNode *s; 56 s = (StackNode *)malloc(sizeof(StackNode)); 57 InitStack(s); 58 for(int i = 0; i < 10; ++i) { 59 Push(s, i); 60 } 61 int e; 62 while(!IsEmpty(s)) { 63 Pop(s, &e); 64 cout << e << ' '; 65 } 66 cout << endl; 67 return 0; 68 }
输出为:
9 8 7 6 5 4 3 2 1 0
队列(Queue):只允许在一端进行插入,而在另一端进行删除的运算受限的线性表。也叫做先进先出(FIFO)的线性表。
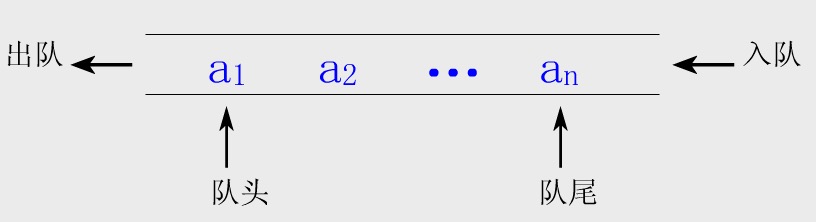
顺序队列:队列的顺序存储结构,是运算受限的顺序表。
1 #include <iostream> 2 using namespace std; 3 4 #define MaxSize 100 5 #define OK 1 6 #define ERROR 0 7 #define TRUE 1 8 #define FALSE 0 9 10 typedef int ElemType; 11 typedef int Status; 12 typedef struct { 13 ElemType data[MaxSize]; 14 int front; 15 int rear; 16 } SeQueue; 17 18 //初始化顺序队列 19 void InitQueue(SeQueue *Q) { 20 Q->front = Q->rear = 0; 21 } 22 23 //判断队列是否为空 24 bool EmptyQueue(SeQueue *Q) { 25 if(Q->front == Q->rear) { 26 cout << "队列空!\n"; 27 return TRUE; 28 } 29 return FALSE; 30 } 31 32 //获取队列头元素 33 Status GetFront(SeQueue *Q, ElemType *e) { 34 if(EmptyQueue(Q)) return ERROR; 35 *e = Q->data[(Q->front+1)%MaxSize]; 36 return OK; 37 } 38 39 //入队 40 Status EnQueue(SeQueue *Q, ElemType e) { 41 if(Q->front == (Q->rear+1)%MaxSize) { 42 cout << "队列满!\n"; 43 return ERROR; 44 } 45 Q->rear = (Q->rear + 1) % MaxSize; 46 Q->data[Q->rear] = e; 47 cout << e << " 入队; rear = " << Q->rear << "; front = " << Q->front << endl; 48 return OK; 49 } 50 51 //出队 52 Status OutQueue(SeQueue *Q, ElemType *e) { 53 if(EmptyQueue(Q)) return ERROR; 54 Q->front = (Q->front + 1) % MaxSize; 55 *e = Q->data[Q->front]; 56 cout << *e << " 出队; rear = " << Q->rear << "; front = " << Q->front << endl; 57 return OK; 58 } 59 60 //打印队列元素 61 Status PrintQueue(SeQueue *Q) { 62 if(EmptyQueue(Q)) return FALSE; 63 for(int i = Q->front + 1; i <= Q->rear; ++i) { 64 cout << Q->data[i] << ' '; 65 } 66 cout << endl; 67 return OK; 68 } 69 70 int main() { 71 SeQueue *Q; 72 Q = (SeQueue *)malloc(sizeof(SeQueue)); 73 cout << "==========初始化顺序队列===========\n"; 74 InitQueue(Q); 75 for(int i = 0; i < 10; ++i) { 76 EnQueue(Q, i); 77 } 78 cout << "==========输出顺序队列元素===========\n"; 79 PrintQueue(Q); 80 81 cout << "==========输出顺序队列头元素===========\n"; 82 ElemType fx; 83 GetFront(Q, &fx); 84 cout << fx << endl; 85 86 cout << "==========顺序队列出栈===========\n"; 87 for(int i = 1; i <= 10; ++i) { 88 OutQueue(Q, &fx); 89 } 90 cout << endl; 91 92 cout << "==========输出顺序队列===========\n"; 93 PrintQueue(Q); 94 return 0; 95 }
输出结果为:
==========初始化顺序队列=========== 0 入队; rear = 1; front = 0 1 入队; rear = 2; front = 0 2 入队; rear = 3; front = 0 3 入队; rear = 4; front = 0 4 入队; rear = 5; front = 0 5 入队; rear = 6; front = 0 6 入队; rear = 7; front = 0 7 入队; rear = 8; front = 0 8 入队; rear = 9; front = 0 9 入队; rear = 10; front = 0 ==========输出顺序队列元素=========== 0 1 2 3 4 5 6 7 8 9 ==========输出顺序队列头元素=========== 0 ==========顺序队列出栈=========== 0 出队; rear = 10; front = 1 1 出队; rear = 10; front = 2 2 出队; rear = 10; front = 3 3 出队; rear = 10; front = 4 4 出队; rear = 10; front = 5 5 出队; rear = 10; front = 6 6 出队; rear = 10; front = 7 7 出队; rear = 10; front = 8 8 出队; rear = 10; front = 9 9 出队; rear = 10; front = 10 ==========输出顺序队列=========== 队列空!
链队列:队列的链式存储结构,是限制仅在表头删除和表尾插入的单链表。

1 #include <iostream> 2 using namespace std; 3 4 #define MaxSize 100 5 #define OK 1 6 #define ERROR 0 7 #define TRUE 1 8 #define FALSE 0 9 10 typedef int ElemType; 11 typedef int Status; 12 typedef struct Lnode { 13 ElemType data; 14 struct Lnode *next; 15 } LinkLisk; 16 17 typedef struct { 18 LinkLisk *front; 19 LinkLisk *rear; 20 } LinkQueue; 21 22 Status InitQueue(LinkQueue *LQ) { 23 LinkLisk *p = (LinkLisk *)malloc(sizeof(LinkLisk)); 24 if(p == NULL) { 25 cout << "初始化失败!\n"; 26 return ERROR; 27 } 28 p->next = NULL; 29 LQ->front = LQ->rear = p; 30 return OK; 31 } 32 33 bool EmptyQueue(LinkQueue *LQ) { 34 if(LQ->front == LQ->rear) { 35 cout << "队列空!\n"; 36 return TRUE; 37 } 38 return FALSE; 39 } 40 41 Status PushQueue(LinkQueue *LQ, ElemType e) { 42 LinkLisk *s = (LinkLisk *)malloc(sizeof(LinkLisk)); 43 if(s == NULL) { 44 cout << "分配空间失败!\n"; 45 return ERROR; 46 } 47 s->data = e; 48 s->next = NULL; 49 LQ->rear->next = s; 50 LQ->rear = s; 51 cout << "入队元素:" << e << endl; 52 return OK; 53 } 54 55 Status GetFront(LinkQueue *LQ, ElemType *e) { 56 if(EmptyQueue(LQ)) return ERROR; 57 *e = LQ->front->next->data; 58 return OK; 59 } 60 61 Status PopQueue(LinkQueue *LQ, ElemType *e) { 62 LinkLisk *p; 63 if(EmptyQueue(LQ)) return ERROR; 64 p = LQ->front->next; 65 *e = p->data; 66 cout << "出队元素:" << *e << endl; 67 LQ->front->next = p->next; 68 if(LQ->front->next == NULL) { 69 LQ->rear = LQ->front; 70 } 71 free(p); 72 return OK; 73 } 74 75 Status PrintQueue(LinkQueue *LQ) { 76 if(EmptyQueue(LQ)) return ERROR; 77 LinkLisk *i = LQ->front->next; 78 while(i) { 79 cout << i->data << ' '; 80 i = i->next; 81 } 82 cout << endl; 83 return OK; 84 } 85 86 int main() { 87 LinkQueue *LQ; 88 LQ = (LinkQueue *)malloc(sizeof(LinkQueue)); 89 cout << "==========初始化链队列==========\n"; 90 InitQueue(LQ); 91 for(int i = 0; i < 10; ++i) { 92 PushQueue(LQ, i); 93 } 94 cout << "==========输出链队列元素==========\n"; 95 PrintQueue(LQ); 96 97 cout << "==========获取队列首元素==========\n"; 98 ElemType fe; 99 GetFront(LQ, &fe); 100 cout << fe << endl; 101 102 cout << "==========出链队列==========\n"; 103 for(int i = 0; i < 10; ++i) { 104 PopQueue(LQ, &fe); 105 } 106 cout << "==========输出链队列元素==========\n"; 107 PrintQueue(LQ); 108 return 0; 109 }
输出为:
==========初始化链队列========== 入队元素:0 入队元素:1 入队元素:2 入队元素:3 入队元素:4 入队元素:5 入队元素:6 入队元素:7 入队元素:8 入队元素:9 ==========输出链队列元素========== 0 1 2 3 4 5 6 7 8 9 ==========获取队列首元素========== 0 ==========出链队列========== 出队元素:0 出队元素:1 出队元素:2 出队元素:3 出队元素:4 出队元素:5 出队元素:6 出队元素:7 出队元素:8 出队元素:9 ==========输出链队列元素========== 队列空!





