哈夫曼树模板+例题

核心代码

while (q.size() > 1) {
        x = q.top();
        q.pop();
        x += q.top();
        q.pop();
        q.push(x);
        sum += x;
    }

Ploblem A Huffman Coding on Segment

Alice wants to send an important message to Bob. Message $a=(a_1,...,a_n)$ is a sequence of positive integers (characters).

To compress the message Alice wants to use binary Huffman coding. We recall that binary Huffman code, or binary prefix code is a function $f$ , that maps each letter that appears in the string to some binary string (that is, string consisting of characters $'0'$ and $'1'$ only) such that for each pair of different characters ai $a_{i}$ and $a_{j}$ string $ f(a_{i})$ is not a prefix of $f(a_{j})$ (and vice versa). The result of the encoding of the message $a_{1},a_{2},...,a_{n}$ is the concatenation of the encoding of each character, that is the string $f(a_1)f(a_2)...f(a_n) $ . Huffman codes are very useful, as the compressed message can be easily and uniquely decompressed, if the function f f f is given. Code is usually chosen in order to minimize the total length of the compressed message, i.e. the length of the string $f(a_{1})f(a_{2})...\ f(a_{n})$.

Because of security issues Alice doesn't want to send the whole message. Instead, she picks some substrings of the message and wants to send them separately. For each of the given substrings $a_{li}...\ a_{ri}$ she wants to know the minimum possible length of the Huffman coding. Help her solve this problem.

Input

The first line of the input contains the single integer $n$ $(1 \leq n \leq 100 000)$ — the length of the initial message. The second line contains n integers $a_1, a_2, ..., a_n (1 \leq a_i \leq 100 000)$ — characters of the message.

Next line contains the single integer $q (1 \leq q \leq 100 000)$ — the number of queries.

Then follow $q$ lines with queries descriptions. The i-th of these lines contains two integers $l_i$ and $r_i$ $(1 \leq l_i \leq r_i \leq n)$ — the position of the left and right ends of the i-th substring respectively. Positions are numbered from $1$. Substrings may overlap in any way. The same substring may appear in the input more than once.

Output

Print $q$ lines. Each line should contain a single integer — the minimum possible length of the Huffman encoding of the substring $a_{l_i}... .a_{r_i}$.

Sample Input

$7$

$1$ $2$ $1$ $3$ $1$ $2$ $1$

$5$

$1$ $7$

$1$ $3$

$3$ $5$

$2$ $4$

$4$ $4$

Sample Output

$10$

$3$

$5$

$0$

Hint

In the first query, one of the optimal ways to encode the substring is to map $1$ to "$0$", $2$ to "$10$" and $3$ to "$11$".

Note that it is correct to map the letter to the empty substring (as in the fifth query from the sample).

Description

给定一段序列$a$，有$q$个询问，每次询问给定$l$和$r$，求$a_l..a_r$的$Huffman$编码长度。

Solution

以每个字符出现的次数为点权，边权为$1$建一棵$Huffman$树，$WPL$就是这段字符串的$Huffman$编码长度，所以可以用莫队维护每个字符出现的次数，然后建$Huffman$树，然后发现这样会$TLE$，于是可以把出现次数小于等于$sqrt(n)$次的处理掉，剩下大于$sqrt(n)$的再建$Huffman$树。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 315;
struct Node {
    int l, r, id;
} tr[N];
priority_queue<int, vector<int>, greater<int> > q;
vector<int> v;
int n, m, l, r, a[N], f[N], f1[N], aa[N], ans[N];
inline int read() {
    char ch; bool f = false; int res = 0;
    while (((ch = getchar()) < '0' || ch > '9') && ch != '-');
    if (ch == '-') f = true; else res = ch - '0';
    while ((ch = getchar()) >= '0' && ch <= '9') res = (res << 3) + (res << 1) + ch - '0';
    return f? ~res + 1 : res;
}
inline bool cmp(Node a, Node b) {
    return a.l / M == b.l / M ? a.r < b.r : a.l < b.l;
}
inline void Build (int x, int y) {
    --f[f1[x]], f1[x] += y, ++f[f1[x]];
}
inline int solve() {
    for (int i = 0; i < v.size(); i++)
        if (f1[v[i]] > M)
            q.push(f1[v[i]]);
    for (int i = 1; i <= M; i++)
        a[i] = f[i];
    int ans = 0, j = 0;
    for (int i = 1; i <= M; i++)
        if (a[i]) {
            if (j) {
                if (i + j > M) q.push(i + j); else ++a[i + j];
                --a[i], ans += i + j, j = 0;
            }
            if (a[i] & 1) --a[i], j = i;
            ans += a[i] * i;
            if ((i << 1) > M)
                for (int p = a[i] >> 1; p; --p) q.push(i << 1);
            else a[i << 1] += a[i] >> 1;
        }
    if (j)
        q.push(j);
    while (!q.empty()) {
        int x = q.top(); 
        q.pop();
        if (q.empty()) break;
        x = x + q.top();
        q.pop();
        ans += x;
        q.push(x);
    }
    return ans;
}
int main() {
    n = read();
    for (int i = 1; i <= n; i++)
        ++f1[aa[i] = read()];
    for (int i = 1; i <= N - 10; i++)
        if (f1[i] > M) v.push_back(i);
    for (int i = 1; i <= N - 10; i++)
        f1[i] = 0;
    m = read(), l = 1, r = 0;
    for (int i = 1; i <= m; i++)
        tr[i].l = read(), tr[i].r = read(), tr[i].id = i;
    std::sort(tr + 1, tr + m + 1, cmp);
    for (int i = 1; i <= m; i++) {
        while (r < tr[i].r) Build(aa[++r], 1);
        while (l > tr[i].l) Build(aa[--l], 1);
        while (r > tr[i].r) Build(aa[r--], -1);
        while (l < tr[i].l) Build(aa[l++], -1);
        ans[tr[i].id] = solve();
    }
    for (int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);
    return 0;
}

Problem B Fence Repair (POJ $3253$)

Farmer John wants to repair a small length of the fence around the pasture. He measures the fence and finds that he needs N ($1 \leq N \leq 20,000$) planks of wood, each having some integer length $L_i$ ($1 \leq L_i \leq 50,000$) units. He then purchases a single long board just long enough to saw into the $N$ planks (i.e., whose length is the sum of the lengths Li). FJ is ignoring the "kerf", the extra length lost to sawdust when a sawcut is made; you should ignore it, too.

FJ sadly realizes that he doesn't own a saw with which to cut the wood, so he mosies over to Farmer Don's Farm with this long board and politely asks if he may borrow a saw.

Farmer Don, a closet capitalist, doesn't lend FJ a saw but instead offers to charge Farmer John for each of the N-1 cuts in the plank. The charge to cut a piece of wood is exactly equal to its length. Cutting a plank of length 21 costs 21 cents.

Farmer Don then lets Farmer John decide the order and locations to cut the plank. Help Farmer John determine the minimum amount of money he can spend to create the N planks. FJ knows that he can cut the board in various different orders which will result in different charges since the resulting intermediate planks are of different lengths.

Input

Line $1$: One integer $N$, the number of planks
Lines $2$..$N+1$: Each line contains a single integer describing the length of a needed plank

Output

Line $1$: One integer: the minimum amount of money he must spend to make $N-1$ cuts

Sample Input

$3$

$8$

$5$

$8$

Sample Output

$34$

Hint

He wants to cut a board of length $21$ into pieces of lengths $8$, $5$, and $8$.The original board measures $8+5+8=21$. The first cut will cost $21$, and should be used to cut the board into pieces measuring $13$ and $8$.The second cut will cost $13$, and should be used to cut the $13$ into $8$ and $5$. This would cost $21+13=34$. If the $21$ was cut into $16$ and $5$ instead, the second cut would cost 16 for a total of $37$ (which is more than $34$).

Description

FJ要修补围栏，他需要$n$块长度为$L_i$的木头。开始时，有一块无限长的木板需要锯成$n$块长度为$L_i$的木板，收费的标准为每次锯出的长度。求总价值最小。

Solution

这题显然是$Huffman$树的模板题。先在$N$ $planks$中每次找出两块长度最短的木板，把他们合并，并放进集合$A$中，然后再集合$A$中找出两块长度最短的木板，合并继续放进集合中，一直重复这个过程，直到集合中只剩下一个元素。

#include<bits/stdc++.h>
using namespace std;
int n, x;
long long sum;
priority_queue<int,vector<int>,greater<int> >q;
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &x);
        q.push(x);
    }
    if (q.size() == 1) {
        sum += q.top();
        q.pop();
    }
    while (q.size() > 1) {
        x = q.top();
        q.pop();
        x += q.top();
        q.pop();
        q.push(x);
        sum += x;
    }
    printf("%lld\n", sum);
    return 0;
}

Ploblem C [NOI2015]荷马史诗

追逐影子的人，自己就是影子 ——荷马

$Allison$ 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，$Allison$ 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有$n$种不同的单词，从$1$到$n$进行编号。其中第i种单词出现的总次数为$w_i$。$Allison$ 想要用$k$进制串$s_i$来替换第i种单词，使得其满足如下要求：

对于任意的 $1 \leq i, j \leq n$ ， $i ≠ j$ ，都有：$s_i$不是$s_j$的前缀。

现在 $Allison$ 想要知道，如何选择$s_i$，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，$Allison$ 还想知道最长的si的最短长度是多少？

一个字符串被称为$k$进制字符串，当且仅当它的每个字符是 $0$ 到 $k − 1$ 之间（包括 0 和 k − 1 ）的整数。

字符串 $str1$ 被称为字符串 $str2$ 的前缀，当且仅当：存在 $1 \leq t \leq m$ ，使得$str1 = str2[1..t]$。其中，$m$是字符串$str2$的长度，$str2[1..t]$ 表示$str2$的前$t$个字符组成的字符串。

Input

输入的第 $1$ 行包含 $2$ 个正整数 $n$, $k$ ，中间用单个空格隔开，表示共有$n$种单词，需要使用$k$进制字符串进行替换。

接下来$n$行，第 $i + 1$ 行包含 $1$ 个非负整数$w_i$ ，表示第 $i$ 种单词的出现次数。

Output

输出包括 $2$ 行。

第 $1$ 行输出 $1$ 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 $2$ 行输出 $1$ 个整数，为保证最短总长度的情况下，最长字符串 $s_i$ 的最短长度。

Sample Input 1

$4$ $2$

$1$

$2$

Sample Output 1

$12$

$2$

Sample Input 2

$6$ $3$

$1$

$3$

$9$

Sample Output 2

$36$

$3$

Code

// luogu-judger-enable-o2
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
long long ans, sum, a[N];
int n, k, n1, x;
inline long long read() {
    char ch; bool f = false; long long res = 0;
    while (((ch = getchar()) < '0' || ch > '9') && ch != '-');
    if (ch == '-') f = true; else res = ch - '0';
    while ((ch = getchar()) >= '0' && ch <= '9') res = (res << 3) + (res << 1) + ch - '0';
    return f? ~res + 1 : res;
}
struct Node {
    long long x;
    int y;
    inline bool operator<(const Node &a) const {
        return x > a.x || (x == a.x && y > a.y);
    }
};
priority_queue<Node> q;
int main() {
    n = read(), k = read(), n1 = (n - 1 + k - 2) / (k - 1) * (k - 1) + 1;
    for (int i = 1; i <= n1; ++i)
        if (i <= n) {
            a[i] = read();
            q.push((Node) {a[i], 1});
        }
        else 
            q.push((Node) {0, 1});
    for (int i = n1; i > 1; i -= (k - 1)) {
        sum = 0, x = 0;
        for (int j = 1; j <= k; ++j) {
            sum += (q.top()).x, x = std::max(x, (q.top()).y);
            q.pop();
        }
        q.push((Node){sum, x + 1});ans += sum;
    }
    printf("%lld\n%d\n", ans, q.top().y - 1);
    return 0;
}

Ploblem D UVA 12676 Inverting Huffman

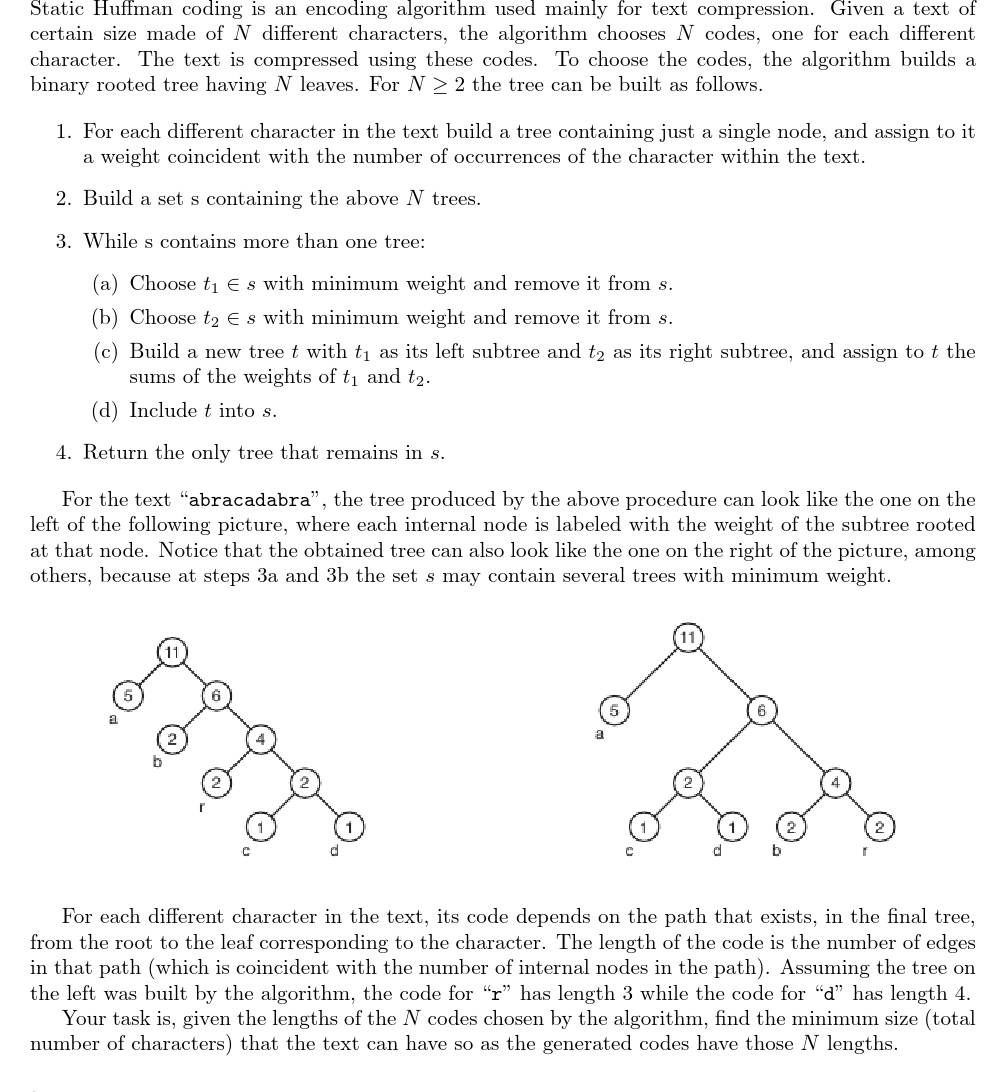
avatar

avartar

Description

一串文本中包含 $N$ 个不同字母，经过哈夫曼编码后，得到这 $N$ 个字母的相应编码长度，求文本的最短可能长度

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
struct Node {
    int id;
    long long v;
    friend bool operator < (Node a, Node b) {
        if (a.id == b.id) 
            return a.v < b.v;
        else
            return a.id < b.id;	
    }
} a[N];
int n, maxx;
long long ans, f[N];
Node x, y;
priority_queue<Node> q;
inline void init (int n) {
    while (!q.empty())
        q.pop();
    for (int i = 1; i <= n; i++)
        a[i].v = -1;
    memset(f, 0, sizeof(f));
    maxx = -1, ans = 0;
}
int main() {
    while (~scanf("%d", &n)) {
        init(n);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i].id);
            maxx = std::max(maxx, a[i].id);
            q.push(a[i]);
        }
        f[maxx] = 1;
        while (!q.empty()) {
            x = q.top();
            q.pop();
            if (q.empty()) {
                ans = x.v;
                break;
            }
            y = q.top();
            q.pop();
            if (x.id == maxx && y.id == maxx)
                x.v = y.v = 1;
            else {
                if (x.v == -1)
                    x.v = f[x.id + 1];
                if (y.v == -1)
                    y.v = f[y.id + 1];
            }
            x.id = x.id - 1, x.v = x.v + y.v;
            f[x.id] = std::max(f[x.id], x.v);
            q.push(x);
        }
        printf("%lld\n", ans);
    }
    return 0;
}

posted @ 2019-06-22 20:22 Trimsteanima 阅读(1211) 评论(0) 编辑收藏举报

刷新页面返回顶部

Trimsteanima

哈夫曼树模板+例题

核心代码

Ploblem A Huffman Coding on Segment

Input

Output

Sample Input

Sample Output

Hint

Description

Solution

Problem B Fence Repair (POJ \(3253\))

Input

Output

Sample Input

Sample Output

Hint

Description

Solution

Ploblem C [NOI2015]荷马史诗

Input

Output

Sample Input 1

Sample Output 1

Sample Input 2

Sample Output 2

Code

Ploblem D UVA 12676 Inverting Huffman

Description

公告

Trimsteanima

哈夫曼树 模板+例题

核心代码

Ploblem A Huffman Coding on Segment

Input

Output

Sample Input

Sample Output

Hint

Description

Solution

Problem B Fence Repair (POJ \(3253\))

Input

Output

Sample Input

Sample Output

Hint

Description

Solution

Ploblem C [NOI2015]荷马史诗

Input

Output

Sample Input 1

Sample Output 1

Sample Input 2

Sample Output 2

Code

Ploblem D UVA 12676 Inverting Huffman

Description

公告

哈夫曼树模板+例题