BB方法与最速下降法的对比程序 

 1 import numpy as np
 2 import matplotlib.pyplot as plt
 3 plt.rcParams['font.sans-serif']=['Microsoft YaHei']
 4 
 5 def f(y): #目标函数
 6     f_x=y[0]**2+10*y[1]**2
 7     return f_x
 8 
 9 def df(y): #函数梯度
10     df_y=np.array([2*y[0],20*y[1]])
11     return df_y
12 
13 def DG_method(start,eps): #最速下降法
14 
15     #分别记录迭代点、迭代点的函数值、迭代点的梯度、梯度模长
16     X=np.zeros((1000,2))
17     F=np.zeros((1000,1))
18     dF=np.zeros((1000,2))
19     dF_norm=np.zeros((1000,1))
20     X[0,:]=start #初始迭代点
21     F[0]=f(X[0])
22     dF[0,:]=df(X[0])
23     dF_norm[0]=np.linalg.norm(dF[0,:])
24     k=0
25  
26     while (dF_norm[k]>=eps)  :
27         alpha=np.dot(dF[k,:],dF[k,:])/np.dot(dF[k,:],np.dot([[2,0],[0,20]],dF[k,:])) #计算步长，此处直接使用的最速下降的步长
28         X[k+1,:]=X[k,:]-alpha*dF[k,:]
29         F[k+1]=f(X[k+1,:])
30         dF[k+1,:]=df(X[k+1,:])
31         dF_norm[k+1]=np.linalg.norm(dF[k+1,:])
32 
33         k=k+1
34         
35     return k,X[k,:],F[k,:],X,F,dF_norm
36 
37 def BB_method(start,eps,alpha=1,alpham=0.05,alphaM=2,M=10,c1=0.2,beta=0.3): #BB方法
38 
39     #分别记录迭代点、迭代点的函数值、迭代点的梯度、梯度模长
40     X=np.zeros((1000,2))
41     F=np.zeros((1000,1))
42     dF=np.zeros((1000,2))
43     dF_norm=np.zeros((1000,1))
44     X[0,:]=start #初始迭代点
45     F[0]=f(X[0])
46     dF[0,:]=df(X[0])
47     dF_norm[0]=np.linalg.norm(dF[0,:])
48     k=0
49  
50     while dF_norm[k]>=eps :
51         while f(X[k,:]-alpha*dF[k,:])>= max(F[max(0,k-M):k+1])-c1*alpha*dF_norm[k]**2 : #对步长进行修正
52             alpha=beta*alpha
53         X[k+1,:]=X[k,:]-alpha*dF[k,:]
54         F[k+1]=f(X[k+1,:])
55         dF[k+1,:]=df(X[k+1,:])
56         dF_norm[k+1]=np.linalg.norm(dF[k+1,:])
57        
58         s=X[k+1,:]-X[k,:]        
59         y=dF[k+1,:]-dF[k,:]
60         #alpha=np.dot(s,s)/np.dot(s,y)
61         alpha=min([max([np.dot(s,s)/np.dot(s,y),alpham]),alphaM]) #对步长进行截断
62         k=k+1
63         
64     return k,X[k,:],F[k,:],X,F,dF_norm
65 
66 K,x_min,f_min,X,F,dF_norm=BB_method([-10,-1],1e-6)
67 print("利用BB方法: 迭代次数 = ",K ,",最优值点 = ",x_min,",最小值 = ",f_min)
68 
69 K1,x_min1,f_min1,X1,F1,dF_norm1=DG_method([10,1],1e-6)
70 print("利用最速下降法：迭代次数 = ",K1 ,",最优值点 = ",x_min1,",最小值 = ",f_min1)
71 
72 
73 def Go_plot(K1,X1,F1,dF_norm1,K2,X2,F2,dF_norm2): #对迭代点位置、函数值下降、梯度范数下降曲线画图，将两个方法的结果对比
74     plt.figure()
75     plt.plot(X1[0:K1+1,0],X1[0:K1+1,1])
76     plt.plot(X2[0:K2+1,0],X2[0:K2+1,1])
77     plt.legend(['BB方法','最速下降法'])
78 
79     plt.figure()
80     plt.plot(range(K1+1),np.log(dF_norm1[0:K1+1]))
81     plt.plot(range(K2+1),np.log(dF_norm2[0:K2+1]))
82     plt.legend(['BB方法','最速下降法'])
83     plt.xlabel('迭代次数')
84     plt.ylabel('梯度范数模长的对数')
85     
86     plt.figure()
87     plt.plot(range(K1+1),np.log(F1[0:K1+1]))
88     plt.plot(range(K2+1),np.log(F2[0:K2+1]))
89     plt.legend(['BB方法','最速下降法'])
90     plt.xlabel('迭代次数')
91     plt.ylabel('目标函数值的对数')
92 
93     plt.show()
94 
95 Go_plot(K,X,F,dF_norm,K1,X1,F1,dF_norm1)
96 
97 
98

利用BB方法: 迭代次数 = 21 ,最优值点 = [-2.46698420e-08 2.06260876e-12] ,最小值 = [6.08601148e-16]
利用最速下降法：迭代次数 = 86 ,最优值点 = [3.19952043e-07 3.19952043e-08] ,最小值 = [1.12606241e-13]

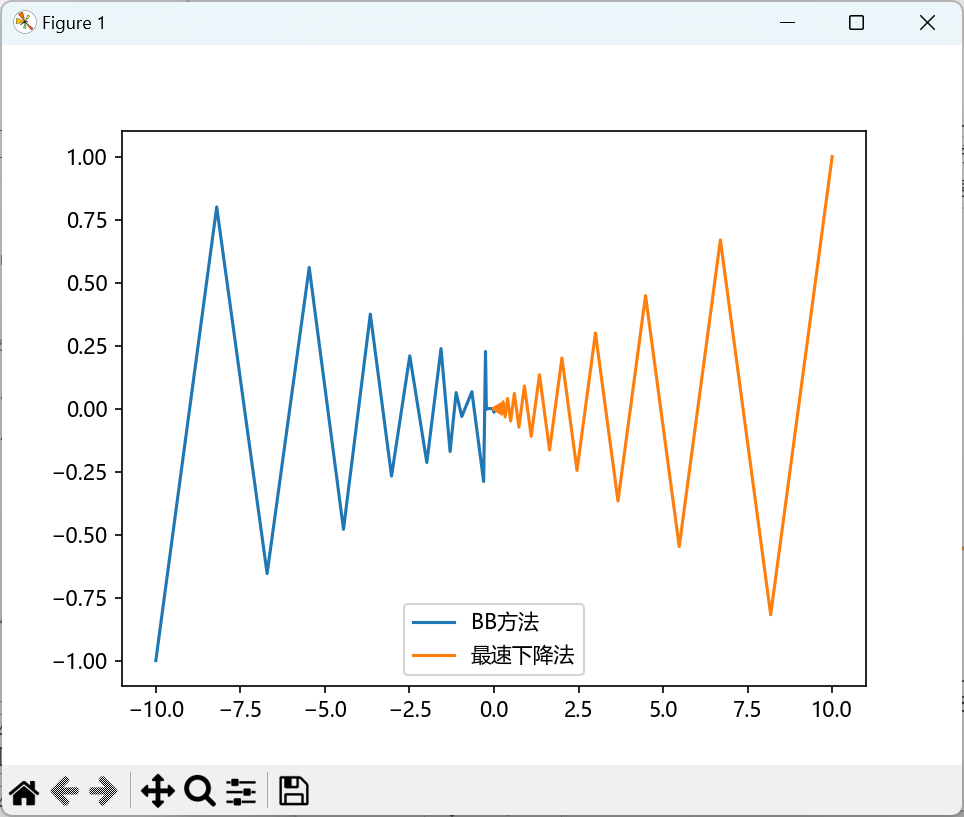
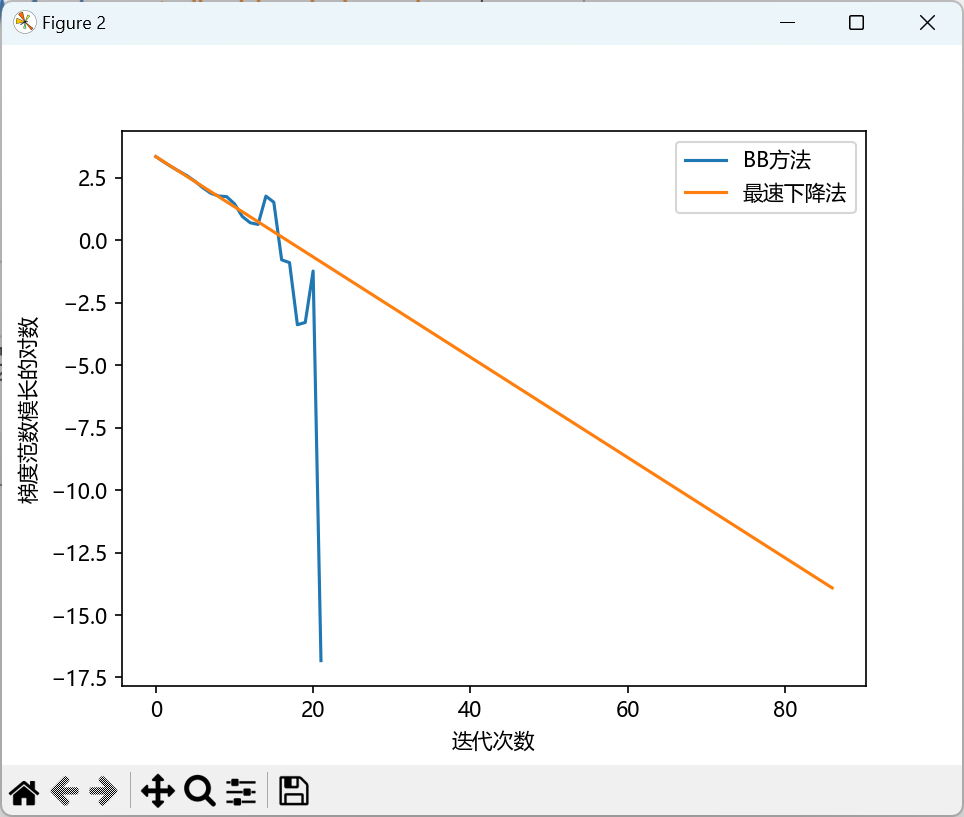
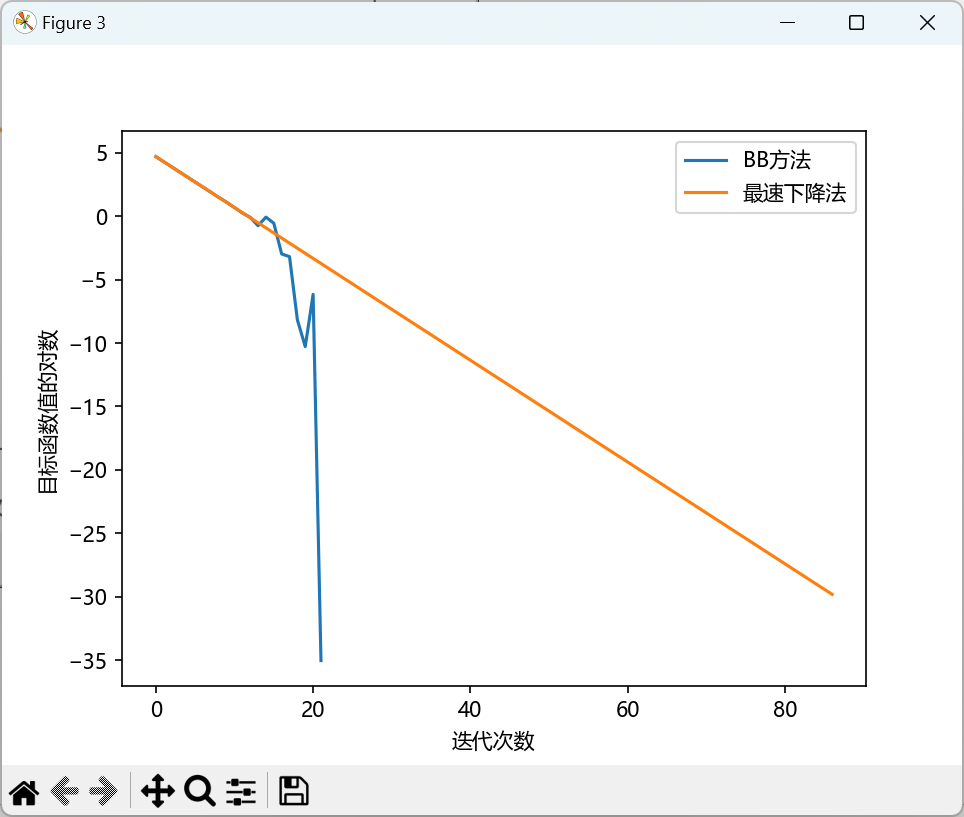
下面的三张对比图：

 

  

 

 

posted @ 2024-02-28 19:39  来者可追2019  阅读(25)  评论(0)  编辑  收藏  举报