集训Day 4

 

比赛开始，先看了一眼A题，great！这个数据写一个DFS就可以过100%于是就开始写DFS但是一直爆，数组也没越界，也没开太大，我就十分奇怪，于是就这样调了大约十来分钟发现是因为遍历器的问题（我已经因为遍历器炸了2次了，再也不用遍历器了Q w Q）将遍历器换成正常的for循环就过了（get100pt）。然后看了第二题，em……没有思路，为了保分只能硬着头皮写了两个打表的程序，但是，第二个打表的程序没写好，导致直接浪费了30分钟。（哭）最后一会我就写了一个DFS充数。（get40pt）。总分140

 

TIPS:
1. 对自己高要求：禁止考试有任意一道题目爆零！都要写暴力！
2. 检查文件名、freopen、多组数据清空、输出换行等sb错误
3. 搜索回溯是对称的
4. 搜索的两种模式：一种是到该点时，该点信息已经处理完毕；一种是到该点时先处理该点信息再搜索。无论 DFS 还是 BFS 均符合，如果思路杂交会非常混乱。
5. 三行 01 背包代码要吃透并且熟练。
6. 得到所有数的约数之和的另类写法：考虑将 i 贡献到 i 的倍数上，相较于直接暴力的 O(n 根号 n)，这个做法是 O(n log n) 的
7. 初赛强度取决于省份，现在初赛要求较高，一定认真对待初赛！！！！
8. 分辨率的 4096*2160 指的是像素，一个像素可能是 32 位 24 位等
9. STL <algorithm> 库中有 nth_element 函数，可以在 O(n) 时间内求出一个序列的第 k 大的数字
10. 存储二叉树一般是左儿子是自己下标乘二，右儿子是自己下标*2+1
11. A 班 5 风纪委员，B 班 4，C 班 3，要出六名委员，问方案数（只关心每个班出的人数），考虑出的人数长什么样（6 0 0, 5 1 0, 4 2 0, 3 3 0）等
12. 排序的稳定性：比较关键字时，若关键字相同，不能改变他们的相对顺序就叫稳定
13. 生成 [a, b) 的数字：
14. memset(a, -1/255/0x3F/0, sizeof(a)) 分别什么意思？
15. 对于杨辉三角和组合数的敏感度？

 

 

 

B题题解：

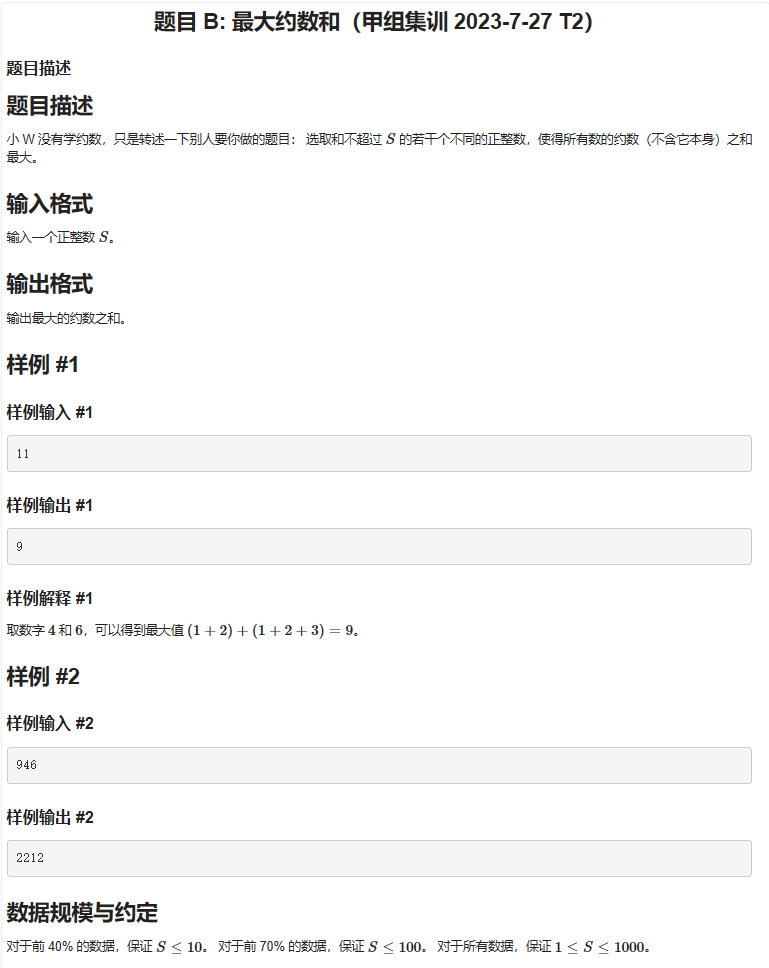
这道题是一道01背包（灵异背包），板子部分不再赘述，按照题意将题目转化为 背包容量为S现要求塞入若干个数，每个数的所占空间为其本身大小，装完后要求背包中所有数的最大公约数最大，问最大多少？简单了？

 A题程序：

#include<bits/stdc++.h>
using namespace std;
//const int N=1e3;
int n,m,vis[11451],ans=0;
vector<int> mp[19198];
void dfs(int k,int step)
{
    if(step==n) ans++;
    else
    {
        for(int i=0;i<mp[k].size();i++)
        {
            if(vis[mp[k][i]]==0)
            {
                vis[mp[k][i]]=1;
                dfs(mp[k][i],step+1);
                vis[mp[k][i]]=0;
            }
        }
    }
}
int main()
{
    freopen( "hami.in", "r", stdin );
     freopen( "hami.out", "w", stdout );
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--)
    {
        ans=0;
        cin>>n>>m;
        for(int i=1;i<=n;i++) mp[i].clear();
        for(int i=1;i<=m;i++)
        {
            int u,v;
            cin>>u>>v;
            mp[u].push_back(v);
            mp[v].push_back(u);
        }
        for(int i=1;i<=n;i++) vis[i]=0;
        vis[1]=1;
        dfs(1,1);
        printf("%d\n",ans);
    }
    return 0;
}

 

B题程序：

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int S,sum[N],f[N];
int main()
{
    ios::sync_with_stdio(false);
    cin>>S;
    for(int i=1;i<=S;i++) for(int j=2;i*j<=S;j++) sum[i*j]+=i;
    for(int i=1;i<=S;i++) for(int j=S;j>=1;j--) f[j]=max(f[j],f[j-i]+sum[i]);
    int maxn=-100;
    for(int i=1;i<=S;i++) maxn=max(maxn,f[i]);
    cout<<maxn;
    return 0;
}