1961: 硬币组合

 

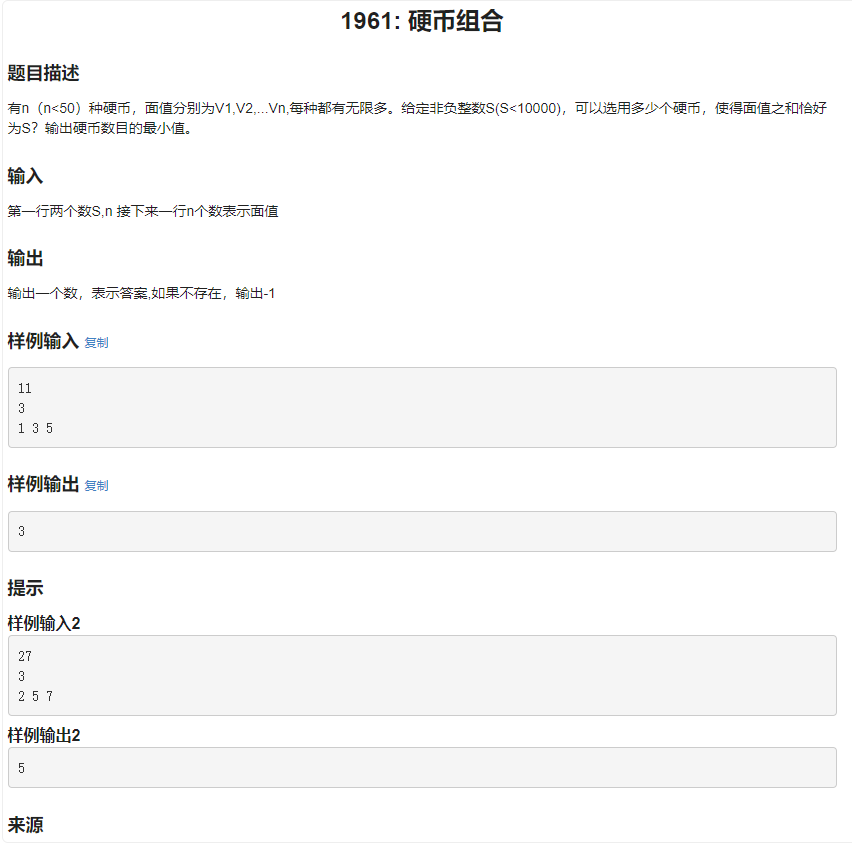
 这道题目是一道经典的DP：

讲一下思路：

f[i]:指i元可以用最少多少张钞票凑齐，凑不齐的话值为-1

先将f数组初始化为无穷大（因为后面有min操作所以不能用-1）

输入的同时将f[a[i]]设为1（举个例子：有一张五元的钞票要凑5元，可以只用一张钞票完成任务）

将f[0]设为0（又一个初始化）

再来一个n²的双重i j 循环，i从1到s 表示要凑齐i元，j从1到n表示遍历一遍所有的钞票。

先判断i-a[j]是否超界。（后面会用到）

我们可以从要凑成的钱数里减去5元再在所用的钞票数里加上1，用算式表达：f[i-a[j]]+1,还要再f[i]和它之间去小值（因为f[i]可能之前已经有值了）

最后判断f[s]是否为最大值（0x3f3f3f3f）如果是的话，说明凑不出来，输出-1，否则输出它的值。

程序结束。

程序：

#include<bits/stdc++.h>
using namespace std;
int s,n,f[100100]={0},a[60]={0};
int main()
{
#ifdef LOCAL
    freopen( "1.in", "r", stdin );
    freopen( "1.out", "w", stdout );
#endif
    scanf("%d%d",&s,&n);
    memset(f,0x3f3f3f3f,sizeof f);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        f[a[i]]=1;
    }
    f[0]=0;
    for(int i=1;i<=s;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i-a[j]>=0)
            {
                f[i]=min(f[i],f[i-a[j]]+1);
            }
        }
    }
    if(f[s]==0x3f3f3f3f) cout<<"-1";
    else cout<<f[s];
    return 0;
}