10 种聚类算法的完整 Python 操作示例
一.聚类
聚类分析,即聚类,是一项无监督的机器学习任务。它包括自动发现数据中的自然分组。与监督学习(类似预测建模)不同,聚类算法只解释输入数据,并在特征空间中找到自然组或群集。
群集通常是特征空间中的密度区域,其中来自域的示例(观测或数据行)比其他群集更接近群集。群集可以具有作为样本或点特征空间的中心(质心),并且可以具有边界或范围。
聚类可以作为数据分析活动提供帮助,以便了解更多关于问题域的信息,即所谓的模式发现或知识发现。例如:
- 该进化树可以被认为是人工聚类分析的结果;
- 将正常数据与异常值或异常分开可能会被认为是聚类问题;
- 根据自然行为将集群分开是一个集群问题,称为市场细分。
聚类还可用作特征工程的类型,其中现有的和新的示例可被映射并标记为属于数据中所标识的群集之一。虽然确实存在许多特定于群集的定量措施,但是对所识别的群集的评估是主观的,并且可能需要领域专家。通常,聚类算法在人工合成数据集上与预先定义的群集进行学术比较,预计算法会发现这些群集。
二.聚类算法
有许多类型的聚类算法。许多算法在特征空间中的示例之间使用相似度或距离度量,以发现密集的观测区域。因此,在使用聚类算法之前,扩展数据通常是良好的实践。
一些聚类算法要求指定或猜测数据中要发现的群集的数量,而另一些算法要求指定观测之间的最小距离,其中示例可以被视为“关闭”或“连接”。因此,聚类分析是一个迭代过程,在该过程中,对所识别的群集的主观评估被反馈回算法配置的改变中,直到达到期望的或适当的结果。scikit-learn 库提供了一套不同的聚类算法供选择。下面列出了10种比较流行的算法:
-
亲和力传播
-
聚合聚类
-
BIRCH
-
DBSCAN
-
K-均值
-
Mini-Batch K-均值
-
Mean Shift
-
OPTICS
-
光谱聚类
- 高斯混合
每个算法都提供了一种不同的方法来应对数据中发现自然组的挑战。没有最好的聚类算法,也没有简单的方法来找到最好的算法为您的数据没有使用控制实验。
三.聚类算法示例
1.库安装
使用 pip 安装 scikit-learn 存储库,如下所示:
sudo pip install scikit-learn
确认已经安装了库:
# 检查 scikit-learn 版本 import sklearn print(sklearn.__version__)
运行该示例时,您应该看到以下版本号或更高版本。
0.22.1
2.聚类数据集
使用 make _ classification ()函数创建一个测试二分类数据集。数据集将有1000个示例,每个类有两个输入要素和一个群集。
# 综合分类数据集 from numpy import where from sklearn.datasets import make_classification from matplotlib import pyplot # 定义数据集 X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 为每个类的样本创建散点图 for class_value in range(2): # 获取此类的示例的行索引 row_ix = where(y == class_value) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
用散点图绘制数据,并通过指定的群集对图中的点进行颜色绘制。
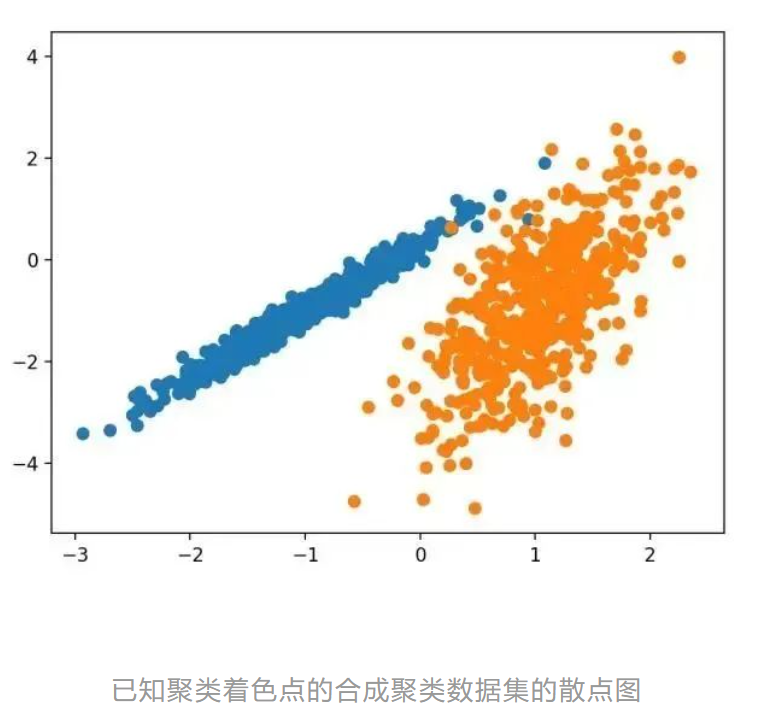
希望一个自动的聚类算法可以检测这些分组。
3.亲和力传播聚类算法
亲和力传播包括找到一组最能概括数据的范例。
我们设计了一种名为“亲和传播”的方法,它作为两对数据点之间相似度的输入度量。在数据点之间交换实值消息,直到一组高质量的范例和相应的群集逐渐出现
—源自:《通过在数据点之间传递消息》2007。
它是通过 AffinityPropagation 类实现的,要调整的主要配置是将“ 阻尼 ”设置为0.5到1,甚至可能是“首选项”。
下面列出了完整的示例。
# 亲和力传播聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AffinityPropagation from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AffinityPropagation(damping=0.9) # 匹配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,无法取得良好的结果。
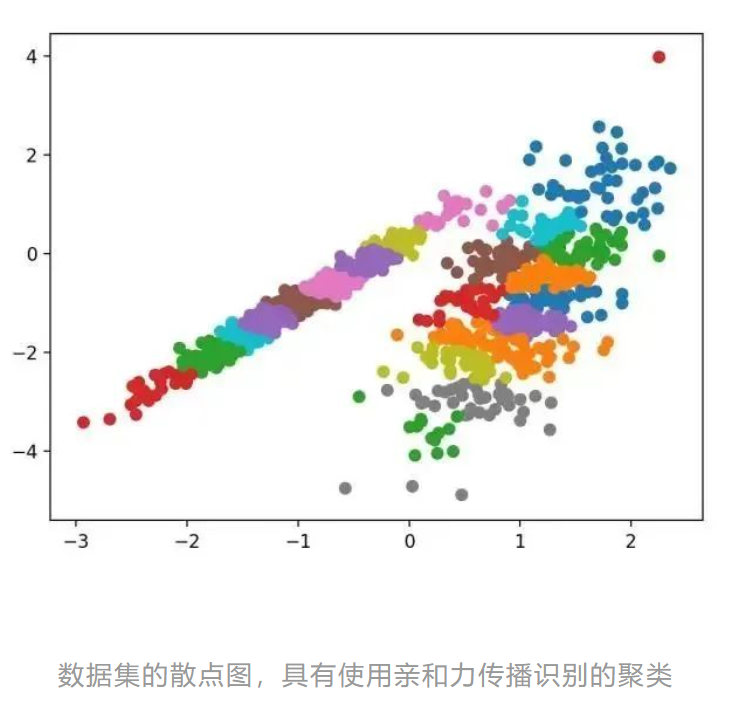
4.聚合聚类
聚合聚类涉及合并示例,直到达到所需的群集数量为止。它是层次聚类方法的更广泛类的一部分,通过 AgglomerationClustering 类实现的,主要配置是“ n _ clusters ”集,这是对数据中的群集数量的估计,例如2。下面列出了完整的示例。
# 聚合聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AgglomerativeClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AgglomerativeClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个合理的分组。
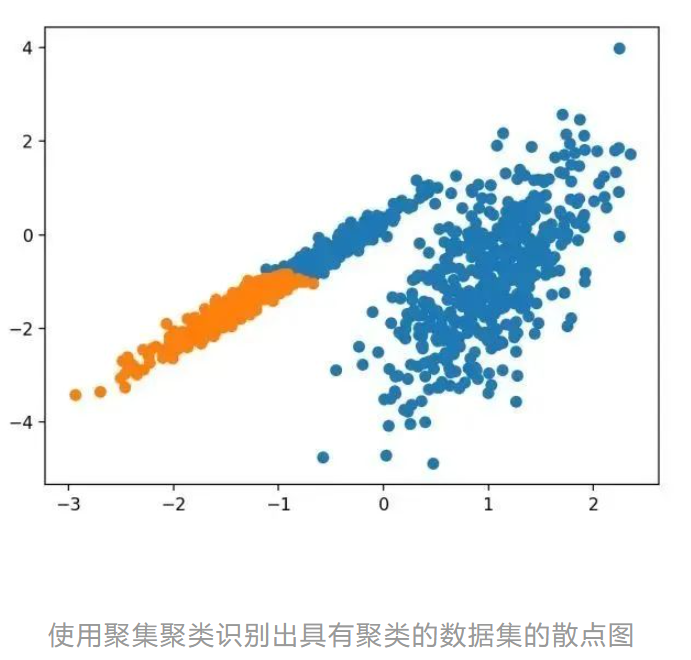
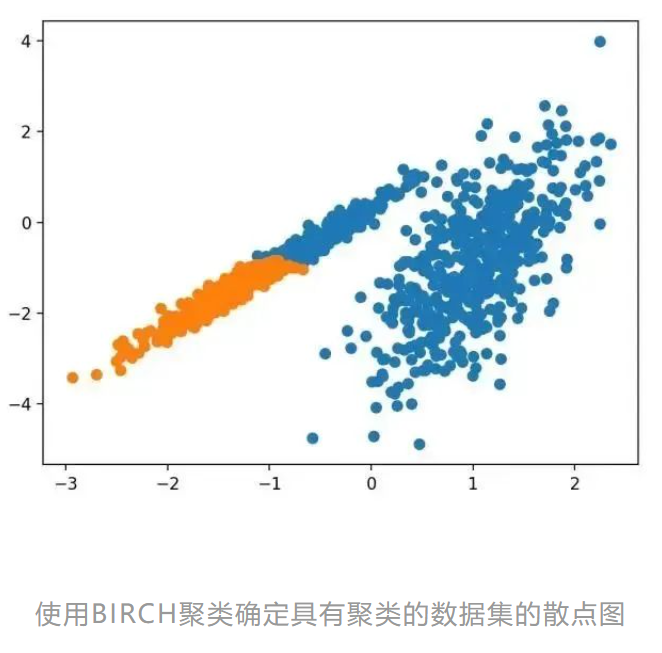
5.BIRCH
BIRCH 聚类( BIRCH 是平衡迭代减少的缩写,聚类使用层次结构)包括构造一个树状结构,从中提取聚类质心。
它是通过 Birch 类实现的,主要配置是“ threshold ”和“ n _ clusters ”超参数,后者提供了群集数量的估计。下面列出了完整的示例。
# birch聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import Birch from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = Birch(threshold=0.01, n_clusters=2) # 适配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个很好的分组。
6.DBSCAN
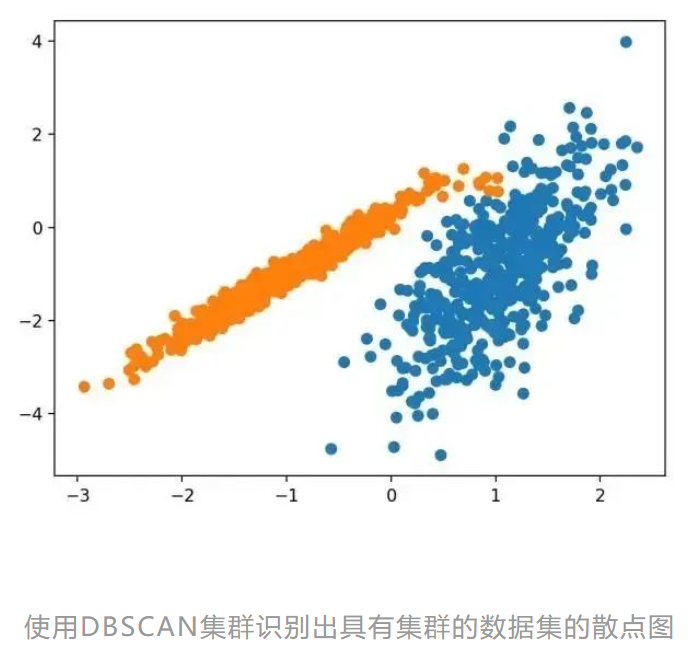
DBSCAN 聚类(其中 DBSCAN 是基于密度的空间聚类的噪声应用程序)涉及在域中寻找高密度区域,并将其周围的特征空间区域扩展为群集。
它是通过 DBSCAN 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。
下面列出了完整的示例。
# dbscan 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import DBSCAN from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = DBSCAN(eps=0.30, min_samples=9) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,尽管需要更多的调整,但是找到了合理的分组。
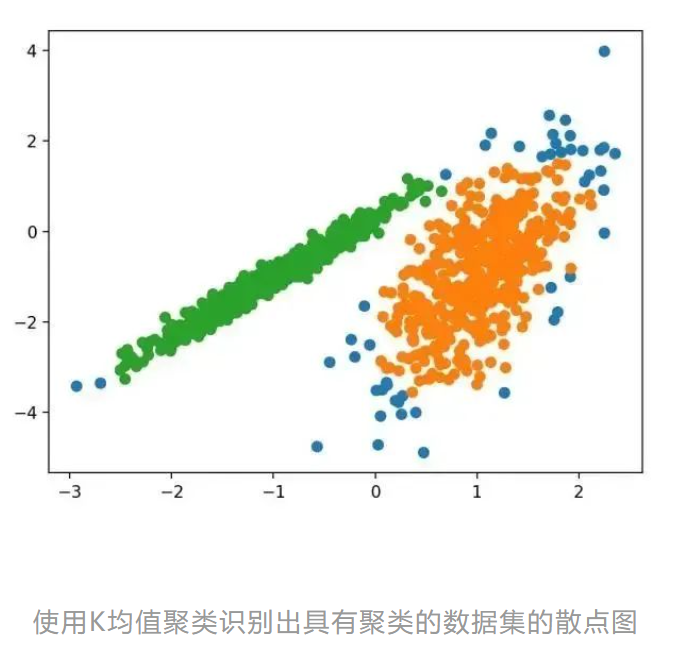
7.K均值
K-均值聚类可以是最常见的聚类算法,并涉及向群集分配示例,以尽量减少每个群集内的方差。
它是通过 K-均值类实现的,要优化的主要配置是“ n _ clusters ”超参数设置为数据中估计的群集数量。下面列出了完整的示例。
# k-means 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import KMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = KMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个合理的分组,尽管每个维度中的不等等方差使得该方法不太适合该数据集。
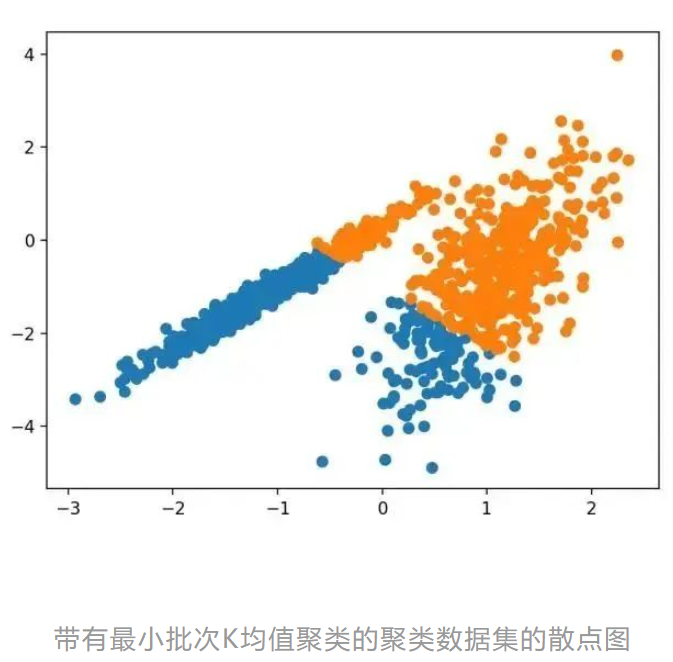
8.Mini-Batch K-均值
Mini-Batch K-均值是 K-均值的修改版本,它使用小批量的样本而不是整个数据集对群集质心进行更新,这可以使大数据集的更新速度更快,并且可能对统计噪声更健壮。
它是通过 MiniBatchKMeans 类实现的,要优化的主配置是“ n _ clusters ”超参数,设置为数据中估计的群集数量。下面列出了完整的示例。
# mini-batch k均值聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MiniBatchKMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MiniBatchKMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,会找到与标准 K-均值算法相当的结果。
9.均值漂移聚类
均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。
它是通过 MeanShift 类实现的,主要配置是“带宽”超参数。下面列出了完整的示例。
# 均值漂移聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MeanShift from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MeanShift() # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以在数据中找到一组合理的群集。
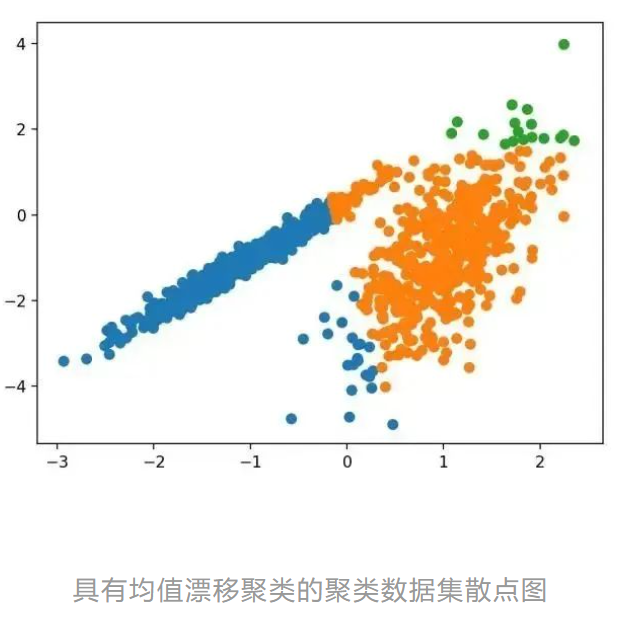
10.OPTICS
OPTICS 聚类( OPTICS 短于订购点数以标识聚类结构)是上述 DBSCAN 的修改版本。
它是通过 OPTICS 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。下面列出了完整的示例。
# optics聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import OPTICS from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = OPTICS(eps=0.8, min_samples=10) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,无法在此数据集上获得合理的结果。
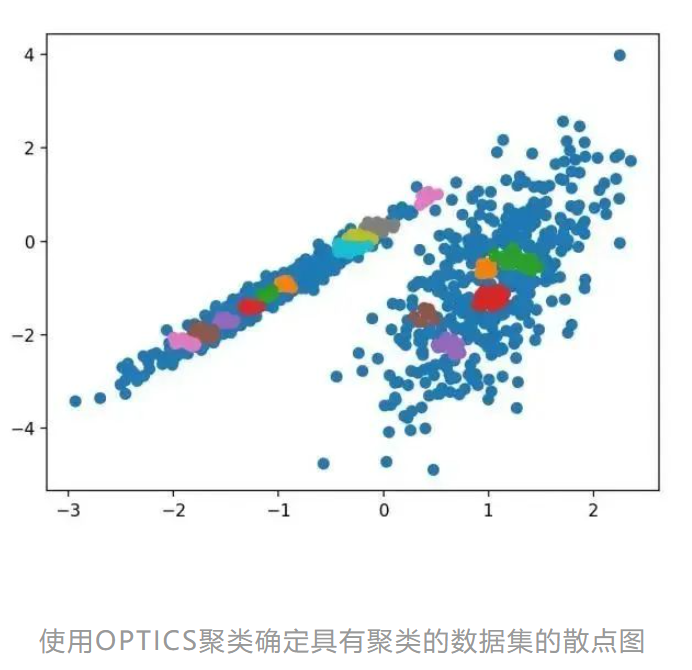
11.光谱聚类
光谱聚类是一类通用的聚类方法,取自线性线性代数。
它是通过 Spectral 聚类类实现的,而主要的 Spectral 聚类是一个由聚类方法组成的通用类,取自线性线性代数。要优化的是“ n _ clusters ”超参数,用于指定数据中的估计群集数量。下面列出了完整的示例。
# spectral clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import SpectralClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = SpectralClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,找到了合理的集群。
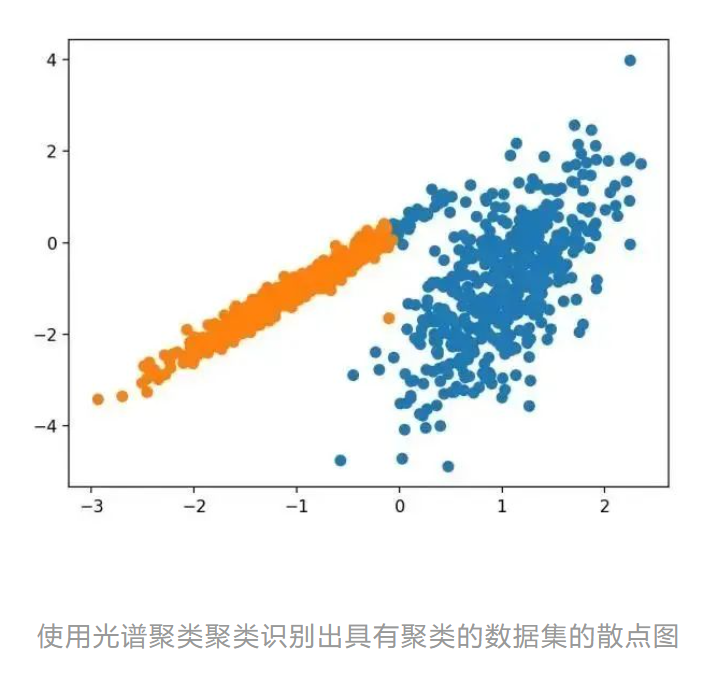
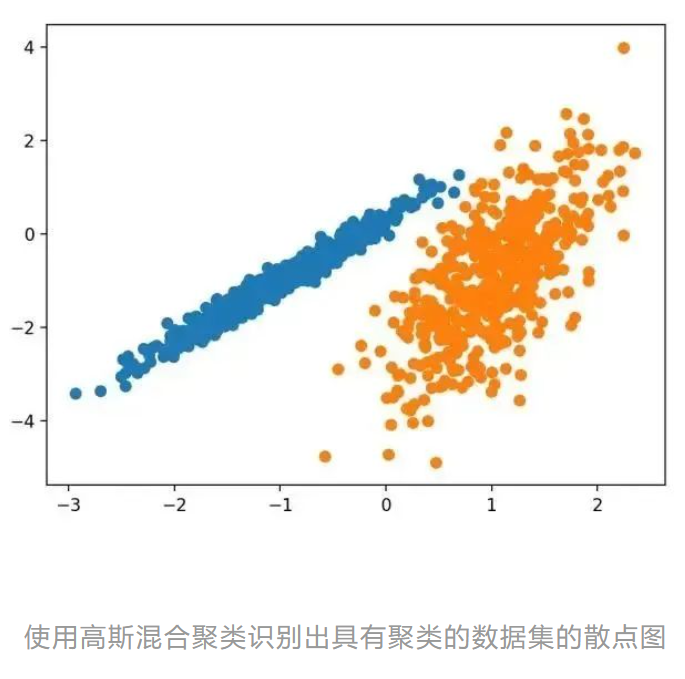
12.高斯混合模型
高斯混合模型总结了一个多变量概率密度函数,顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的,要优化的主要配置是“ n _ clusters ”超参数,用于指定数据中估计的群集数量。下面列出了完整的示例。
# 高斯混合模型 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.mixture import GaussianMixture from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = GaussianMixture(n_components=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,我们可以看到群集被完美地识别。这并不奇怪,因为数据集是作为 Gaussian 的混合生成的。