Codeforces Round #384 (Div. 2) 734E Vladik and cards

E. Vladik and cards

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Vladik was bored on his way home and decided to play the following game. He took n cards and put them in a row in front of himself. Every card has a positive integer number not exceeding 8 written on it. He decided to find the longest subsequence of cards which satisfies the following conditions:

• the number of occurrences of each number from 1 to 8 in the subsequence doesn't differ by more then 1 from the number of occurrences of any other number. Formally, if there are ck cards with number k on them in the subsequence, than for all pairs of integers 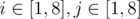 the condition |ci - cj| ≤ 1 must hold. 
• if there is at least one card with number x on it in the subsequence, then all cards with number x in this subsequence must form a continuous segment in it (but not necessarily a continuous segment in the original sequence). For example, the subsequence [1, 1, 2, 2] satisfies this condition while the subsequence [1, 2, 2, 1] doesn't. Note that [1, 1, 2, 2] doesn't satisfy the first condition. 

Please help Vladik to find the length of the longest subsequence that satisfies both conditions.

Input

The first line contains single integer n (1 ≤ n ≤ 1000) — the number of cards in Vladik's sequence.

The second line contains the sequence of n positive integers not exceeding 8 — the description of Vladik's sequence.

Output

Print single integer — the length of the longest subsequence of Vladik's sequence that satisfies both conditions.

Examples

input

3
1 1 1

output

1

input

8
8 7 6 5 4 3 2 1

output

8

input

24
1 8 1 2 8 2 3 8 3 4 8 4 5 8 5 6 8 6 7 8 7 8 8 8

output

17

Note

In the first sample all the numbers written on the cards are equal, so you can't take more than one card, otherwise you'll violate the first condition.

 

 

题意

给定一个序列an，序列中只有1~8的8个整数，让你选出一个子序列，满足下列两个要求

1.不同整数出现的次数相差小于或等于1

2.子序列中整数分布是连续的，即子序列的整数必须是1,1,1....1，2,2,2.....2,2.......连续分布，可以是任意顺序而不要求递增，比如312587644

 

dp[i][j]记录在j状态下前i个中长度位l个个数 答案就是 ans*l+（8-ans）*（l-1）。