差分约束算法总结

来自 https://blog.csdn.net/my_sunshine26/article/details/72849441

 

差分约束系统

一、概念

 

                  如果一个系统由n个变量和m个约束条件组成，形成m个形如ai-aj≤k的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统。

 

二、引例

 

给定n个变量和m个不等式，每个不等式的形式为 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m， a[k]已知)，求 x[i] - x[j] 的最大值。

例如当n = 4，m = 5，给出如下图所示的不等式组，求x3 - x0的最大值。

                                              

一般思路：我们可以尝试把几个不等式组合得到最后我们要求的式子，于是这些式子里最小的那个就是答案。

比如，在这个例子中：

（3） ==》  x3 - x0<=4；

（1）、（4）、（5） ==》 x3 - x0<=5；

（2）、（5） ==》 x3 - x0<=3;

所以最后结果就是3.

在这个过程中，我们是否想到这种方法与我们已经学的一种算法有所联系，是的，就是最短路算法。

 

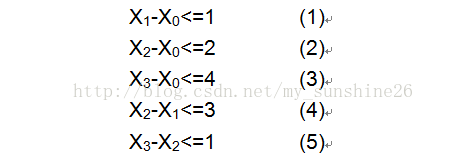
三、差分约束与最短路模型

 

1、与最短路模型的联系

 

先给出结论：求解差分约束系统，都可以转化成图论的单源最短路径（或最长路径）问题。

我们观察上面例子中的不等式，都是x[i] - x[j] <= a[k]，可以进行移项，成为x[i] <= x[j] + a[k]，我们令a[k] = w(j, i)，dis[i]=x[i],并使i=v,j=u,那么原始就变为：dis[u]+w(u,v)>=dis[v],于是可以联想到最短路模型中的一部分代码

1.  
   if(dis[u]+w(u,v)<=dis[v])
2.  
   {
3.  
   dis[v]=dis[u]+w(u,v);
4.  
   }

这不正与松弛操作相似吗？

但是好像不等号方向刚好相反，但其实这并不矛盾

上面的代码要实现的是使dis[u]+w(u,v)>dis[v],而对于不等式，我们进行建边的操作：对于每个不等式 x[i] - x[j] <= a[k]，对结点 j 和 i 建立一条 j -> i的有向边，边权为a[k]，求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路，两者刚好吻合。所以求解差分约束问题就转化为了最短路问题。

 

2.问题解的存在性

 

    由于在求解最短路时会出现存在负环或者终点根本不可达的情况，在求解差分约束问题时同样存在

 

    （1）、存在负环

 

如果路径中出现负环，就表示最短路可以无限小，即不存在最短路，那么在不等式上的表现即X[n-1] - X[0] <= T中的T无限小，得出的结论就是 X[n-1] - X[0]的最大值不存在。在SPFA实现过程中体现为某一点的入队次数大于节点数。（貌似可以用sqrt(num_node)来代替减少运行时间）

     （2）、终点不可达

这种情况表明X[n-1]和X[0]之间没有约束关系，X[n-1] - X[0]的最大值无限大，即X[n-1]和X[0]的取值有无限多种。在代码实现过程中体现为dis[n-1]=INF。

 

3、不等式组的转化

 

做题时可能会遇到不等式中的符号不相同的情况，但我们可以对它们进行适当的转化

（1）方程给出：X[n-1]-X[0]>=T ,可以进行移项转化为： X[0]-X[n-1]<=-T。

（2）方程给出：X[n-1]-X[0]<T, 可以转化为X[n-1]-X[0]<=T-1。

（3）方程给出：X[n-1]-X[0]=T，可以转化为X[n-1]-X[0]<=T&&X[n-1]-X[0]>=T，再利用（1）进行转化即可

 

4、应用

 

对于不同的题目，给出的条件都不一样，我们首先需要关注问题是什么，如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成"<="的形式，建图后求最短路；相反，如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成">="，建图后求最长路。

 

5、相关题目链接

 

（1）、POJ 1716 Integer Intervals 

（2）、HDOJ 3666 THE MATRIX PROBLEM  

--------------------- 本文来自 Dust_Heart 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/my_sunshine26/article/details/72849441?utm_source=copy