cf1058E 思维 前缀处理 位运算

题目大意：给定一个长度为 (n≤3×105)的数列ai(1≤ai≤10 18) 可以交换序列中一个数的任意二进制位的位置，问你可以选出多少区间经过操作后异或和是 0 

链接：http://codeforces.com/contest/1058/problem/E

 

思路：由于二进制随意交换，那么它本身值不必考虑，只需要保存它有多少二进制为1的个数就好了。

区间异或和为0 的充分必要条件：

• 区间中二进制1的个数是偶数
• 区间中二进制位最多的一个数的二进制个数1的个数  小于等于 1总和的一半

对于条件一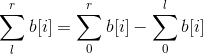 

所以前面的为偶数的前提下  ， 根据（0，l）的奇偶性 来判断 (l,r)的奇偶性  所以 ，将所有前缀和的奇偶性统计出来  O(n)的负责度

暂且将条件一全加上  然后再在条件二中减去

因为a[i]<=1e18  且 >=1 的限制

所以在删除条件二的时候，最大的数不过63，最小的为1， 那么枚举60多次就可以截至  

 

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define pb push_back
#define fi first
#define se second
#define all(v) v.begin(),v.end()
#define forn(i,a,n) for(int i=a;i<n;++i)


const int N = 3e5+4;
ll a[N],b[N];

ll cbit(ll x){
    ll res=1;
    while(x){
        if(x&1)res++;
        x/=2;
    }
    return res-1;
}
ll sum[N];
int cnt[2];

int main(){

    int n;
    cin>>n;
    forn(i,1,n+1){
        scanf("%lld",a+i);
        b[i]= cbit(a[i]);
    }
    ll ans=0 ;

    cnt[0]=1;

    forn(i,1,n+1){
        sum[i] = sum[i-1]+b[i];
　　　　　//条件一 全部加上，也就是 sum[r]-sum[l]%2==0的所有 （l属于0~r-1），其实完全可以根据sum[r]的奇偶性进行判断
　　　　　 //这也就是与sum[r] 同样奇偶性的数量了

        ans += cnt[sum[i]&1]; 
       
　　　　 //根据条件2 倒着减过去  将同样为偶数1 但是最大值不满足条件的减去
        int j =i,k=i;
        ll  Max = b[i];

        while(k>=1 && j-k<=62 ){
            Max = max(Max,b[k]);
           if(  Max*2 > sum[i]-sum[k-1] && ( (sum[i]-sum[k-1] )%2==0 )  )ans--;
           k--;
        }
        cnt[sum[i]&1]++;
        //cout<<ans<<endl;

    }

    cout<<ans<<endl;

    return 0;
}

 

---恢复内容结束---