OpenCV计算机视觉学习（16）——仿射变换学习笔记

如果需要其他图像处理的文章及代码，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/ComputerVisionPractice

　　在计算机视觉和图像处理中，仿射变换是一种重要的几何变换方法。它可以通过线性变换和平移来改变图像的形状和位置，广泛应用与图像校正，对象识别以及增强现实等领域。

　　最近对OpenCV的仿射变换和逆仿射变换的算子使用较多，觉得有必要再整理一篇笔记，学习一下其原理，同时在一些实际场景的应用。下面首先学习一下其原理及其数学推导，然后我再试试在OpenCV中的应用。

1，仿射变换原理

　　毫无疑问，仿射变换（Affine Transformation）是线性代数和几何学中的一个重要概念。它是指在二维或三维空间中，通过线性变换和平移来改变对象的位置和形状，保持原有对象的直线性和平移性。即二维图形之间的相对位置保持不变，平行线依然是平行线，且直线上的点的位置顺序不变。一个任意的仿射变换都可以表示为乘以一个矩形再加上一个向量的形式。它可以实现平移（translation 向量加法）、旋转（rotation 线性变换）、缩放（scale 线性变换）和剪切（sheer )等操作。仿射变换通过对图像中的每个像素应用线性变换矩阵来实现，从而改变图像的位置、大小和方向。

　　以下是仿射变换的一般原理：在二维空间中，仿射变换是使用一个 2x3 的线性变换矩阵来描述变换操作。矩阵的前两列代表旋转、缩放和剪切操作，而最后一列代表平移操作。正如上面概念所说，矩阵的前两列是乘法，后一列是加法。

　　线性变换矩阵如下所示：

[ a  b  tx ]
[ c  d  ty ]

• a 和 d 控制缩放和旋转。
• b 和 c 控制剪切。
• tx 和 ty 控制平移。

　　如果说直接看上面变换矩阵有些抽象的话，我们可以推导一下其公式，做到知其然，知其所以然。

1.1 仿射变换的公式及其推导

　　假设我们有一个二维空间中的点 p=(x, y），并且我们想要应用一个仿射变换到这个点上。仿射变换通常可以表示为以下形式：

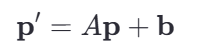
 　　这里 P` = (x`, y`) 是变换后的点。A是一个 2*2 的矩阵，代表线性变换部分。b=(bx, by) 是一个平移向量。然后我们将仿射变换分为线性变换部分和平移部分。也就是上面的a,b,c,d和 tx, ty。下面先说线性变换部分：

线性变换部分

 　　线性变换可以用一个 2*2 的矩阵来表示，该矩阵可以旋转，缩放或剪切一个图像。假设矩阵A为：

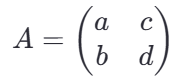
 　　对于一个点 p=(x, y)，线性变换的结果为：

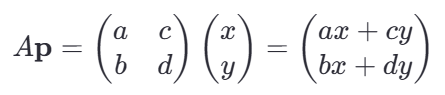
平移部分

　　平移操作是简单的坐标偏移，可以通过向量加法实现。如果我们要将一个点 p 平移到一个新的位置，只需要简单的加上一个平移向量 b：

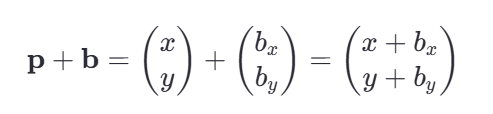
合并线性变换和平移部分

　　要合并这两个操作，我们可以先进行线性变换，然后进行平移操作：

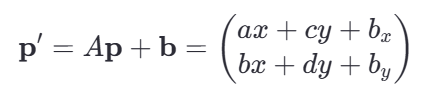
 　　然后使用齐次坐标表示：

 　　为了方便地用矩阵表示包含平移的仿射变换，我们使用齐次坐标系。齐次坐标系中，二维空间中的点 (x, y) 被表示为 (x, y, 1)形式的三元组。这样，我们可以将仿射变换写成一个 3*3 矩阵乘法的形式：

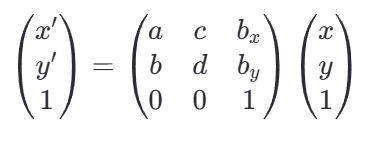
 　　这种表示方法允许我们将线性变换和平移操作统一在一个矩阵运算中完成，简化了计算过程。

 　　乘法结果为：

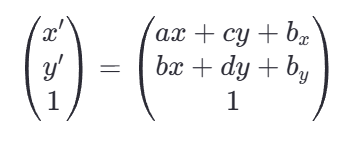
 　　这意味着变换后的点的坐标为 （ax + cy + bx, bx +dy +by)。

 

1.2 实际应用变换

　　下面看一个实际应用的示例。对于每个输入图像中的像素 (x, y)，应用仿射变换矩阵可以得到变换后的像素 (x', y')，计算如下：

x' = a * x + b * y + tx
y' = c * x + d * y + ty

　　这些计算会将输入图像中的每个像素映射到输出图像的相应位置。

　　下面我们仍然将其拆解开，假设我们有矩阵 A 和向量 b 如下：

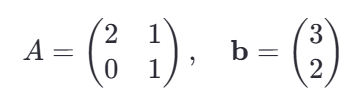
　　线性变换可以通过矩阵 A 来表示，矩阵 A 可以实现各种操作，比如旋转，缩放，剪切等。矩阵A的选择具体取决于你想要实现的具体变换类型。例如上面矩阵A就是将实现一个缩放和平行四边形的变换。具体来说，它会使得 x 坐标翻倍，并且在 x方向上增加一半的 y 值。

　　而平移变换通过向量b来实现，它是一个简单的坐标便宜。如果 b=(3, 2), 那么所有点都会沿着 x 方向移动 3个单元，沿 y方向移动 2 个单位。

 　　对于点 p=(1, 2) 应用仿射变换，我们将上述两部分结合在一起，实现一个完整的仿射变换。即应用上面提到的矩阵A和向量 b到这个点上。按照仿射变换的公式，我们有：

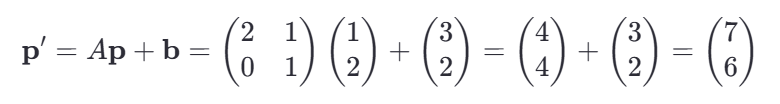
 　　因此变换后的点坐标为 (7, 6)。所以这就是仿射变换。

　　所以说，仿射变换就是两幅图像之间的一种联系，关于这种联系的信息大致可以分为以下两种场景：

　　1，已知图像A和变换矩阵M，求图像B，只需要应用B=M*A即可，也就是上面的公式，只是我们只求了一个点而已。

　　2，已知图像A和图像B，而且已知他们是有联系的，接下来就是求出矩阵M。

 

1.3 仿射变换的插值问题

　　在图像进行仿射变换时，原图像的像素点可能不会精确对应到变换后图像的像素网格上。这就引入了插值的问题，因为我们需要确定变换后图像中每个像素的颜色值，即使这些像素可能位于原图像中像素点之间的位置。

　　在实际应用中，变换后的像素位置可能不是整数值，因此需要使用插值方法来获取非整数坐标上的像素值。插值是估算连续函数在已知数据点之间未知值的过程。

　　在图像变换中，常用的插值方法包括最近邻插值、双线性插值和三次样条插值。

最近邻插值（Nearest Neighbor Interpolation）：其选择最接近变换后坐标的原始像素值，它是最简单的插值方法，为每个目标像素分配最接近源像素的颜色值，这种方法计算效率高，但可能会导致变换后的图像出现明显的锯齿状边缘。

双线性插值(Bilinear Interpolation)：通过在四个最近的像素之间进行插值来计算像素值。根据目标像素与这四个源像素的相对距离来加权平均计算目标像素的颜色值。这种方法可以减少锯齿现象，使图像看起来更加平滑。

双三次样条插值（Bicubic Interpolation）：使用更复杂的插值算法，产生更平滑的结果。它考虑了更多的相邻像素，并使用三次多项式来估算目标像素的颜色值。这种方法可以产生更高质量的图像，但计算成本也更高。

　　在应用仿射变换时，插值的一般过程如下：

逆变换：应用仿射变换的逆变换，将目标图像的像素坐标映射回源图像的坐标系统中。这是因为我们需要根据源图像的像素值来确定目标图像的像素值。

查找源像素：对于目标图像中的每个像素，找到其在源图像中的对应未知。由于仿射变换可能产生非整数坐标，因此需要进行插值。

插值计算：根据选定的插值方法（如最近邻，双线性或双三次插值），计算目标像素的颜色值。这通常涉及到对周围像素颜色值的加权平均。

赋值：将计算得到的颜色值赋给目标图像的相应像素。

 　　在进行插值时，需要注意边界条件。当源像素坐标落在原图像边界之外时，需要采取适当的处理措施，如使用边缘像素的重复、镜像或设置为特定颜色。

　　此外，插值算法的复杂度和计算成本也是选择插值方法时需要考虑的因素。通常，双线性插值是一个折衷的选择，它提供了较好的图像质量和合理的计算效率。

　　总之，插值是仿射变换中不可或缺的一部分，它确保了变换后的图像质量，避免了像素失真和锯齿效应。

 

1.4 仿射变换应用顺序

　　在进行多个仿射变换时，他们的顺序会影响最终结果。例如，先进行旋转再进行平移和先进行平移再进行旋转，可能会得到不同的结果，所以这点要注意。

　　仿射变换在计算机视觉和图像处理中具有广泛的应用，如图像校正，图像配准，图像扭曲和增强等。

　　总之，仿射变换是通过线性变换矩阵将图像进行平移、旋转、缩放和剪切等操作的技术，它可以在图像处理中实现多种形式的变换和调整。

 

2， OpenCV中的仿射变换实现

　　在OpenCV中，仿射变换的实现非常简单，我们可以使用 cv2.getAffineTransform()函数等获取仿射变换的矩阵，并通过 cv2.warpAffine()函数应用变换。

2.1  warpAffine()函数

　　warpAffine()函数的是OpenCV的一个函数，用于执行仿射变换。仿射变换是一种线性变换，正如上面所提到的，它包含旋转，缩放，错切和平移。warpAffine()函数接收一个输入图像和一个变换矩阵，然后应用这个变换矩阵来生成输出图像。

　　正如上面提到的，该变换矩阵是一个2*3的矩阵，由一个2*2的线性变换矩阵和一个2*1的平移向量组成，变换矩阵的形式如下（我知道我啰嗦了，但是我只是想让自己记下）：

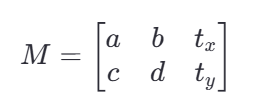
 　　操作的话，首先通过需要的变换类型（如旋转，缩放，平移等）来计算变换矩阵。OpenCV提供了getRotationMatrix2D()等函数来帮助我们计算这些矩阵。

　　然后使用wrapAffine()函数，将计算得到的变换矩阵应用于输入图像。我们可以选择输出的图像大小和插值方法。

　　warpAffine() 函数的基本语法如下：

cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])

 　　参数：

• src：输入图像。
• M：2×3 的仿射变换矩阵。
• dsize：输出图像的大小，是一个二元组 (width, height)。
• dst：可选参数，用于指定输出图像。
• flags：插值方法，默认为 INTER_LINEAR。
• borderMode：边界处理方法，默认为 BORDER_CONSTANT。
• borderValue：边界填充值，默认为 0。

　　通过这个函数，你可以轻松地对图像进行各种仿射变换操作，如旋转、缩放、倾斜和位移等。

　　下面是一个使用warpAffine()的示例，演示如何旋转一张图像：

import cv2
import numpy as np
 
# 读取图片
img = cv2.imread('george.png')
 
# 图像中心
rows, cols = img.shape[:2]
center = (cols / 2, rows / 2)

# 计算旋转矩阵
angle = 45  # 旋转角度
scale = 1.0  # 缩放比例
M = cv2.getRotationMatrix2D(center, angle, scale)
 
# 应用仿射变换
dst = cv2.warpAffine(img, M, (cols, rows))
 
# 保存结果
# cv2.imwrite('output.jpg', dst)
# 显示结果
cv2.imshow('Rotated Image', dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　结果如下：

 

 2.2  getRotationMatrix2D()函数

　　getRotationMatrix2D 是 OpenCV 库中的一个函数，用于计算围绕某个中心点的旋转矩阵。这个函数特别有用，当你需要在图像处理或计算机视觉任务中旋转图像时，例如为了校正倾斜的文本或调整视角。

 　　函数的基本语法如下：

cv::Mat cv::getRotationMatrix2D(const Point2f& center, double angle, double scale);

 　　参数解释：

• center: 旋转中心的坐标，通常是一个 (x, y) 的二元组，表示图像中旋转轴的中心点。
• angle: 旋转的角度，单位是度。正数表示逆时针方向旋转，负数表示顺时针方向旋转。
• scale: 缩放因子。当 scale 等于 1 时，表示没有缩放，图像大小不变；大于 1 表示放大；小于 1 表示缩小。

　　返回值：函数返回一个 2x3 的仿射变换矩阵，该矩阵可以用于 warpAffine 或 warpPerspective 函数来对图像进行旋转。矩阵的形式如下：

 　　其中 Θ 是旋转角度， tx 和 ty 是平移分量，，用于确保图像围绕指定的中心点旋转。

 　　下面说一个使用示例。假设我们有一个图像，并且你想要围绕图像的中心点旋转 45 度，同时保持图像大小不变（即缩放因子为 1）。以下是使用 Python 和 OpenCV 的示例代码：

import cv2
import numpy as np

# 加载图像
image = cv2.imread('george.png')

# 获取图像尺寸
height, width = image.shape[:2]

# 计算旋转中心
center = (width / 2, height / 2)

# 定义旋转角度和缩放因子
angle = 45
scale = 1.0

# 获取旋转矩阵
rotation_matrix = cv2.getRotationMatrix2D(center, angle, scale)

 　　在这个例子中，我们首先计算了图像的中心点，然后使用 getRotationMatrix2D 函数得到了旋转矩阵。我打印了以下其旋转矩阵如下：

[[   0.70710678    0.70710678 -114.85921677]
 [  -0.70710678    0.70710678  208.70532111]]

 　　最后就是使用这个旋转矩阵在wrapAffine()函数中。

 

2.3  getAffineTransform()函数

　　cv2.getAffineTransform() 是 OpenCV 中的一个函数，用于计算一个仿射变换矩阵，该矩阵可以将源图像中的一个三角形区域映射到目标图像中的另一个三角形区域。仿射变换可以包括旋转、缩放、错切（shear）和平移。

　　函数定义如下：

cv2.getAffineTransform(src, dst)

 　　参数如下：

• src: 这是一个 3x2 的浮点型 NumPy 数组，包含源图像中的三个点。这三个点定义了源三角形。
• dst: 这也是一个 3x2 的浮点型 NumPy 数组，包含目标图像中的三个点，这些点与 src 中的点一一对应。

　　返回值如下：函数返回一个 2x3 的浮点型矩阵，这就是仿射变换矩阵，可以用于通过 cv2.warpAffine() 函数对图像应用仿射变换。

 　　计算原理：仿射变换矩阵A由以下方程定义：

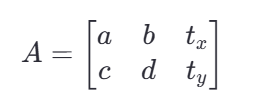
 　　其中 tx, ty是平移向量，而 a, b, c, d定义了线性变换部分。

使用示例：假设我们有一张图像，并且我们想要通过仿射变换将图像中某一部分的三个角点映射到另一组三个角点上。以下是使用 Python 和 OpenCV 的示例代码：

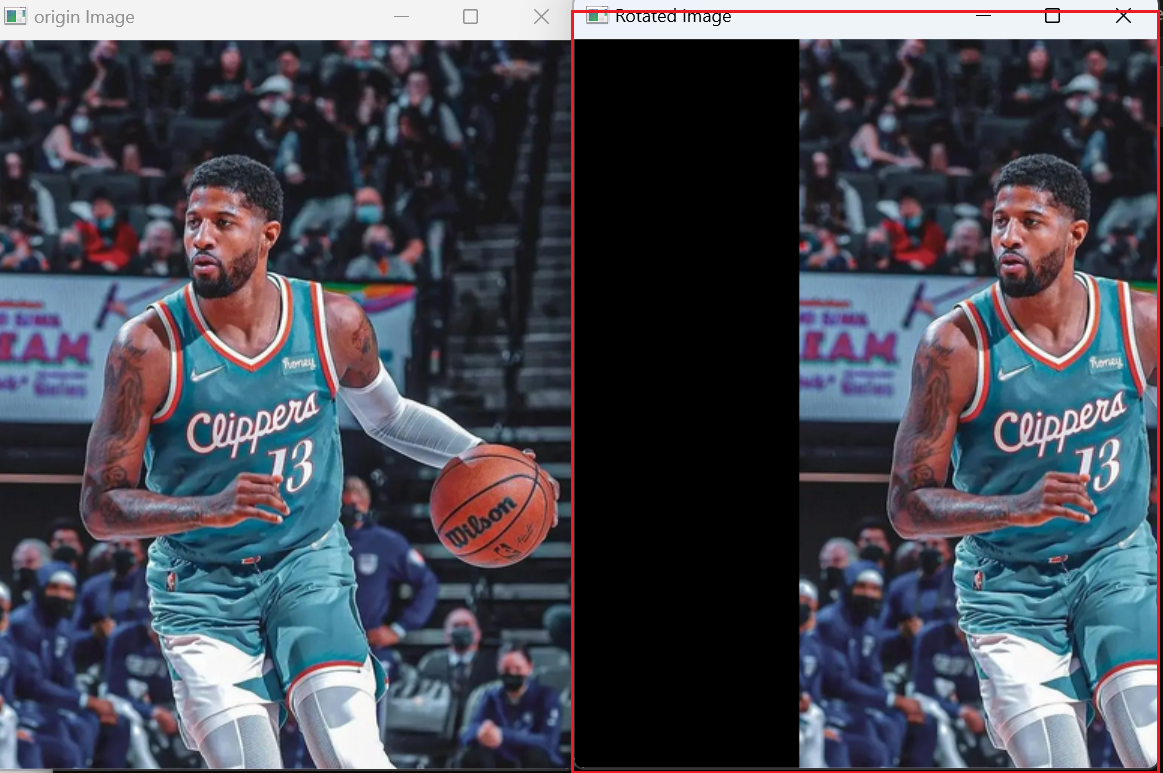
import cv2
import numpy as np

# 加载图像
image = cv2.imread('george.png')

# 定义源三角形的三个角点
src_points = np.float32([[0, 0], [300, 0], [0, 300]])

# 定义目标三角形的三个角点
dst_points = np.float32([[150, 0], [450, 0], [150, 300]])

# 计算仿射变换矩阵
affine_matrix = cv2.getAffineTransform(src_points, dst_points)

print("affine_matrix is ", affine_matrix)

# 应用仿射变换
transformed_image = cv2.warpAffine(image, affine_matrix, (image.shape[1], image.shape[0]))

# 显示结果
cv2.imshow('origin Image', image)
cv2.imshow('Rotated Image', transformed_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　在这个例子中，我们定义了源图像和目标图像中三角形的三个角点，然后使用 cv2.getAffineTransform() 函数计算仿射变换矩阵，最后使用 cv2.warpAffine() 函数将变换应用到整个图像上。　

　　我也打印了这个变换矩阵，很明显只是平移而已：

[[  1.   0. 150.]
 [  0.   1.   0.]]

 　　我们看看最终图像：

 

2.4  getAffineTransform和getRotationMatrix2D 的区别

　　看到上面两个函数及其用法，估计大家也可以出个七七八八，我就再啰嗦以下其区别。

　　cv2.getAffineTransform() 和 cv2.getRotationMatrix2D() 都是 OpenCV 中用于计算变换矩阵的函数，但它们的目的和使用场景有所不同。下面是两者的主要区别：

cv2.getAffineTransform()

• 功能：getAffineTransform() 用于计算一个从源图像中的一个三角形到目标图像中另一个三角形的仿射变换矩阵。这个矩阵可以实现旋转、缩放、错切和/或平移的组合。
• 参数：函数接受两个参数，每个参数都是一个 3x2 的浮点型 NumPy 数组，分别表示源三角形和目标三角形的三个顶点坐标。
• 用途：通常用于矫正图像中特定区域的透视变形，比如将一个扭曲的矩形区域校正为标准矩形。

cv2.getRotationMatrix2D()

• 功能：getRotationMatrix2D() 主要用于计算围绕一个特定点的旋转矩阵，同时可以包含缩放操作。这个函数专注于旋转和缩放变换，不涉及错切。
• 参数：函数接受三个参数，分别是旋转中心的坐标（x, y）、旋转角度（以度为单位）和缩放因子。
• 用途：通常用于图像旋转，比如纠正图像中的倾斜角度，或为了改变图像视角而进行的旋转。

主要区别

• 变换类型：getRotationMatrix2D() 专注于旋转和缩放，而 getAffineTransform() 可以实现更复杂的仿射变换，包括错切。
• 参数输入：getRotationMatrix2D() 需要指定旋转中心、角度和缩放因子，而 getAffineTransform() 通过源三角形和目标三角形的顶点坐标来定义变换。
• 适用场景：getRotationMatrix2D() 更适合需要精确控制旋转角度和缩放的应用，而 getAffineTransform() 适用于需要校正或匹配图像中特定区域形状的情况。

　　 总结而言，getRotationMatrix2D() 提供了一种简便的方式来实现旋转和缩放变换，而 getAffineTransform() 则提供了更通用的仿射变换能力，适用于需要同时处理旋转、缩放、错切和平移的复杂场景。