OpenCV计算机视觉学习（12）——图像量化处理&图像采样处理（K-Means聚类量化，局部马赛克处理）

如果需要处理的原图及代码，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/ComputerVisionPractice

准备：图像转数组，数组转图像

　　将RGB图像转换为一维数组的代码如下：

# 图像二维像素转换为一维
img = cv2.imread(filename=img_path)
data = img.reshape((-1, 3))
data = np.float32(data)
print(img.shape, data.shape)

 　　我们打印出来结果，看看如下：

(67, 142, 3) (9514, 3)

 　　当我们处理完后，再将图像转换回uint8二维类型，代码如下：

# 图像转换回uint8二维类型
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))

# 图像转换为RGB显示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

 

1，图像量化处理

　　图像通常是自然界景物的客观反映，并以照片形式或视频记录的介质连续保存，获取图像的目标是从感知的数据中产生数字图像，因此需要把连续的图像数据离散化，转换为数字化图像，其工作主要包括两方面——量化和采样。数字化幅度值称为量化，数字化坐标值称为采样。

　　下面主要学习图像量化和采样处理的概念，并通过Python和OpenCV实现这些功能。

1.1  图像量化概述

　　所谓量化（Quantization），就是将图像像素点对应亮度的连续变换区间转换为单个特定值的过程，即将原始灰度图像的空间坐标幅度值离散化。量化等级越多，图像层次越丰富，灰度分辨率越高，图像的质量也越好；量化等级越少，图像层次欠丰富，灰度分辨率越低，会出现图像轮廓分层的现象，降低了图像的质量，下图是将图像的连续灰度值转换为0到255的灰度级的过程。

　　量化后，图像就被表示成一个整数矩阵，每个像素具有两个属性：位置和灰度。位置由行，列表示。灰度表示该像素位置上亮暗程度的整数。此数字矩阵M*N就作为计算机处理的对象了，灰度级一般为0~255（8bit量化）。如果量化等级为2，则将使用两种灰度级表示原始图像的像素（0~255），灰度值小于128的取0，大于等于128的取128；如果量化等级为4，则将使用四种灰度级表示原始图像的像素，新图像将分层为四种颜色，0~64区间取0,64~128区间取64,128~192区间的取128,192~255区间取192，依次类推。

1.1.1  图像彩色量化（减色处理）简介

　　RGB 的像素值在 0~255之间，我们想要用更少的内存空间表征一张图像时怎么办呢？首先是减色处理，将图像用 32， 96， 160， 224 这 4 个像素值表示。即将图像由256³压缩至4³，RGB的值只取{32,96,160,224}，这被称作色彩量化。

1.2  图像量化的代码实现

　　下面学习Python图像量化处理相关代码凑在哦，其核心流程是建立一张临时图片，接着循环遍历原始图像中所有像素点，判断每个像素点应该属于的量化等级，最后将临时图像展示，下面代码学习将灰度图像转换为两种量化等级。

　　代码如下：

#_*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('kd2.jpg')
# 获取图像的高度和宽度
height, width = img.shape[0], img.shape[1]

# 创建一幅图像，内容使用零填充
new_img = np.zeros((height, width, 3), np.uint8)

# 图像量化操作，量化等级为2
for i in range(height):
    for j in range(width):
        for k in range(3):  # 对应BGR三通道
            if img[i, j][k] < 128:
                gray = 0
            else:
                gray = 129
            new_img[i, j][k] = np.uint8(gray)

# 显示图像
cv2.imshow('src', img)
cv2.imshow('new', new_img)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　下图是输出结果，它将图像划分为两种量化等级。

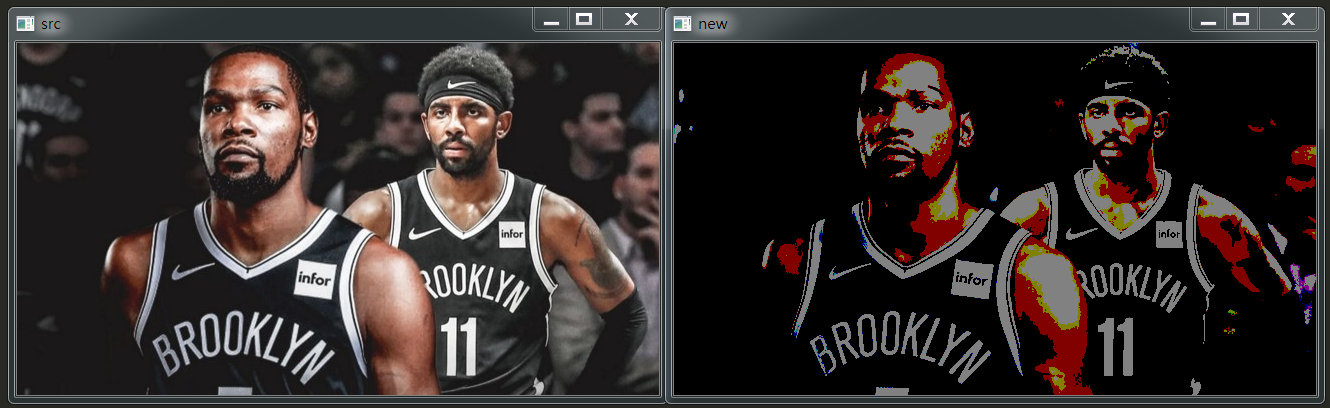
 　　下面的代码分别比较了量化等级为2， 4， 8 的量化处理效果。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('kd2.jpg')
# 获取图像的高度和宽度
height, width = img.shape[0], img.shape[1]

# 创建一幅图像，内容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)
new_img2 = np.zeros((height, width, 3), np.uint8)
new_img3 = np.zeros((height, width, 3), np.uint8)

# 图像量化操作，量化等级为2
for i in range(height):
    for j in range(width):
        for k in range(3):  # 对应BGR三通道
            if img[i, j][k] < 128:
                gray = 0
            else:
                gray = 129
            new_img1[i, j][k] = np.uint8(gray)

# 图像量化操作，量化等级为4
for i in range(height):
    for j in range(width):
        for k in range(3):  # 对应BGR三通道
            if img[i, j][k] < 64:
                gray = 0
            elif img[i, j][k] < 128:
                gray = 64
            elif img[i, j][k] < 192:
                gray = 128
            else:
                gray = 192
            new_img2[i, j][k] = np.uint8(gray)

# 图像量化操作，量化等级为8
for i in range(height):
    for j in range(width):
        for k in range(3):  # 对应BGR三通道
            if img[i, j][k] < 32:
                gray = 0
            elif img[i, j][k] < 64:
                gray = 32
            elif img[i, j][k] < 96:
                gray = 64
            elif img[i, j][k] < 128:
                gray = 96
            elif img[i, j][k] < 160:
                gray = 128
            elif img[i, j][k] < 192:
                gray = 160
            elif img[i, j][k] < 224:
                gray = 192
            else:
                gray = 224
            new_img3[i, j][k] = np.uint8(gray)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图像
titles = [u'(a)原始图像', u'(b)量化L2', u'(c)量化L4', u'(d)量化L8', ]
images = [img, new_img1, new_img2, new_img3]
for i in range(4):
    plt.subplot(2, 2, i+1), plt.imshow(images[i])
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　结果如下：

1.3，图像分割与聚类概述

1.3.1  图像分割的定义

　　图像分割是图像识别和计算机视觉至关重要的预处理方法。图像分割就是把图像分成若干个特定的，具有独特性质的区域并提出感兴趣目标的技术和过程。它是由图像处理到图像分析的关键步骤。现有的图像分割方法主要分为以下几类：基于阈值的分割方法，基于区域的分割方法，基于边缘的分割方法以及基于特定理论的分割方法等。从数学角度来看，图像分割是将数字图像划分成互不相交的区域的过程。图像分割的过程也是一个标记过程，即把属于同一区域的像素赋予相同的编号。

1.3.2  聚类的定义

　　一个聚类就是一组数据对象的集合，集合内各对象彼此相似，各集合间的对象彼此相差较大。将一组物理或抽象对象中类似的对象组织成若干组的过程就称为聚类过程。然而在聚类的过程中，我们涉及到的对象的数据类型除了常用的间隔数值属性，二值属性，符号，顺序，比例数值属性，混合类型属性等外，还可能遇到图像，音频，视频等多媒体数据对象。对于传统的数据类型已经有了很多成熟的计算距离方法，这些方法包括：欧式，Manhattan，Minkowski距离公式，二值变量距离比较公式等等。然而对于多媒体数据对象，由于其特殊性，一致没有一个很好地算法对其进行分类。

　　聚类是一个将数据集划分为若干簇或类的过程，并使得同一簇内的数据对象具有较高的相似度，而不同组中的数据对象则是不相似的。相似或不相似的度量是基于数据对象描述属性的取值来确定的。通常是利用（各对象间）距离来进行描述。

　　下面要学习的是基于理论的图像图像分割方法，通过 K-Means聚类算法实现图像分割或颜色分层处理。

1.4，K-Means 聚类量化处理

1.4.1  K-Means 聚类量化处理原理

　　K-Means 聚类是最常用的聚类算法，最初起源于信号处理，其目的是将数据点划分为 K 个类簇，找到每个簇的中心并使其度量最小化。该算法的最大优点是简单，便于理解，运算速度较快，缺点是只能应用于连续性数据，并且要在聚类前指定聚类的类簇数。

　　如果想了解K-Means算法的原理，请参考我这篇博客：

Python机器学习笔记：K-Means算法，DBSCAN算法

　　下面是 K-Means 聚类算法的分析流程，步骤如下：

• 第一步，确定K值，即将数据集聚集成K个类簇或小组。
• 第二步，从数据集中随机选择K个数据点作为质心（Centroid）或数据中心。
• 第三步，分别计算每个点到每个质心之间的距离，并将每个点划分到离最近质心的小组，跟定了那个质心。
• 第四步，当每个质心都聚集了一些点后，重新定义算法选出新的质心。
• 第五步，比较新的质心和老的质心，如果新质心和老质心之间的距离小于某一个阈值，则表示重新计算的质心位置变化不大，收敛稳定，则认为聚类已经达到了期望的结果，算法终止。
• 第六步，如果新的质心和老的质心变化很大，即距离大于阈值，则继续迭代执行第三步到第五步，直到算法终止。

　　下图是对身高和体重进行聚类的算法，将数据集的人群聚类成三类。

1.4.2  K-Means 聚类opencv源码

　　在opencv中，KMeans() 函数原型如下所示：

retval, bestLabels, centers = kmeans(data, K, bestLabels, criteria, attempts, 
flags[, centers])

　　函数内变量的含义：

• data表示聚类数据，最好是np.flloat32类型的N维点集，之所以是 np.float32 原因是这种数据类型运算速度快，同样的数据下如果是 uint型数据将会特别慢。
• K表示聚类类簇数，opencv的kmeans分类是需要已知分类数的。
• bestLabels表示预设的分类标签，即输出的整数数组，用于存储每个样本的聚类标签索引，没有的话为None
• criteria表示算法终止条件，即最大迭代次数或所需精度。在某些迭代中，一旦每个簇中心的移动小于criteria.epsilon，算法就会停止，迭代停止的选择是一个含有三个元素的元组型数，格式为（type,  max_iter, epsilon），其中 type 有两种选择：

　　　　——cv2.TERM_CRITERIA_EPS：精确度（误差）满足 epsilon停止

　　　　——cv2.TERM_CRITERIA_MAX_ITER：迭代次数超过 max_iter 停止

　　　　——cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER，两者合体，任意一个满足结束。

• attempts表示重复试验kmeans算法的次数，算法返回产生最佳紧凑性的标签
• flags表示初始中心的选择，两种方法是cv2.KMEANS_PP_CENTERS ;和cv2.KMEANS_RANDOM_CENTERS
• centers表示集群中心的输出矩阵，每个集群中心为一行数据

1.4.3  K-Means 聚类分割灰度图像

　　在图像处理中，通过 K-Means聚类算法可以实现图像分割，图像聚类，图像识别等操作，下面主要用来进行图像颜色分割。假设存在一张 100*100像素的灰度图像，它由 10000 个RGB灰度级组成，我们通过 K-Menas 可以将这些像素点聚类成 K 个簇，然后使用每个簇内的置心点来替换簇内所有的像素点，这样就能实现在不改变分辨率的情况下量化压缩图像颜色，实现图像颜色层级分割。

　　下面使用该方法对灰度图像颜色进行分割处理，需要注意，在进行 K-Means 聚类操作之前，需要将 RGB像素点转换成一维的数组，再讲各形式的颜色聚集在一起，形成最终的颜色分割。

# _*_coding:utf-8_*_
# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取原始图像灰度颜色
img = cv2.imread('scenery.jpg', 0)
print(img.shape)

# 获取图像高度、宽度
rows, cols = img.shape[:]

# 图像二维像素转换为一维
data = img.reshape((rows * cols, 1))
data = np.float32(data)

# 定义中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 设置标签
flags = cv2.KMEANS_RANDOM_CENTERS

# K-Means聚类 聚集成4类
compactness, labels, centers = cv2.kmeans(data, 4, None, criteria, 10, flags)

# 生成最终图像
dst = labels.reshape((img.shape[0], img.shape[1]))

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图像
titles = [u'灰度图像', u'聚类图像']
images = [img, dst]
for i in range(2):
    plt.subplot(1, 2, i + 1), plt.imshow(images[i], 'gray'),
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　原图如下：

 　　输出结果如下所示，左边为灰度图，右边为K-Means聚类后的图像，它将相似的颜色或区域聚集到一起。

 　　人物图如下：

 　　效果如下：

1.4.4  K-Means 聚类对比分割彩色图像

　　下面代码是对彩色图像进行颜色分割处理，它将彩色图像聚类成2类，4类和64类。

# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取原始图像
img = cv2.imread('scenery.jpg')
print(img.shape)

# 图像二维像素转换为一维
data = img.reshape((-1, 3))
data = np.float32(data)

# 定义中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# 设置标签
flags = cv2.KMEANS_RANDOM_CENTERS

# K-Means聚类 聚集成2类
compactness, labels2, centers2 = cv2.kmeans(data, 2, None, criteria, 10, flags)

# K-Means聚类 聚集成4类
compactness, labels4, centers4 = cv2.kmeans(data, 4, None, criteria, 10, flags)

# K-Means聚类 聚集成8类
compactness, labels8, centers8 = cv2.kmeans(data, 8, None, criteria, 10, flags)

# K-Means聚类 聚集成16类
compactness, labels16, centers16 = cv2.kmeans(data, 16, None, criteria, 10, flags)

# K-Means聚类 聚集成64类
compactness, labels64, centers64 = cv2.kmeans(data, 64, None, criteria, 10, flags)

# 图像转换回uint8二维类型
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))

centers4 = np.uint8(centers4)
res = centers4[labels4.flatten()]
dst4 = res.reshape((img.shape))

centers8 = np.uint8(centers8)
res = centers8[labels8.flatten()]
dst8 = res.reshape((img.shape))

centers16 = np.uint8(centers16)
res = centers16[labels16.flatten()]
dst16 = res.reshape((img.shape))

centers64 = np.uint8(centers64)
res = centers64[labels64.flatten()]
dst64 = res.reshape((img.shape))

# 图像转换为RGB显示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
dst2 = cv2.cvtColor(dst2, cv2.COLOR_BGR2RGB)
dst4 = cv2.cvtColor(dst4, cv2.COLOR_BGR2RGB)
dst8 = cv2.cvtColor(dst8, cv2.COLOR_BGR2RGB)
dst16 = cv2.cvtColor(dst16, cv2.COLOR_BGR2RGB)
dst64 = cv2.cvtColor(dst64, cv2.COLOR_BGR2RGB)

# 用来正常显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']

# 显示图像
titles = [u'原始图像', u'聚类图像 K=2', u'聚类图像 K=4',
          u'聚类图像 K=8', u'聚类图像 K=16', u'聚类图像 K=64']
images = [img, dst2, dst4, dst8, dst16, dst64]
for i in range(6):
    plt.subplot(2, 3, i + 1), plt.imshow(images[i], 'gray'),
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　我们依然采用上面的图：

2，图像采样处理

2.1 图像采样处理概述

　　图像采样（Image Sampling）是将一幅连续图像在空间上分割成 M*N 个网格，每个网格用一个亮度值或灰度值来表示，其示意图如下所示：

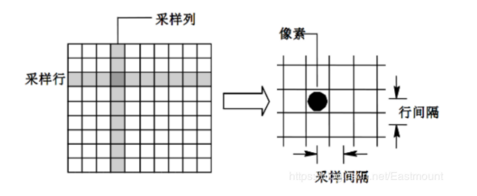
 　　图像采样的间隔越大，所得图像像素数越少，空间分辨率越低，图像质量越差，甚至出现马赛克效益；相反，图像采样的间隔越小，所得图像像素数越多，空间分辨率越高，图像质量越好，但数据量会相应的增大。

　　马赛克原理：将图像中选中区域的像素值用这个选中区域中的某一像素值或者随机值替换。

　　下图中将指定区域的像素点值，全部改为左上角第一个点的像素点值：

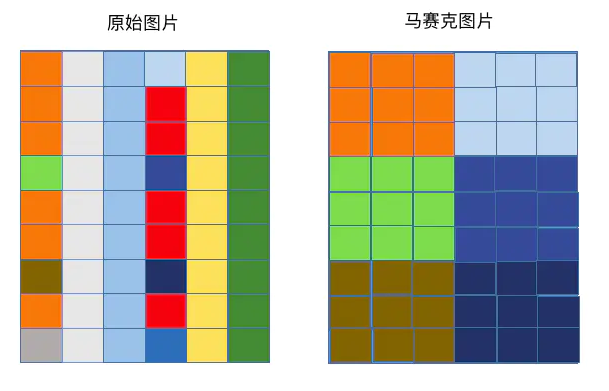
2.2  图像采样Python实现

　　下面学习Python图像采样处理相关代码操作。其核心流程是建立一张临时图片，设置需要采用的区域大小（如 16*16），接着循环遍历原始图像中所有像素点，采样区域内的像素点赋值相同（如左上角像素点的灰度值），最终实现图像采样处理。代码是进行16*16采样的过程。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('kd2.jpg')

# 获取图像的高度和宽度
height, width = img.shape[0], img.shape[1]
# print(img.shape)  # (352, 642, 3)
# 采样转换成 16*16 区域
numHeight, numWidth = height / 16, width / 16

# 创建一幅图像，内容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)

# 图像循环采样 16*16 区域
for i in range(16):
    # 获取Y坐标
    y = int(i * numHeight)
    for j in range(16):
        # 获取 X 坐标
        x = int(j * numWidth)
        # 获取填充颜色，左上角像素点
        b = img[y, x][0]
        g = img[y, x][1]
        r = img[y, x][2]

        # 循环设置小区域采样
        for n in range(int(numHeight)):
            for m in range(int(numWidth)):
                new_img1[y+n, x+m][0] = np.uint8(b)
                new_img1[y+n, x+m][1] = np.uint8(g)
                new_img1[y+n, x+m][2] = np.uint8(r)

# 显示图像
cv2.imshow('src', img)
cv2.imshow('new src', new_img1)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　结果如下：

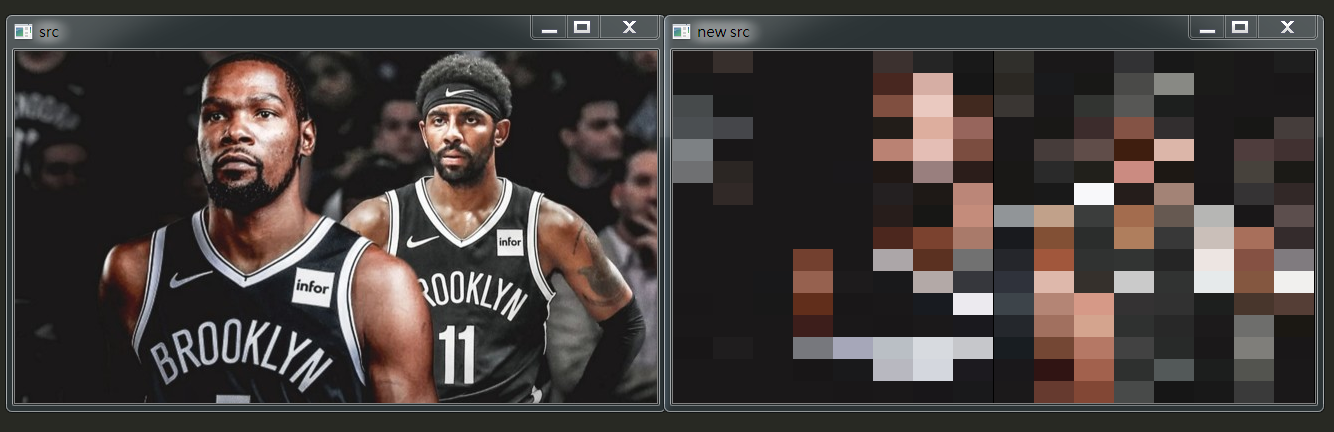
 　　同样，可以对彩色图片进行采样处理，下面的代码将彩色风景采样处理成 8*8的马赛克区域。

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('kd2.jpg')

# 获取图像的高度和宽度
height, width = img.shape[0], img.shape[1]
# print(img.shape)  # (352, 642, 3)
# 采样转换成 8*8 区域
numHeight, numWidth = height / 8, width / 8

# 创建一幅图像，内容使用零填充
new_img1 = np.zeros((height, width, 3), np.uint8)

# 图像循环采样 8*8 区域
for i in range(8):
    # 获取Y坐标
    y = int(i * numHeight)
    for j in range(8):
        # 获取 X 坐标
        x = int(j * numWidth)
        # 获取填充颜色，左上角像素点
        b = img[y, x][0]
        g = img[y, x][1]
        r = img[y, x][2]

        # 循环设置小区域采样
        for n in range(int(numHeight)):
            for m in range(int(numWidth)):
                new_img1[y+n, x+m][0] = np.uint8(b)
                new_img1[y+n, x+m][1] = np.uint8(g)
                new_img1[y+n, x+m][2] = np.uint8(r)

# 显示图像
cv2.imshow('src', img)
cv2.imshow('new src', new_img1)
# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　结果如下：

 　　但是上述代码存在一个问题，就是当图片的长度和宽度不能被采样区域整除时，输出图像的最右边和最下边的区域没有被采样处理。这里推荐大家做一个求余运算，将不能整除部分的区域也进行采样处理。

2.3   局部马赛克处理

　　前面学习了对整幅图像做了采样处理，那么如何对图像的局部区域进行马赛克处理呢？

　　实现用按下鼠标左键拖动时，在鼠标经过的路径上打上马赛克，而马赛克的原理是将图像中选中区域的像素用这个选中区域中的某一像素覆盖，为了不让鼠标重复经过图像中同一个的时候，选取不一样的像素，该程序将在输入图片的时候，就实现了全图的马赛克效果。而当鼠标划过的时候，程序只是将实现马赛克的图像的指定位置复制到显示的图像中。

　　下面代码实现了该功能，当鼠标按下时，它能够给鼠标拖动的区域打上马赛克，并按下 “s”键保存图像到本地。

 　　代码如下：

# _*_coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt


# 鼠标事件
def draw(event, x, y, flags, parma):
    global en
    # 鼠标左键按下开启 en 键
    if event == cv2.EVENT_LBUTTONDOWN:
        en = True
    # 鼠标左键按下并且移动
    elif event == cv2.EVENT_MOUSEMOVE and flags == cv2.EVENT_LBUTTONDOWN:
        # 调用函数打马赛克
        if en:
            drawMask(y, x)
        # 鼠标左键弹起结束操作
        elif event == cv2.EVENT_LBUTTONUP:
            en = False


# 图像局部采用操作
def drawMask(x, y, size=10):
    # size*size 采样处理
    m = int(x / size * size)
    n = int(y / size * size)
    # 10*10 区域设置为同一像素值
    for i in range(int(size)):
        for j in range(int(size)):
            img[m+i][n+j] = img[m][n]

if __name__ == '__main__':
    # 读取原始图像
    img = cv2.imread('durant.jpg')
    # 设置鼠标右键开启
    en = False

    # 打开对话框
    cv2.namedWindow('image')
    # 调用draw 函数设置鼠标操作
    cv2.setMouseCallback('image', draw)

    # 循环处理
    while(1):
        cv2.imshow('image', img)
        # 按 ESC键退出
        if cv2.waitKey(10) & 0xFF == 27:
            break
        # 按 s 键保存图片
        elif cv2.waitKey(10) & 0xFF == 115:
            cv2.imwrite('save.jpg', img)
    # 退出窗口
    cv2.destroyAllWindows()

　　打了马赛克的图片如下：

 　　我将他的号码打码了。

 

参考文献：https://blog.csdn.net/Eastmount/article/details/89218513

https://blog.csdn.net/Eastmount/article/details/89287543