OpenCV计算机视觉学习（11）——图像空间几何变换（图像缩放，图像旋转，图像翻转，图像平移，仿射变换，镜像变换）

如果需要处理的原图及代码，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/ComputerVisionPractice

　　图像的几何变换是在不改变图像内容的前提下对图像像素进行空间几何变换，主要包括了图像的平移变换，缩放，旋转，翻转，镜像变换等。

1，几何变换的基本概念

1.1 坐标映射关系

　　图像的几何变换改变了像素的空间位置，建立一种原图像像素与变换后图像像素之间的映射关系，通过这种映射关系能够实现下面两种计算：

• 1，原图像任意像素计算该像素在变换后图像的坐标位置
• 2，变换后图像的任意像素在原图像的坐标位置

　　对于第一种计算，只要给出原图像上的任意像素坐标，都能通过对应的映射关系获得到该像素在变换后图像的坐标位置。将这种输入图像坐标映射到输出的过程称为“向前映射”。反过来，知道任意变换后图像上的像素坐标，计算其在原图像的像素坐标，将输出图像映射到输入的过程称为“向后映射”。但是，在使用向前映射处理几何变换时却有一些不足，通常会产生两个问题：映射不完全，映射重叠。

　　1，映射不完全

　　输入图像的像素总数小于输出图像，这样输出图像中的一些像素找不到在原图像中的映射。

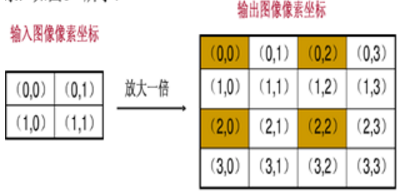
　　上图中只有四个坐标点根据映射关系在原图像找到了相对应的像素，其余12个坐标没有有效值。

　　2，映射重叠

　　根据映射关系，输入图像的多个像素映射到输出图像的同一个像素上。

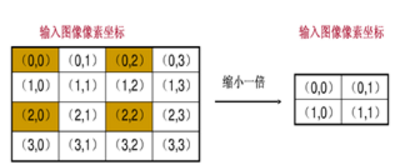
 　　上面左上角的四个像素都会映射到输出图像的（0， 0）那么我们输出的（0,0）应该取那个像素值呢？

　　要解决上述两个问题可以使用“向后映射”，使用输出图像的坐标反过来推算改坐标对应于原图像中的坐标位置。这样，输出图像的每个像素都可以通过映射关系在原图像中找到唯一对应的像素，而不会出现映射不完全和映射重叠。所以，一般使用向后映射来处理图像的几何变换。从上面也可以看出，向前映射之所以会出现问题，主要是由于图像像素的总数发生了变换，也就是图像的大小改变了。在一些图像大小不会发生变化的变换中，向前映射还是很有效的。

1.2 插值算法

　　对于数字图像而言，像素的坐标是离散型非负整数，但是在进行变换的过程中有可能产生浮点坐标值。例如，原图像坐标（9, 9）在缩小一倍时会变成（4.5,  4.5），这显然是一个无效的坐标。插值算法就是用来处理这些浮点坐标的。常见的插值算法有最邻*插值法，双线性插值法，二次立方插值法，三次立方插值法等。这里主要学*最邻*插值和双线性插值。

　　最邻*插值

　　最邻*插值法，也成为零阶插值法，最简单插值算法，当然效果也是最差的。它的思想相当简单，就是四舍五入，浮点坐标的像素值等于距离该点最*的输入图像的像素值。

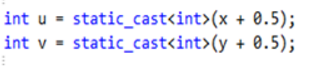
　　上面的C代码可以求得（x,  y）的最邻*插值坐标（u,  v）。

　　最邻*插值几乎没有多余的运算，速度相当快，但是这种邻*取值的方法是很粗糙的，会造成图像的马赛克，锯齿等现象。

　　双线性插值法

　　双线性插值法，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

　　双线性插值法作为数值分析的一种插值算法，广泛应用在信号处理，数字图像和视频处理等方面。

 　　下面举个简单的例子，假设要求坐标为（2.4， 3）的像素值P，该点在（2， 3）和（3， 3）之间，如下图：

　　u 和 v 分别是距离浮点坐标最*两个整数坐标像素在浮点坐标像素所占的比例。

　　P(2.4, 3) = u * P(2, 3)  +  v * P(3, 3)，混合的比例是以距离为依据的，那么u = 0.4, v = 0.6。上面是只在一条直线的插值，称为线性插值。双线性插值就是分别在x轴和Y轴上做线性插值运算。

　　已知的红色数据点与待插值得到的绿色点。

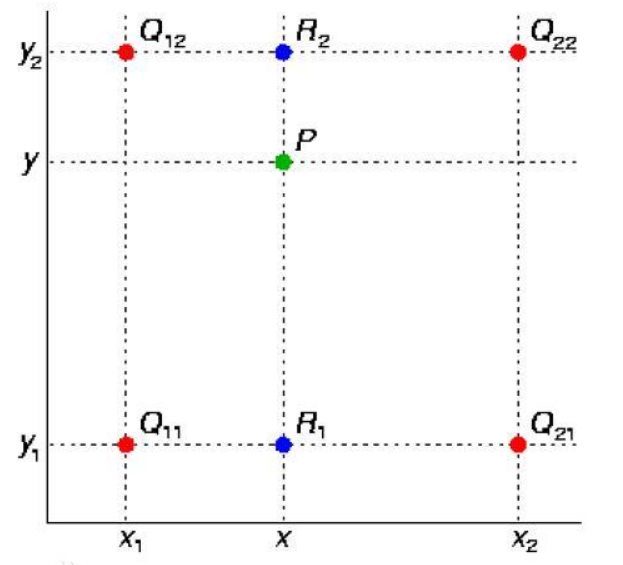
 　　假如我们想得到未知函数 f 在点 P=(x, y) 的值，假设我们已知函数f 在Q11 = （x1, y1），Q12 = (x1,y2)，Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

　　首先在x方向进行线性插值，得到R1， R2，然后在y方向进行线性插值，得到P。这样就得到所要的结果 f(x, y)

　　其中红色点Q11, Q12, Q21, Q22为已知的4个像素点。

　　第一步：X方向的线性插值，在Q12， Q22中插入蓝色点R2， Q11， Q21 中插入蓝色点R1

　　第二步：Y方向的线性插值，通过第一步计算出的R1与R2在y方向上的插值计算出P点。

　　线性插值的结果与插值的顺序无关，首先进行y方向的插值，然后进行X方向的插值，所得到的结果是一样的，双线性插值的结果与先进行哪个方向的插值无关。

　　在X方向上：

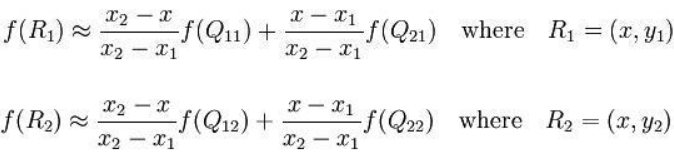
　　在y方向上：

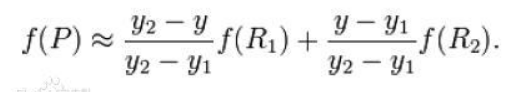
　　如果选择一个坐标系统使得四个已知的点坐标分别为（0, 0）(0, 1) (1, 0) (1, 1)，那么插值公式就可以简化为：

　　　　f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy

　　在x与y方向上，z值成单调性特性的应用中，此种方法可以做外插运算，即可以求解Q1~Q4所构成的正方形以外的点的值。

2，图像缩放

　　图像缩放主要用于改变图像的大小，缩放后图像的宽度和高度会发生变换。水平缩放系数，控制图像宽度的缩放，其值为1，则图像的宽度不变；垂直缩放系数控制图像高度的缩放，其值为1，则图像高度不变。如果水平缩放和垂直缩放系数不相等，那么缩放后图像的宽度和高度的比例会发生变换，会使图像变形。要保持图像宽度和高度的比例不发生变换，就需要水平缩放系数和垂直缩放系数相等。

2.1 图像缩放原理

　　设水平缩放系数为Sx，垂直缩放系数为Sy，（x0,   y0）为缩放前坐标，（x,  y）为缩放后坐标，其缩放的坐标映射关系为：

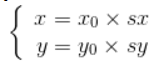
 　　矩阵表示的形式为：

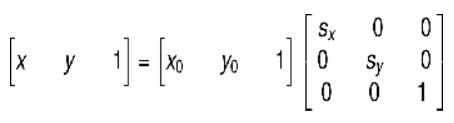
　　这是前向映射，在缩放的过程改变了图像的大小，使用前向映射会出现映射重叠和映射不完全的问题，所以这里更关系的是向后映射，也就是输出图像通过向后映射关系找到其在原图像中对应的像素。

　　向后映射关系：

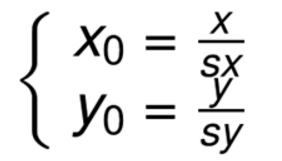
2.2 基于OpenCV的缩放实现

　　在图像缩放时，首先要计算缩放后图像的大小，设 newWidth，newHeight为缩放后的图像的宽和高，width，height为原图像的宽度和高度，那么有：

　　然后遍历缩放后的图像，根据向后映射关系计算出缩放的像素在原图像中像素的位置，如果得到的浮点坐标，就需要使用插值算法取得*似的像素值。

　　图像缩放主要调用 resize() 函数实现，具体如下：

def resize(src, dsize, dst=None, fx=None, fy=None, interpolation=None)

　　其中对应的各个参数意思：

　　src：输入，原图像，即待改变大小的图像；

　　dsize：输出图像的大小。如果这个参数不为0，那么就代表将原图像缩放到这个Size(width，height)指定的大小；如果这个参数为0，那么原图像缩放之后的大小就要通过下面的公式来计算：

　　　　　　　　　　　　　　dsize = Size(round(fx*src.cols), round(fy*src.rows))

其中，fx和fy就是下面要说的两个参数，是图像width方向和height方向的缩放比例。

　　fx：width方向的缩放比例，如果它是0，那么它就会按照(double)dsize.width/src.cols来计算；

　　fy：height方向的缩放比例，如果它是0，那么它就会按照(double)dsize.height/src.rows来计算；

　　interpolation：这个是指定插值的方式，图像缩放之后，肯定像素要进行重新计算的，就靠这个参数来指定重新计算像素的方式，有以下几种：

• INTER_NEAREST                 - 最邻*插值
• INTER_LINEAR                     - 双线性插值，如果最后一个参数你不指定，默认使用这种方法
• INTER_AREA                         -  使用像素区域关系进行重采样    resampling using pixel area relation. It may be a preferred method for image decimation, as it gives moire’-free results. But when the image is zoomed, it is similar to the INTER_NEAREST method.
• INTER_CUBIC                      - 4x4像素邻域内的双立方插值
• INTER_LANCZOS4             - 8x8像素邻域内的Lanczos插值

　　对于插值方法，正常情况下使用默认的双线性插值法就够了。几种常用方法的效率为：

最邻*插值>双线性插值>双立方插值>Lanczos插值

　　但是效率和效果是反比的，所以根据自己的情况酌情使用。

　　注意：输出的尺寸格式为（宽，高）

　　dsize与 fx和fy 两个设置一个即可实现图像缩放，例如：

1. result = cv2.resize(src, (160,160))
2. result = cv2.resize(src, None, fx=0.5, fy=0.5)

　　图像缩放：设（x0, y0）是缩放后的坐标，（x,  y）是缩放前的坐标，sx, sy为缩放因子，则公式如下：

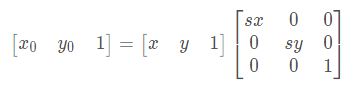
 　　代码1如下（dsize中第一个是列数  第二个是函数）：

# encoding:utf-8
import cv2
import numpy as np

# 读取图片
src = cv2.imread('test.jpg')

# 图像缩放
result = cv2.resize(src, (200, 100))
print(result.shape)

# 显示图像
cv2.imshow("src", src)
cv2.imshow("result", result)

# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　代码2如下：（获取原始图像像素再乘以缩放系数进行图像变换）

#encoding:utf-8
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('test.jpg')
rows, cols = src.shape[:2]
print rows, cols

#图像缩放 dsize(列,行)
result = cv2.resize(src, (int(cols*0.6), int(rows*1.2)))

#显示图像
cv2.imshow("src", src)
cv2.imshow("result", result)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　代码3如下：（（fx , fy）缩放倍数的方法对图像进行放大或缩小）

#encoding:utf-8
import cv2  
import numpy as np  
 
#读取图片
src = cv2.imread('test.jpg')
rows, cols = src.shape[:2]
print rows, cols

#图像缩放
result = cv2.resize(src, None, fx=0.3, fy=0.3)

#显示图像
cv2.imshow("src", src)
cv2.imshow("result", result)

#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　

3，图像旋转

3.1 图像旋转的原理

　　图像的旋转就是让图像按照某一点旋转指定的角度。图像旋转后不会变形，但是其垂直对称轴和水平对称轴都会发生改变，旋转后的图像的坐标和原图像坐标之间的关系已不能通过简单的加减乘法得到，而需要通过一系列的复杂运算。而且图像在旋转后其宽度和高度都会发生变换，其坐标原点会发生变换。

　　图像所用的坐标系不是常用的笛卡尔，其左上角是其坐标原点，X轴沿着水平方向向右，Y轴沿着竖直方向向下。而在旋转的过程一般使用旋转中心未坐标原点的笛卡尔坐标系，所以图像旋转的第一步就是坐标系的变换。设旋转中心未（x0,  y0），（x',  y'）是旋转后的坐标，（x,  y）是旋转后的坐标，则坐标变换如下：

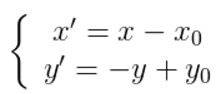
　　矩阵表示为：

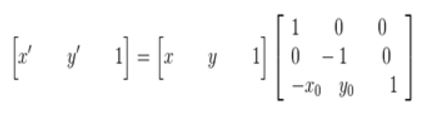
　　在最终的实现中，常用到的是有缩放后的图像通过映射关系找到其坐标在原图像中的相应位置，这就需要上述映射的逆变换：

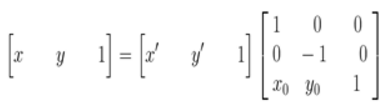
　　坐标系变换到以旋转中心为原点后，接下来就要对图像的坐标进行变换。

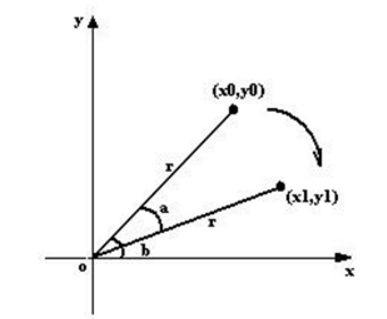
　　上图所示，将坐标（x0,  y0）顺时针方向旋转 a，得到（x1,  y1）。旋转前有：

　　旋转a后有：

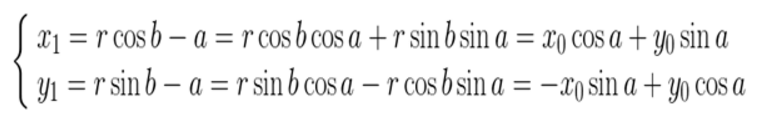
　　矩阵的表示形式：

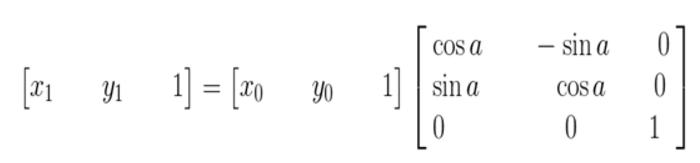　　其逆变换：

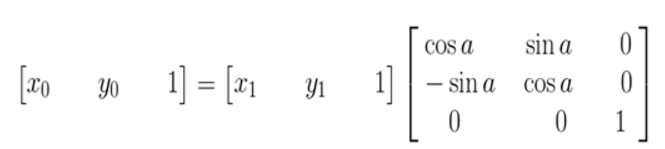
 　　由于在旋转的时候是以旋转中心未坐标原点的，旋转结束后还需要将坐标原点移到图像左上角，也就是还要进行一次变换。这里需要注意的是，旋转中心的坐标（x0,  y0）是在以原图像的左上角为坐标原点的坐标系中得到，而在旋转后由于图像的宽和高发生了变换，也就导致了旋转后图像的坐标原点和旋转前的发生了变换。

　　上面两图可以清晰的看到，旋转前后图像的左上角，也就是坐标原点发生了变换。

　　在求图像旋转后左上角的坐标前，先来看看旋转后图像的宽和高。从上图可以看出，旋转后图像的宽和高与原图像的四个角旋转后的位置有关。

　　设top为旋转后最高点的纵坐标，down为旋转后最低点的纵坐标，left为旋转后最左边点的横坐标，right为旋转后最右边点的横坐标。

　　旋转后的宽和高为 newWidth，newHeight，则可以得到下面的关系：

　　也就很容易的得出旋转后图像左上角坐标（left，top）（以旋转中心为原点的坐标系），故在旋转完成后要将坐标系转换为以图像的左上角为坐标原点，可由下面变换关系得到：

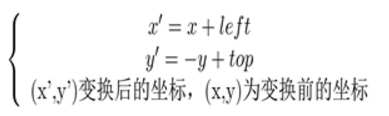
　　矩阵表示：

　　其逆变换：

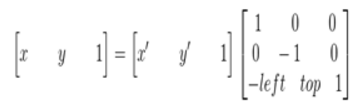　　综合以上，也就是说原图像的像素坐标要经过三次的坐标变换：

• 1，将坐标原点由图像的左上角变换到旋转中心
• 2，以旋转中心为原点，图像旋转角度a
• 3，旋转结束后，将坐标原点变换到旋转后图像的左上角

 　　可以得到下面的旋转公式：（x',  y'）旋转后的坐标，（x,  y）原坐标，（x0,  y0）旋转中心，a旋转的角度（顺时针）

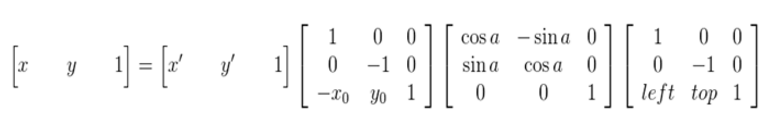
　　这种由输入图像通过映射得到输出图像的坐标，是向前映射。常用的向后映射是其逆运算

 

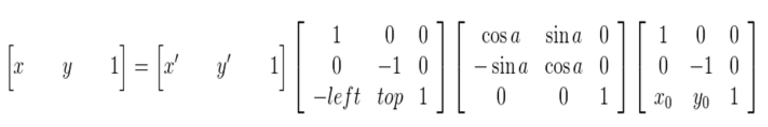
3.2 基于OpenCV实现图像旋转

　　图像旋转主要调用 getRotationMatrix2D() 函数和 wrapAffine() 函数实现，绕图像的中心旋转，具体如下：

M = cv2.getRotationMatrix2D((cols/2, rows/2), 30, 1)
参数分别为：旋转中心、旋转度数、scale

rotated = cv2.warpAffine(src, M, (cols, rows))
参数分别为：原始图像、旋转参数、原始图像宽高

　　图像旋转：设（x0,  y0）是旋转后的坐标，（x,  y）是旋转前的坐标，（m  ,n）是旋转中心，a是旋转的角度，（left,  top）是旋转后图像的左上角坐标，则公式如下：

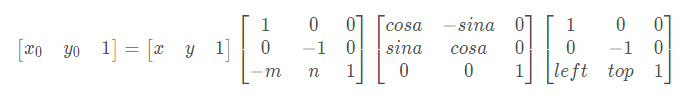
 　　代码如下：

# encoding:utf-8
import cv2
import numpy as np

# 读取图片
src = cv2.imread('test.jpg')

# 原图的高、宽 以及通道数
rows, cols, channel = src.shape

# 绕图像的中心旋转
# 参数：旋转中心 旋转度数 scale
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 30, 1)
# 参数：原始图像 旋转参数 元素图像宽高
rotated = cv2.warpAffine(src, M, (cols, rows))

res = np.column_stack((src, rotated))

# 显示图像
cv2.imshow("src  roteted", res)
# cv2.imshow("src", src)
# cv2.imshow("rotated", rotated)

# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　效果如下：

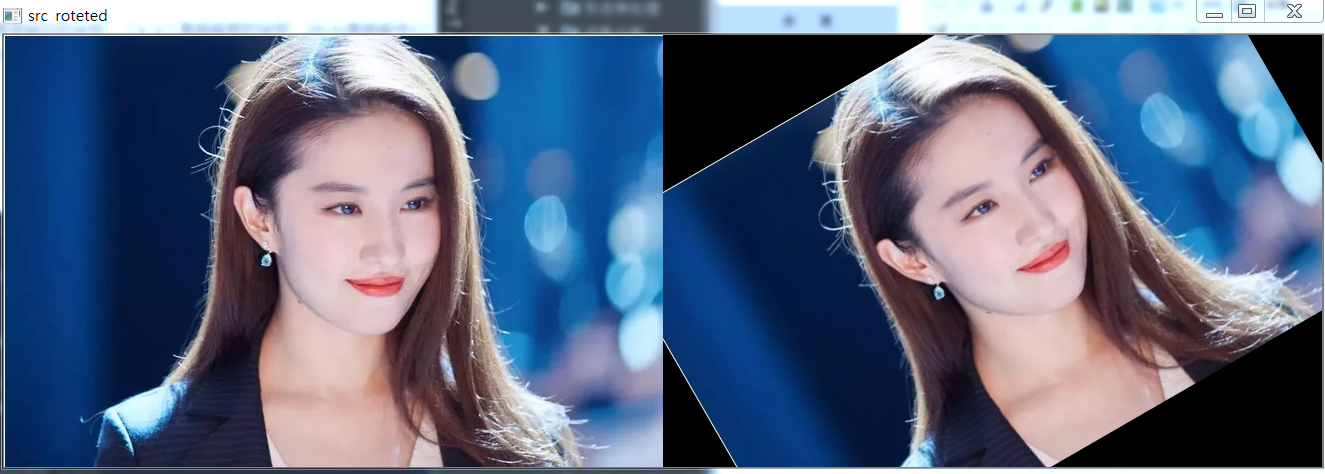
 　　如果设置 -90度，则核心代码如下：

M = cv2.getRotationMatrix2D((cols/2, rows/2), -90, 1)

rotated = cv2.warpAffine(src, M, (cols, rows))

4，图像翻转

　　图像翻转在OpenCV中调用函数 flip() 实现，原型如下：

dst = cv2.flip(src, flipCode)

　　其中 src表示原始图像，flipCode表示翻转方向（如果flipCode为0，则以X轴为对称轴翻转，如果flipCode>0，则以Y轴为对称轴翻转，如果flipCode<0，则在X轴，Y轴方向同时翻转）

　　代码如下：

#encoding:utf-8
import cv2  
import numpy as np
import matplotlib.pyplot as plt
 
#读取图片
img = cv2.imread('test.jpg')
src = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)

#图像翻转
#0以X轴为对称轴翻转 >0以Y轴为对称轴翻转 <0X轴Y轴翻转
img1 = cv2.flip(src, 0)
img2 = cv2.flip(src, 1)
img3 = cv2.flip(src, -1)

#显示图形
titles = ['Source', 'Image1', 'Image2', 'Image3']  
images = [src, img1, img2, img3]  
for i in range(4):  
   plt.subplot(2,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()  

　　效果如下：

 

5，图像平移

　　图像的平移变换就是将图像所有的像素坐标分别加上指定的水平偏移量和垂直偏移量。

5.1 平移变换原理

　　设 dx 为水平偏移量，dy为垂直偏移量，（x0,  y0）为原图像坐标，（x,  y）为变换后图像坐标，则平移变换的坐标映射为：

　　这是前向映射，即将原图像的坐标映射到变换后的图像上。其逆变换为：

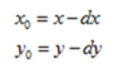
　　这是向后映射，即将变换后的图像坐标映射到原图像上。

　　在图像的几何变换中，一般使用向后映射。

5.2 基于OpenCV实现

　　图像平移：设（x0，y0）是平移后的坐标，（x, y）是平移前的坐标，dx，dy 为偏移量，则公式如下：

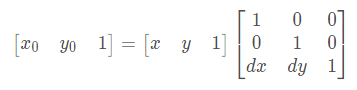
 　　图像平移首先定义平移矩阵M，再调用 warpAffine() 函数实现平移，核心函数如下：

M = np.float32([[1, 0, x], [0, 1, y]])

shifted = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

　　完整代码如下：

# encoding:utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('test.jpg')
image = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 图像平移 下、上、右、左平移
M = np.float32([[1, 0, 0], [0, 1, 100]])
img1 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, 0], [0, 1, -100]])
img2 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, 100], [0, 1, 0]])
img3 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, -100], [0, 1, 0]])
img4 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

# 显示图形
titles = ['Image1', 'Image2', 'Image3', 'Image4']
images = [img1, img2, img3, img4]
for i in range(4):
    plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　效果如下：

 

6，图像仿射变换

　　图像仿射变换又称为图像仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。通常图像的旋转加上拉伸就是图像的仿射变换，仿射变换需要一个 M 矩阵实现，但是由于仿射变换比较复杂，很难找到这个 M 矩阵。

　　OpenCV提供了根据变换前后三个点的对应关系来自动求解 M 的函数——cv2.getAffineTransform( pos1,  pos2)，其中 pos1和 pos2 表示变换前后的对应位置关系，输出的结果为仿射矩阵M，接着使用函数 cv2.warpAffine() 实现图像仿射变换，下图是仿射变换的前后效果图。

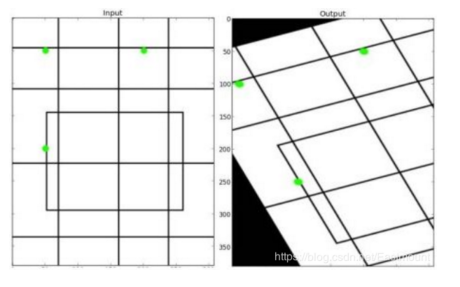
　　图像仿射变换的函数原型如下：

M = cv2.getAffineTransform(pos1,pos2)

 　　参数含义：

• pos1表示变换前的位置
• pos2表示变换后的位置

cv2.warpAffine(src, M, (cols, rows))

 　　参数含义：

• src表示原始图像
• M表示仿射变换矩阵
• (rows,cols)表示变换后的图像大小，rows表示行数，cols表示列数

　　实现的代码如下：

# _*_ coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('liu.jpg')

# 获取图片大小
rows, cols = img.shape[:2]

# 设置图像仿射变换矩阵
pos1 = np.float32([[50, 50], [200, 50], [50, 200]])
pos2 = np.float32([[10, 100], [200, 50], [100, 250]])
M = cv2.getAffineTransform(pos1, pos2)

# 图像仿射变换
result = cv2.warpAffine(img, M, (cols, rows))

# 显示图像
cv2.imshow('origin', img)
cv2.imshow('result', result)

# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

 　　结果如下：

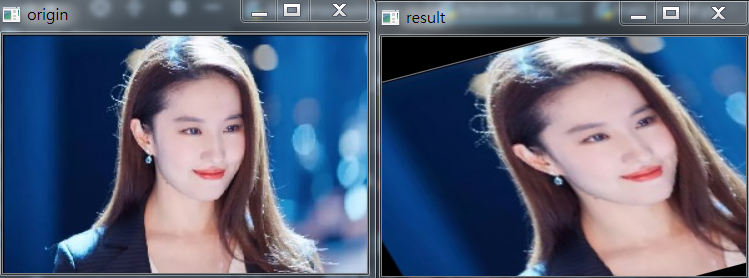
 　　仿射变换允许图像倾斜并且可以在任意两个方向上发生伸缩，代码如下：

def random_warp(img, row, col):
    height, width, channels = img.shape
 
    random_margin = 100
    x1 = random.randint(-random_margin, random_margin)
    y1 = random.randint(-random_margin, random_margin)
    x2 = random.randint(width - random_margin - 1, width - 1)
    y2 = random.randint(-random_margin, random_margin)
    x3 = random.randint(width - random_margin - 1, width - 1)
    y3 = random.randint(height - random_margin - 1, height - 1)
    x4 = random.randint(-random_margin, random_margin)
    y4 = random.randint(height - random_margin - 1, height - 1)
 
    dx1 = random.randint(-random_margin, random_margin)
    dy1 = random.randint(-random_margin, random_margin)
    dx2 = random.randint(width - random_margin - 1, width - 1)
    dy2 = random.randint(-random_margin, random_margin)
    dx3 = random.randint(width - random_margin - 1, width - 1)
    dy3 = random.randint(height - random_margin - 1, height - 1)
    dx4 = random.randint(-random_margin, random_margin)
    dy4 = random.randint(height - random_margin - 1, height - 1)
 
    pts1 = np.float32([[x1, y1], [x2, y2], [x3, y3], [x4, y4]])
    pts2 = np.float32([[dx1, dy1], [dx2, dy2], [dx3, dy3], [dx4, dy4]])
     
     
    M_warp = cv2.getPerspectiveTransform(pts1, pts2)
    img_warp = cv2.warpPerspective(img, M_warp, (width, height))
    return img_warp
 
img_warp = random_warp(img, img.shape[0], img.shape[1])
 
cv2.imshow('img_warp', img_warp)
key = cv2.waitKey(0)
if key == 27:
    cv2.destroyAllWindows()

 

7，图像的镜像变换

　　图像的镜像变换分为两种：水平镜像和垂直镜像。水平镜像以图像垂直中线为轴，将图像的像素进行对换，也就是将图像的左半部和右半部对调。垂直镜像则是以图像的水平中线为轴，将图像的上半部分和下半部分对调，效果如下：

7.1  镜像变换原理

　　设图像的宽度为 width，长度为 height。（x,  y）为变换后的坐标，（x0,  y0）为原图像的坐标。

　　1，水平镜像变换的向前映射为：

　　向后映射，即水平镜像变换向前变换的逆变换，为：

　　2，垂直镜像变换的前向映射为：

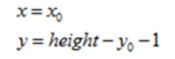
　　向后映射，即垂直镜像变换的前向变换的逆变换，为：

 

8，图像透视变换

　　图像透视变换（Perspective Transformation）的本质是将图像投影到一个新的视平面，同理OpenCV通过函数 cv2.getPerspectiveTransform(pos1, pos2)构造矩阵M，其中pos1和pos2分别表示变换前后的四个点对应的位置。得到M后在通过函数 cv2.warpPerspective(src, M, (cols, rows)) 进行透视变换。

　　图像透视变换的函数原型如下：

M = cv2.getPerspectiveTransform(pos1, pos2)

 　　参数意义：

• pos1表示透视变换前的4个点对应位置
• pos2表示透视变换后的4个点对应位置

cv2.warpPerspective(src,M,(cols,rows))

 　　参数意义：

• src表示原始图像
• M表示透视变换矩阵
• (rows,cols)表示变换后的图像大小，rows表示行数，cols表示列数

　　代码如下：

# _*_ coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('liu.jpg')

# 获取图片大小
rows, cols = img.shape[:2]

# 设置图像透视变换矩阵
pos1 = np.float32([[114, 82], [287, 156], [8, 322], [216, 333]])
pos2 = np.float32([[0, 0], [188, 0], [0, 262], [188, 262]])
M = cv2.getPerspectiveTransform(pos1, pos2)

# 图像透视变换
result = cv2.warpPerspective(img, M, (cols, rows))

# 显示图像
cv2.imshow('origin', img)
cv2.imshow('result', result)

# 等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()

　　结果如下：

8.1  将旋转的图片还原

　　这里不理解的可以学*一下我下面这篇博客：

深入学*OpenCV文档扫描OCR识别及答题卡识别判卷（文档扫描，图像矫正，透视变换，OCR识别）

　　这里画一个简易图，简单来看如下：

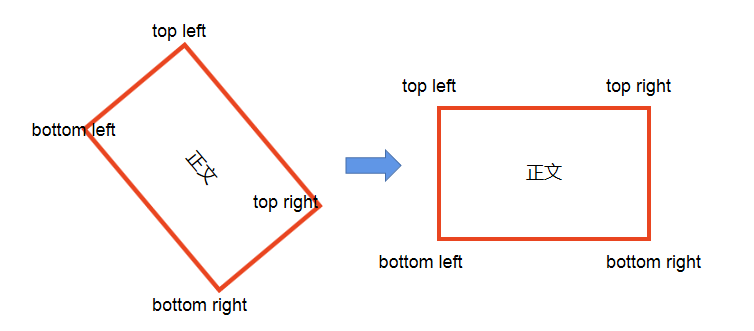
 　　当找到需要旋转的四个坐标点之后，如上图所示，分别为左上，右上，右下，左下四个点。找到这四个点之后，我们对其进行旋转还原。部分代码如下：

　　注意：这里我画的是矩形，但是实际上可能会出现不规则四边形。

def order_points(pts):
    # 一共四个坐标点
    rect = np.zeros((4, 2), dtype='float32')
    
    # 按顺序找到对应的坐标0123 分别是左上，右上，右下，左下
    # 计算左上，由下
    # numpy.argmax(array, axis) 用于返回一个numpy数组中最大值的索引值
    s = pts.sum(axis=1)  
    print(s)
    rect[0] = pts[np.argmin(s)]
    rect[2] = pts[np.argmax(s)]

    # 计算右上和左
    # np.diff()  沿着指定轴计算第N维的离散差值  后者-前者
    diff = np.diff(pts, axis=1)
    rect[1] = pts[np.argmin(diff)]
    rect[3] = pts[np.argmax(diff)]
    return rect


# 透视变换
def four_point_transform(image, pts):
    # 获取输入坐标点
    print('origin:',pts)
    rect = order_points(pts)
    print('finally:',rect)
    (tl, tr, br, bl) = rect

    # 计算输入的w和h的值
    widthA = np.sqrt(((br[0] - bl[0])**2) + ((br[1] - bl[1])**2))
    widthB = np.sqrt(((tr[0] - tl[0])**2) + ((tr[1] - tl[1])**2))
    maxWidth = max(int(widthA), int(widthB))

    heightA = np.sqrt(((tr[0] - br[0])**2) + ((tr[1] - br[1])**2))
    heightB = np.sqrt(((tl[0] - bl[0])**2) + ((tl[1] - bl[1])**2))
    maxHeight = max(int(heightA), int(heightB))

    # 变化后对应坐标位置
    dst = np.array([
        [0, 0],
        [maxWidth - 1, 0],
        [maxWidth - 1, maxHeight - 1],
        [0, maxHeight - 1]],
        dtype='float32')    

    # 计算变换矩阵
    M = cv2.getPerspectiveTransform(rect, dst)
    warped = cv2.warpPerspective(image, M, (maxWidth, maxHeight))

    # 返回变换后的结果
    return warped

 

8.1 基于图像透视变换的图像矫正

　　也可以直接参考我下面博客进行实战：

深入学*OpenCV文档扫描OCR识别及答题卡识别判卷（文档扫描，图像矫正，透视变换，OCR识别）

　　此例子参考：https://blog.csdn.net/t6_17/article/details/78729097

　　实现内容：图像矫正，下图是一张图像中有A4纸，通过图像处理的方法将其矫正。

　　输入图像：

 　　处理代码：

# _*_ coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('paper.jpg')

# 获取图像大小
rows, cols = img.shape[:2]

# 将原图像高斯模糊
img = cv2.GaussianBlur(img, (3, 3), 0)
# 然后进行灰度化处理
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 边缘检测（检测出图像的边缘信息)
edge = cv2.Canny(gray, 50, 250, apertureSize=3)
# cv2.imshow('canny', edge)
#
# cv2.waitKey(0)
# cv2.destroyAllWindows()

# 通过霍夫变换得到A4纸边缘
# 可以看到A4纸外还有一些线，可以通过霍夫变换去掉这些先
lines = cv2.HoughLinesP(edge, 1, np.pi/180, 100, minLineLength=90, maxLineGap=10)
# 下面输出的四个点分别为四个顶点
for x1, y1, x2, y2 in lines[0]:
    print((x1, y1), (x2, y2))
for x1, y1, x2, y2 in lines[1]:
    print((x1, y1), (x2, y2))
# (9, 564) (140, 254)
# (355, 636) (421, 464)

# 绘制边缘
for x1, y1, x2, y2 in lines[0]:
    cv2.line(gray, (x1, y1), (x2, y2), (0, 255, 0), 2)
# cv2.imshow('hough', gray)
#
# cv2.waitKey(0)
# cv2.destroyAllWindows()

# 根据四个顶点设置图像透视变换矩阵
pos1 = np.float32([[140, 254], [421, 464], [9, 564], [355, 636]])
pos2 = np.float32([[0, 0], [170, 0], [0, 250], [170, 250]])
M = cv2.getPerspectiveTransform(pos1, pos2)

# 图像透视变换
result = cv2.warpPerspective(img, M, (170, 250))
cv2.imshow('result', result)

cv2.waitKey(0)
cv2.destroyAllWindows()

　　Canny处理的结果：

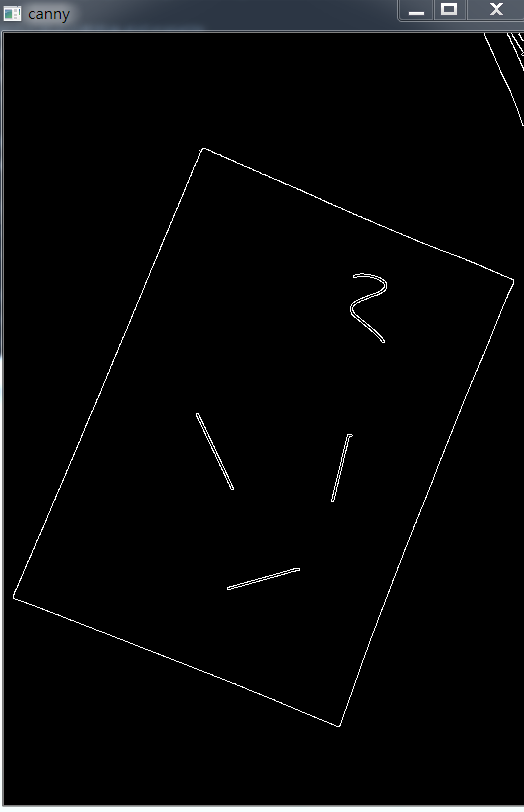
　　hough变换后的结果：

 　　我最终得到的结果：

　　效果不好， 原因大概是在网上拿到的图片是截图别人博客的图片，而且不是原像素，边界不明显，所以处理之后会存在问题。如果需要看透视变换好的例子，我上面有博客地址。

　　我的代码：

# _*_ coding:utf-8_*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('paper.jpg')
print(img.shape)  # paper1  (511, 297, 3)  paper  (772, 520, 3)

# 获取图像大小
rows, cols = img.shape[:2]

# 将原图像高斯模糊
img = cv2.GaussianBlur(img, (3, 3), 0)
# 然后进行灰度化处理
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 边缘检测（检测出图像的边缘信息)
# threshold1 表示第一个滞后性阈值 threshold2表示第二个滞后性阈值
# apertureSize 表示应用Sobel算子的孔径大小，其默认值为3
edge = cv2.Canny(gray, 50, 200, apertureSize=3)
# cv2.imshow('canny', edge)
#
# cv2.waitKey(0)
# cv2.destroyAllWindows()



# 通过霍夫变换得到A4纸边缘
# 可以看到A4纸外还有一些线，可以通过霍夫变换去掉这些先
lines = cv2.HoughLinesP(edge, 1, np.pi/180, 30, minLineLength=60, maxLineGap=10)
# 下面输出的四个点分别为四个顶点
for x1, y1, x2, y2 in lines[0]:
    print((x1, y1), (x2, y2))
for x1, y1, x2, y2 in lines[1]:
    print((x1, y1), (x2, y2))
# (9, 564) (140, 254)
# (355, 636) (421, 464)x

# 绘制边缘
for x1, y1, x2, y2 in lines[0]:
    cv2.line(gray, (x1, y1), (x2, y2), (0, 0, 255), 2)

# lines = cv2.HoughLines(edge, 1, np.pi/180, 150)
# # 提取为二维
# lines1 = lines[:, 0, :]
# for rho, theta in lines1[:]:
#     a, b = np.cos(theta), np.sin(theta)
#     x0, y0 = a*rho, b*rho
#     x1, y1 = int(x0 + 1000*(-b)), int(y0 + 1000*(a))
#     x2, y2 = int(x0 - 1000*(-b)), int(y0 - 1000*(a))
#     print(x1, x2, y1, y2)
#     cv2.line(gray, (x1, y1), (x2, y2), (0, 0, 255), 2)


# cv2.imshow('hough', gray)
#
# cv2.waitKey(0)
# cv2.destroyAllWindows()


# 根据四个顶点设置图像透视变换矩阵
pos1 = np.float32([[168, 187], [509, 246], [9, 563], [399, 519]])
pos2 = np.float32([[0, 0], [170, 0], [0, 220], [170, 220]])
M = cv2.getPerspectiveTransform(pos1, pos2)

# 图像透视变换
result = cv2.warpPerspective(img, M, (170, 250))
cv2.imshow('result', result)

cv2.waitKey(0)
cv2.destroyAllWindows()

 

9，图像几何变换总结

　　最后补充图像几何变换所有代码，完整代码如下：

# encoding:utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图片
img = cv2.imread('liu.jpg')
image = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 图像平移矩阵
M = np.float32([[1, 0, 80], [0, 1, 30]])
rows, cols = image.shape[:2]
img1 = cv2.warpAffine(image, M, (cols, rows))

# 图像缩小
img2 = cv2.resize(image, (200, 100))

# 图像放大
img3 = cv2.resize(image, None, fx=1.1, fy=1.1)

# 绕图像的中心旋转
# 源图像的高、宽 以及通道数
rows, cols, channel = image.shape
# 函数参数：旋转中心 旋转度数 scale
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 30, 1)
# 函数参数：原始图像 旋转参数 元素图像宽高
img4 = cv2.warpAffine(image, M, (cols, rows))

# 图像翻转
img5 = cv2.flip(image, 0)  # 参数=0以X轴为对称轴翻转
img6 = cv2.flip(image, 1)  # 参数>0以Y轴为对称轴翻转

# 图像的仿射
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])
pts2 = np.float32([[10, 100], [200, 50], [100, 250]])
M = cv2.getAffineTransform(pts1, pts2)
img7 = cv2.warpAffine(image, M, (rows, cols))

# 图像的透射
pts1 = np.float32([[56, 65], [238, 52], [28, 237], [239, 240]])
pts2 = np.float32([[0, 0], [200, 0], [0, 200], [200, 200]])
M = cv2.getPerspectiveTransform(pts1, pts2)
img8 = cv2.warpPerspective(image, M, (200, 200))

# 循环显示图形
titles = ['source', 'shift', 'reduction', 'enlarge', 'rotation', 'flipX', 'flipY', 'affine', 'transmission']
images = [image, img1, img2, img3, img4, img5, img6, img7, img8]
for i in range(9):
    plt.subplot(3, 3, i + 1), plt.imshow(images[i], 'gray')
    plt.title(titles[i])
    plt.xticks([]), plt.yticks([])
plt.show()

　　结果如下：

 

参考文献：https://blog.csdn.net/Eastmount/article/details/82454335

https://blog.csdn.net/Eastmount/article/details/88679772

https://www.cnblogs.com/wangguchangqing/p/4039095.html

https://www.cnblogs.com/wangguchangqing/p/4045150.html

二值化参考文献： https://blog.csdn.net/whl970831/article/details/99706730

https://blog.csdn.net/t6_17/article/details/78729097