深度学习笔记——常用的激活（激励）函数

　　激活函数（又叫激励函数，后面就全部统称为激活函数）是模型整个结构中的非线性扭曲力，神经网络的每层都会有一个激活函数。那他到底是什么，有什么作用？都有哪些常见的激活函数呢？

　　深度学习的基本原理就是基于人工神经网络，信号从一个神经元进入，经过非线性的 activation function，传入到下一层神经元；再经过该层神经元的 activate，继续往下传递，如此循环往复，直到输出层。正是由于这些非线性函数的反复叠加，才使得神经网络有足够的 capacity来抓取复杂的pattern，在各个领域取得 state-of-the-art 的结果。显而易见，activate function 在深度学习举足轻重，也是很活跃的研究领域之一。所以下面学习一下深度学习中常用的激励函数。

1，什么是激活函数？

　　神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性直接传递到下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。

2，为什么要用激活函数（激活函数的用途）？

　　简单来说：1，加入非线性因素 2，充分组合特征

　　在神经网络中，如果不对上一层结点的输出做非线性转换的话（其实相当于激活函数为 f(x)=x），再深的网络也是线性模型，只能把输入线性组合再输出，不能学习到复杂的映射关系，而这种情况就是最原始的感知机（perceptron），那么网络的逼近能力就相当有限，因此需要使用激活函数这个非线性函数做转换，这样深层神经网络表达能力就更加强大了（不再是输入的线性组合，而是几乎可以逼近任意函数）。

　　我们知道深度学习的理论基础是神经网络，在单层神经网络中（感知机 Perceptron），输入和输出计算关系如下：

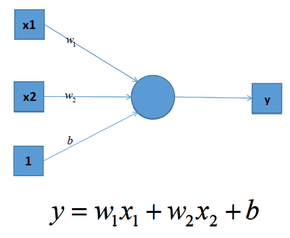
　　可见，输入与输出是一个线性关系，对于增加了多个神经元之后，计算公式也是类似，如下图：

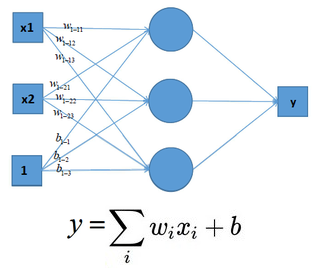
　　这样的模型就只能处理一些简单的线性数据，而对于非线性数据则很难有效的处理（也可通过组合多个不同线性表示，但这样更加复杂和不灵活），如下图所示：

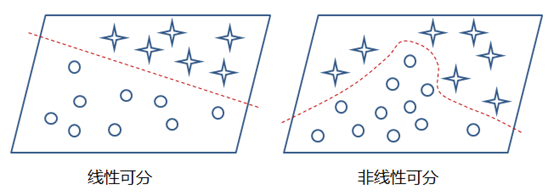
　　那么，通过在神经网络中加入非线性激励函数后，神经网络就有可能学习到平滑的曲线来实现对非线性数据的处理了，如下图所示：

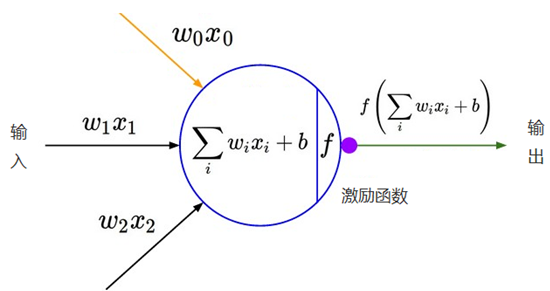
　　因此，神经网络中激励函数的作用通俗上讲就是将多个线性输入转换为非线性的关系。如果不使用激励函数的话，神经网络的每层都只是做线性变换，即使是多层输入叠加后也还是线性变换。通过激励函数引入非线性因素后，使神经网络的表达能力更强了。

3，有哪些激活函数，都有什么性质和特点？

　　早期研究神经网络主要采用Sigmoid函数或者 tanh函数，输入有界，很容易充当下一层的输入。近些年ReLU函数及其改进型（如Leaky-ReLU，P-ReLU，R-ReLU等）在多层神经网络中应用比较多。下面学习几个常用的激励函数。

3.1 激活函数的性质

非线性

　　当激活函数是线性的时候，一个层的神经网络就可以逼近基本上所有的函数了。但是，如果激活函数是恒定激活函数的时候（即 f(x)=x），就不满足这个性质了，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的，当激活函数是非线性的时候，让模型表现能力更强。

　　线性关系：两个变量之间存在一次方函数关系，就称他们之间存在线性关系。正比例是线性关系中的特例，反比例关系不是线性关系。更通俗一点讲，如果把这两个变量分别作为点的横坐标与纵坐标，其图像是平面上的一条直线，则这两个变量之间的关系就是线性关系。即如果可以用一个二元一次方程来表达两个变量之间的关系的话，这两个变量之间的关系称为线性关系，因而，二元一次方程也称为线性方程。推而广之，含有n个变量的一次方程，也称为n元线性方程，不过这已经与直线没有什么关系了。

可微性

　　当优化方法是基于梯度的时候，这个性质是必须的。

单调性

　　当激活函数是单调的时候，单层网络能够保证是凸函数

f(x) $f (x) \approx x$ x

　　当激活函数满足这个性质的时候，如果参数的初始化是 random的很小的值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要很用心的去设置初始值

输出值的范围

　　当激活函数的输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况下，一般需要更小的 learning rate。

　　基于上面性质，也正是我们使用激活函数的原因。

3.2 Sigmoid 函数

　　Sigmoid函数时使用范围最广的一类非线性激活函数，具有指数函数的形状，它在物理意义上最为接近生物神经元。其自身的缺陷，最明显的就是饱和性。从函数图可以看到，其两侧导数逐渐趋近于0，杀死梯度。

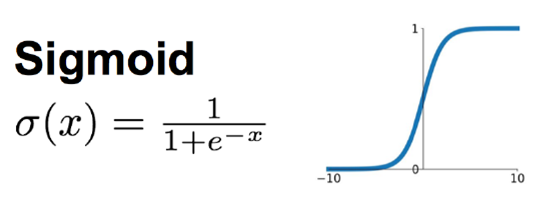
　　Sigmoid激活函数和导函数如下：

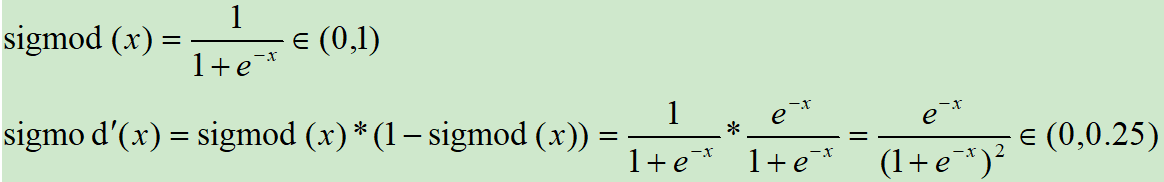
　　对应的图像如下：

　　画图对应的代码如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,1/(1+np.exp(-x)))
plt.title("y = 1/(1+exp(-x))")
plt.show()

plt.plot(x,np.exp(-x)/(1+np.exp(-x))**2)
plt.title("y = exp(-x)/(1+exp(-x))^2")
plt.show()

优点：

　　这应该是神经网络中使用最频繁的激励函数了，它把一个实数（输入的连续实值）压缩到0到1之间，当输入的数字非常大的时候，结果会接近1，当输入非常大的负数时，则会得到接近0的结果。在早期的神经网络中使用地非常多，因为它很好地解释了神经元受到刺激后是否被激活和向后传递的场景（0：几乎没有被激活；1：完全被激活）。

缺点：

　　不过近几年在深度学习的应用中比较少见到它的身影，因为使用Sigmoid函数容易出现梯度弥散或者梯度饱和。当神经网络的层数很多时，如果每一层的激活函数都采用Sigmoid函数的话，就会产生梯度弥散和梯度爆炸的问题，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

　　上面也画出了Sigmoid函数的导数图，我们可以看到，如果我们初始化神经网络的权重为[0, 1] 之间的随机数值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减少为原来的 0.25 倍，因为利用反向传播更新参数时，会乘以它的导数，所以会一直减少。如果输入的是比较大或比较小的数（例如输入100，经Sigmoid 函数后结果接近于1，梯度接近于0），会产生梯度消失现象（饱和效应），导致神经元类似于死亡状态。而当网络权值初始化为（1 , +∞）区间的值，则会出现梯度爆炸情况。

　　还有Sigmoid函数的output不是0均值（zero-centered），这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非 0 均值的信号作为输入。产生一个结果就是：如 x > 0 ，则 f = w^Tx + b，那么对 w 求局部梯度则都为正，这样在反向传播的过程中 w 要么都往正方向更新，要么都往负方形更新，导致一种捆绑的效果，使得收敛缓慢。当然了，如果按照 batch 去训练，那么那个 batch 可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的梯度消失问题相比还是好很多的。

　　最后就是对其解析式中含有幂函数，计算机求解时相对比较耗时，对于规模比较大的深度网络，这会较大的增加训练时间。

科普：什么是饱和呢？

　　当一个激活函数 h(x) 满足：

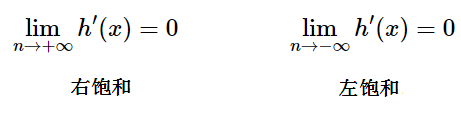
　　当 h(x) 即满足左饱和又满足又饱和，称之为饱和。

3.3 tanh函数

　　tanh是双曲函数中的一个，tanh() 为双曲正切，关于原点中心对称。在数学中，双曲正切 tanh 是由双曲正弦和双曲余弦这两者基本双曲函数推导而来。

　　正切函数时非常常见的激活函数，与Sigmoid函数相比，它的输出均值是0，使得其收敛速度要比Sigmoid快，减少迭代次数。相对于Sigmoid的好处是它的输出的均值为0，克服了第二点缺点。但是当饱和的时候还是会杀死梯度。

　　tanh激活函数和导函数分别如下：

　　对应的图像分别为：

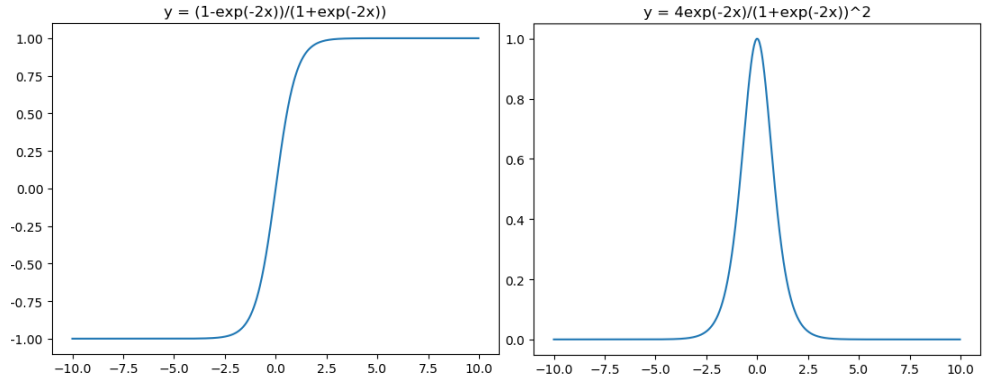
　　图像所对应的代码如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,(1-np.exp(-2*x))/(1+np.exp(-2*x)))
plt.title("y = (1-exp(-2x))/(1+exp(-2x))")
plt.show()

plt.plot(x,4*np.exp(-2*x)/(1+np.exp(-2*x))**2)
plt.title("y = 4exp(-2x)/(1+exp(-2x))^2")
plt.show()

　　在神经网络的应用中，tanh通常要优于Sigmoid的，因为 tanh的输出在 -1~1之间，均值为0，更方便下一层网络的学习。但是有一个例外，如果做二分类，输出层可以使用 Sigmoid，因为它可以算出属于某一类的概率。

　　tanh 读作 Hyperbolic Tangent，它解决了Sigmoid函数的不是 zero-centered 输出问题，tanh 函数将输入值压缩到 -1 和 1 之间，该函数与 Sigmoid 类似，也存在着梯度弥散或梯度饱和和幂运算的缺点。

为什么tanh 相比 Sigmoid收敛更快

　　1，梯度消失问题程度：

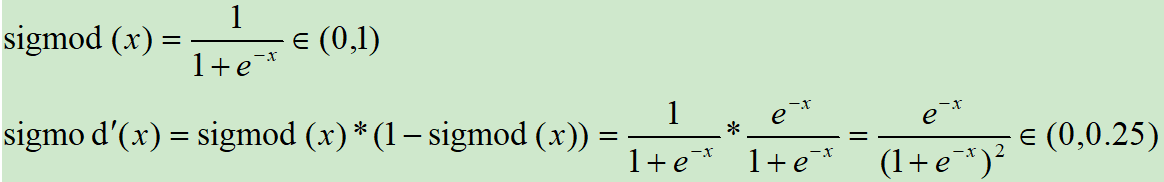
　　可以看出，tanh(x) 的梯度消失问题比 sigmoid要轻，梯度如果过早消失，收敛速度较慢。

　　2，以零为中心的影响，如果当前参数（w0, w1）的最佳优化方向是（+d0, -d1），则根据反向传播计算公式，我们希望x0和x1符号相反，但是如果上一级神经元采用 Sigmoid 函数作为激活函数，Sigmoid不以零为中心，输出值恒为正，那么我们无法进行更快的参数更新，而是走Z字形逼近最优解。

3.4，ReLU 函数

　　针对Sigmoid函数和tanh的缺点，提出ReLU函数。

　　线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。

　　最近几年比较受欢迎的一个激活函数，无饱和区，收敛快，计算简单，有时候会比较脆弱，如果变量的更新太快，还没有找到最佳值，就进入小于零的分段就会使得梯度变为零，无法更新直接死掉了。

　　ReLU激活函数和导函数分别为

　　对应的图像分别为：

　　图像对应的代码如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,np.clip(x,0,10e30))
plt.title("y = relu(x)=max(x,0)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,x>0,"o")
plt.title("y = relu'(x)")
plt.show()

　　解决了梯度消失现象，计算速度更快：

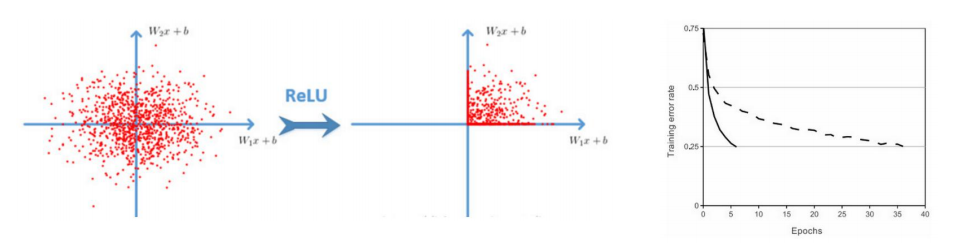
ReLU优点：

　　ReLU是修正线性单元（The Rectified Linear Unit）的简称，近些年来在深度学习中使用得很多，可以解决梯度弥散问题，ReLU函数就是一个取最大值函数，因为它的导数等于1或者就是0（注意：它并不是全区间可导的，但是我们可以取 Sub-gradient）。相对于sigmoid和tanh激励函数，对ReLU求梯度非常简单，计算也很简单，可以非常大程度地提升随机梯度下降的收敛速度。（因为ReLU是线性的，而sigmoid和tanh是非线性的）。所以它有以下几大优点：

1，解决了gradient vanishing （梯度消失）问题（在正区间）
2，计算方便，求导方便，计算速度非常快，只需要判断输入是否大于0
3，收敛速度远远大于 Sigmoid函数和 tanh函数，可以加速网络训练

ReLU缺点：
　　但ReLU的缺点是比较脆弱，随着训练的进行，可能会出现神经元死亡的情况，例如有一个很大的梯度流经ReLU单元后，那权重的更新结果可能是，在此之后任何的数据点都没有办法再激活它了。如果发生这种情况，那么流经神经元的梯度从这一点开始将永远是0。也就是说，ReLU神经元在训练中不可逆地死亡了。所以它的缺点如下：

1，由于负数部分恒为零，会导致一些神经元无法激活
2，输出不是以0为中心

　　ReLU的一个缺点是当x为负时导数等于零，但是在实践中没有问题，也可以使用leaky ReLU。总的来说，ReLU是神经网络中非常常用的激活函数。

　　ReLU 也有几个需要特别注意的问题：

　　1，ReLU 的输出不是 zero-centered

　　2，Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不会被更新，有两个主要原因可能导致这种情况产生：

　　（1）非常不幸的参数初始化，这种情况比较少见

　　（2） learning rate 太高，导致在训练过程中参数更新太大，不幸使网络进入这种状态。

　　解决方法是可以采用 Xavier 初始化方法，以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法。尽管存在这两个问题，ReLU目前仍然是最常见的 activation function，在搭建人工神经网络的时候推荐优先尝试。

ReLU 激活函数在零点是否可导？

　　答案是在零点不可导。

　　这里首先需要复习一些数学概念：连续与可导。

　　连续：设函数 y = f(x) 在点 x0 的某一领域内有定义，如果函数 y = f(x) 当 x——> x0 时的极限存在，且，则称函数 y = f(x) 在点 x0 处连续。

　　这里需要注意左极限等于右极限等于函数值，即，显然 ReLU函数是连续的在零点。但是不可导。

　　可导：设函数 y = f(x) 在点 x0 的某一邻域内有定义，则当自变量 x 在 x0 处取得增量 Δx 时，相应的 y 取增量；如果 Δx ——> 0 时， Δy / Δx 极限存在，则称 y= f(x) 在点 x0 处可导，并称这个极限为函数 y = f(x) 在点 x0 处的导数，记为：

　　然而左导数和右导数并不相等，因而函数在该处不可导，实际上，如果函数导数存在，当且仅当其左右导数均相等。

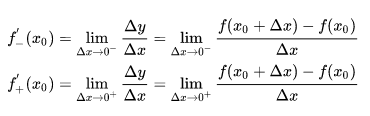
　　而 ReLU 左导数等于 0 ，右导数等于1，因此不可导。

ReLU 在零点不可导，那么在反向传播中如何处理？

　　caffe源码~/caffe/src/caffe/layers/relu_layer.cpp倒数第十行代码：

bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)+ negative_slope * (bottom_data[i] <= 0));

　　这句话就是说间断点的求导按左导数来计算。也就是默认情况下（negative_slope=0）,RELU的间断点处的导数认为是0。

3.5 Leaky ReLU 函数

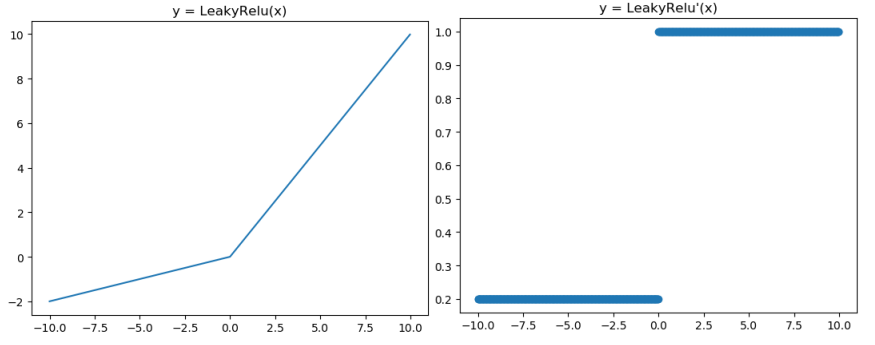
　　Leaky ReLU解决了ReLU会杀死一部分神经元的情况。Leaky ReLU 是给所有负值赋予一个非零斜率。Leaky ReLU 激活函数是在声学模型（2013）中首次提出。

　　Leaky ReLU激活函数和导函数如下：

　　对应的图像分别如下：

　　图像对应的代码如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
a = 0.2
plt.plot(x,x*np.clip((x>=0),a,1))
plt.title("y = LeakyRelu(x)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,np.clip((x>=0),a,1),"o")
plt.title("y = LeakyRelu'(x)")
plt.show()

　　人们为了解决 Dead ReLU Problem，提出了将 ReLU 的前半段设为 ax 而非0，通常 a = 0.01，另外一种直观的想法是基于参数的方法，即 ParmetricReLU ： f(x)=max(ax, x)，其中 a 可由方向传播算法学出来。理论上来说，Leaky ReLU 有ReLU的所有优点，外加不会有 Dead ReLU 问题，但是在实际操作当中，并没有完全证明 Leaky ReLU 总是好于 ReLU。

　　Leaky ReLU 主要是为了避免梯度消失，当神经元处于非激活状态时，允许一个非0的梯度存在，这样不会出现梯度消失，收敛速度快。他的优缺点和ReLU类似。

3.6 PReLU（参数化修正线性单元）

　　（Parametric Rectified Linear Unit），顾名思义：带参数的ReLU，二者定义和区别如下：

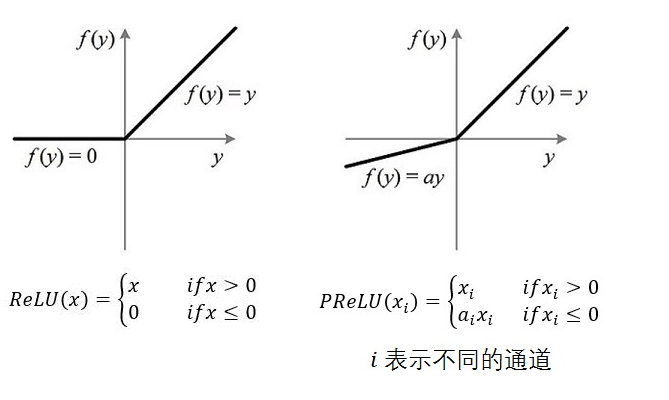
　　如果 ai=0，那么 PReLU 退化为 ReLU；如果ai 是一个很小的固定值（如 ai=0.01），则PReLU 退化为 Leaky ReLU（LReLU）。有实验证明：与 ReLU 相比，LReLU 对最终结果几乎没有什么影响。

　　关于 PReLU的几点说明：

1，PReLU 只增加了极少量的参数，也就意味着网络的计算量以及过拟合的危险性都只增加了一点。特别的，当不同的 channels 使用相同的 ai 时，参数就更少了。
2，当 BP 更新 ai 时，采用的是带动量的更新方式，如下图所示：

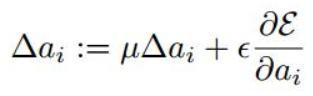
　　上面两个系数分别为动量和学习率。需要特别注意的是：更新 ai 时不施加权重衰减（L2正则化），因为这会把 ai 很大程度上 push 到 0，事实上，即使不加正则化，实验中 ai 也很少有超过1的。

3，整个论文 ai 被初始化为 0.25

　　总结来说：PReLU 可以看做 Leaky ReLU 的一个变体。在 PReLU中，负值部分的斜率是根据数据来定义的，而非预先定义的。作者称，在 ImageNet 分类（2015， Russakovsky等）上，PReLU 是超越人类分类水平的关键所在。

3.7 RReLU（随机矫正线性单元）

　　“随机矫正线性单元”，RReLU 也是 Leaky ReLU的一个变体。在 PReLU中，负值的斜率在训练中是随机的，在之后的测试中就变成了固定的了。RReLU 的亮点在于，在训练环节中，aji 是从一个均匀的分布 U(I, u) 中随机抽取的数值。形式上说，我们能得到以下结果：

　　下图为ReLU，LeakyReLU，PReLU，RReLU 的比较：

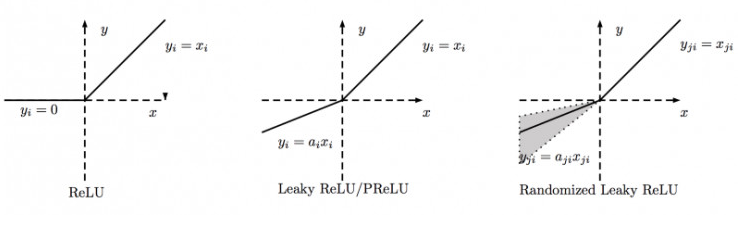
　　其中 PReLU 中的 ai 是根据数据变换的；Leaky ReLU中的 ai 是固定的；RReLU中的 aji 是在一个给定的范围内随机抽取的值，这个值在测试环境就会固定下来。

3.8 ReLU6 函数

　　ReLU 在 x > 0 的区域使用 x 进行线性激活，有可能造成激活后的值太大，影响模型的稳定性，为抵消 ReLU激活函数的线性增长部分，可以使用ReLU6函数。

　　MobileNetV1论文中使用了ReLU6作为激活函数，这个激活函数在 float16/int8 的嵌入式设备中效果很好，能较好的保持网络的鲁棒性。

　　ReLU6 就是普通的 ReLU，但是限制最大输出值为6（对输出值做 clip），这是为了在移动端设备 float16的低精度的时候，也能够有很好的数值分辨率，如果对ReLU的激活范围不加限制，输出范围为0到正无穷，如果激活值非常大，分布在一个很大的范围内，则低精度的 float16 无法很好地精确描述如此大范围的数值，带来精度损失。

　　ReLU6函数与其导函数如下：

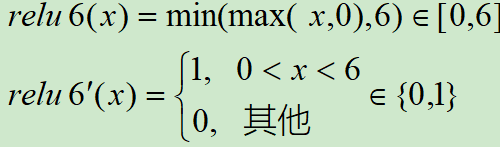
　　对应的图像分别如下：

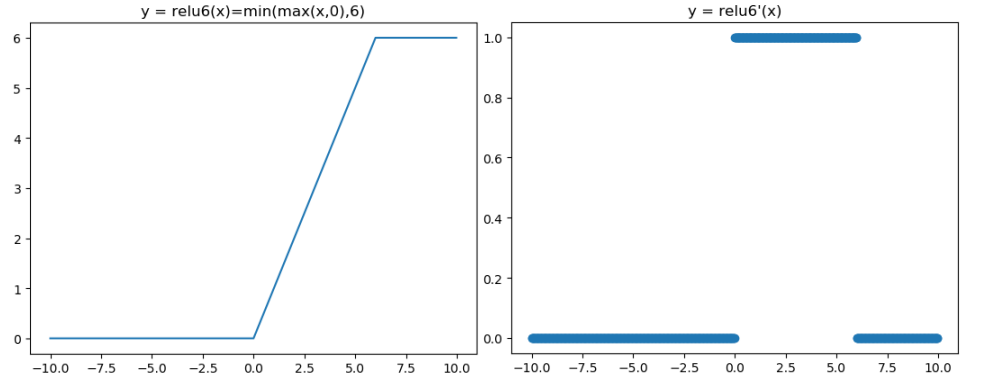
　　函数对应的代码如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,np.clip(x,0,6))
plt.title("y = relu6(x)=min(max(x,0),6)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,(x>0)&(x<6),"o")
plt.title("y = relu6'(x)")
plt.show()

3.9 ELU 函数（Exponential Linear Unit）

　　后面有人提出了一个 ReLU的进化版本叫 ELU，ELU就是 Exponential Linear Unit 的意思，如果它在大于 0 的地方跟其他的 ReLU 的家族是一样的，不一样的地方是在小于零的地方，它是 alpha 乘上 e 的 z 次方减去 1， z 就是那个激活函数的 Input，所以你可以想象说假设 z 等于 0 的时候， alpha=0，所以这边是接在一起的。而如果 z 趋向于负无穷大的时候， e 的负无穷大次方是零， 0-1=-1，然后再乘以 alpha，所以是 - alpha，所以如下图所示会收敛到 - alpha。

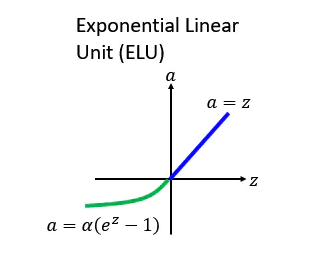
　　ELUs 是指“指数线性单元”，它试图将激活函数的平均值接近零，从而加速学习的速率。同时它融合了Sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性，则可以通过正值的标识来避免梯度消失的问题。根据一些研究，ELUs 分类精确度是高于 ReLUs的。

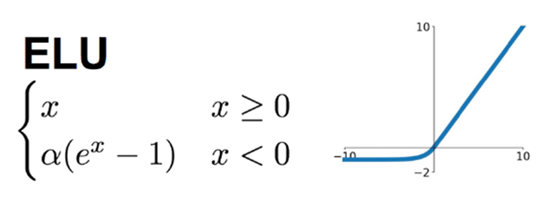
　　ELU在正值区间的值为x本身，这样减轻了梯度弥散问题（x>0区间导数处处为1），这点跟ReLU、Leaky ReLU相似。而在负值区间，ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

　　函数及导数的图像如下图所示：

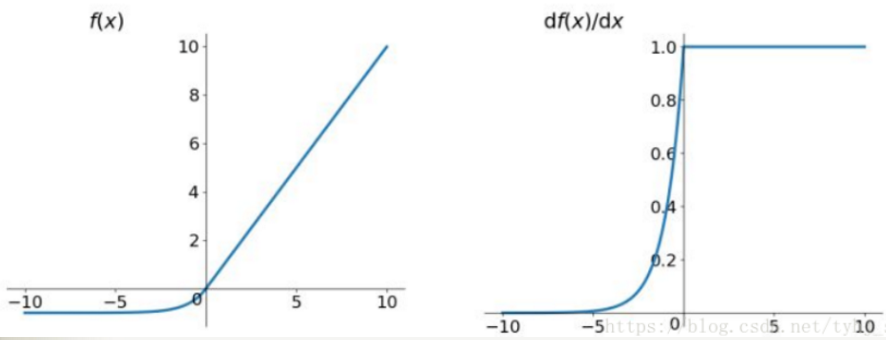
　　下图是ReLU、LReLU、ELU的曲线比较图：

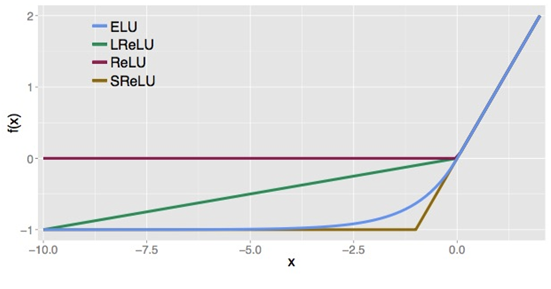
　　ELU 也是为了解决 ReLU 存在的问题而提出，显然，ELU有 ReLU的基本所有优点，以及不会出现Dead ReLU 问题，输出的均值接近0，zero-centered，它的一个小问题在于计算量稍大。类似于 Leaky ReLU ，理论上虽然好于 ReLU，但是实际使用中目前并没有好的证据 ELU 总是优于 ReLU。

3.10 SELU（Scaled ELU）

　　上面的 ELU，alpha要设置多少呢？这是个问题。

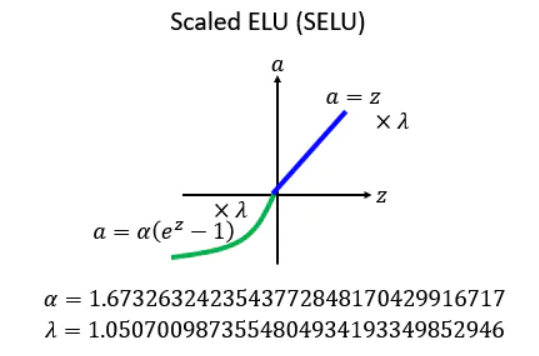
　　后面就出现了一种新的方法，叫做：SELU。它相当于对 ELU 做了一个新的变换：就是现在把每一个值的前面都乘上一个 lambda，然后告诉你 lambda和alpha应该设多少。

　　其中 alpha=1.67326324，lambda=1.050700987。

　　这个 alpha 和 lambda 的值的值看似是乱讲的，实际上是作者推导出来的，很麻烦的推导，详情也可以看作者的github：https://github.com/bioinf-jku/SNNs

3.11 Maxout 函数

　　这个函数可以参考论文《maxout networks》，Maxout 是深度学习网络中的一层网络，就像池化层，卷积层一样，我们可以把 maxout 看成是网络的激活函数层，我们假设网络某一层的输入特征向量为： X=(x1, x2, ....xd)，也就是我们输入的 d 个神经元，则maxout隐藏层中神经元的计算公式如下：

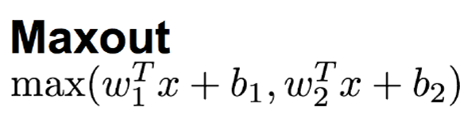
　　Maxout也是近些年非常流行的激励函数，简单来说，它是ReLU和Leaky ReLU的一个泛化版本，当w1、b1设置为0时，便转换为ReLU公式。

　　它用于RELU的优点而且没有死区，但是它的参数数量却增加了一倍。

　　因此，Maxout继承了ReLU的优点，同时又没有“一不小心就挂了”的担忧。但相比ReLU，因为有2次线性映射运算，因此计算量也会翻倍。

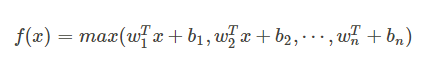
　　权重 w 是一个大小为（d, m , k）三维矩阵， b 是一个大小为（m, k）的二维矩阵，这两个就是我们需要学习的参数。如果我们设定参数为 k=1，那么这个时候，网络就类似于以前我们所学习的普通的 MLP网络。

　　我们可以这样理解，本来传统的 MLP 算法在第 i 层到第 i+1 层，参数只有一组，然而现在我们不这么干了，我们在这一层同时训练 n 组的 w, b 参数，然后选择激活值 Z 最大的作为下一层神经元的激活值，这个 max(Z) 函数即充当了激活函数。

3.12 Swish 激活函数

　　新的激活函数叫Swish，这个Swish激活函数是将 Sigmoid 乘上 z 得到它的 output。

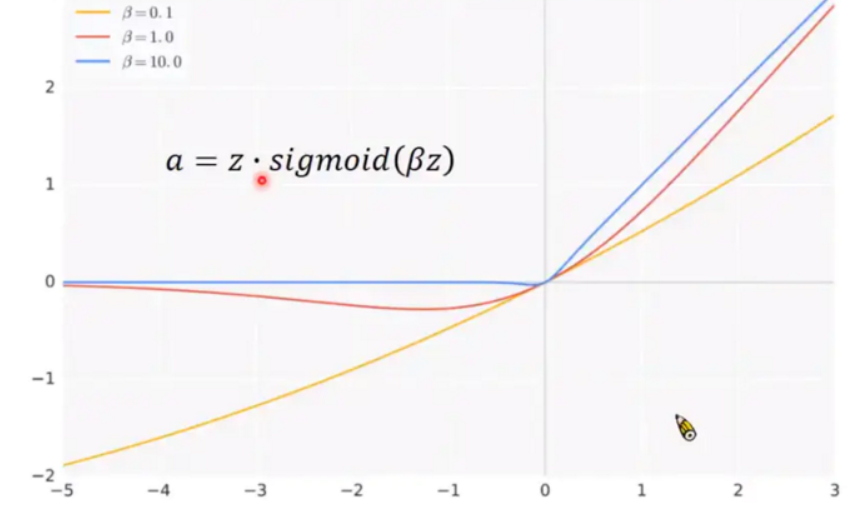
　　它中间有一个 beta 是可以调的，而 beta 设 1.0 的时候长这个样子，可以调配 beta 得到不同的形状。paper中 beta设为 1.0 的时候 performance 就已经不错了，所以这个是特别东西叫 swish。

3.13 Mish 激活函数

　　Mish 激活函数的表达式为：

　　使用 Matplotlib 画图可得：

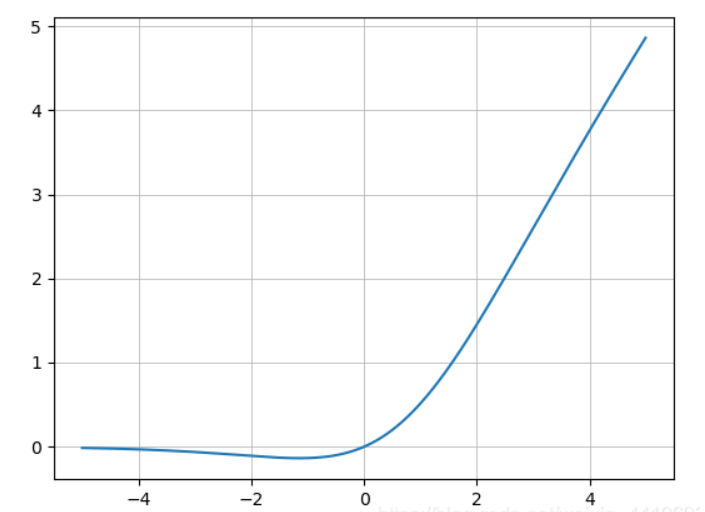
　　从图中可以看出它在负值时候并不是完全阶段，而是允许比较小的负梯度流入，从而保证信息流动。并且激活函数无边界这个特点，让他避免了饱和这一问题，比如 Sigmoid，tanh 激活函数通常存在梯度饱和问题，在两边极限的情况下，梯度趋近于1，而Mish 激活函数则巧妙的避开了这一点。另外 Mish 函数也保证了每一点的平滑，从而使得梯度下降效果比 ReLU要好。

　　代码：

Tensorflow：x = x *tf.math.tanh(F.softplus(x))

　　ReLU 有一些已知的弱点，但是通常它执行起来很轻，并且计算上很轻。Mish 具有较强的理论渊源，在测试中，就训练稳定性和准确性而言，Mish的平均性能优于 ReLU。

3.14 Softmax 函数

　　提起softmax函数，我们首先理清全连接层到损失层之间的计算，来看下面这幅图（侵删！）：

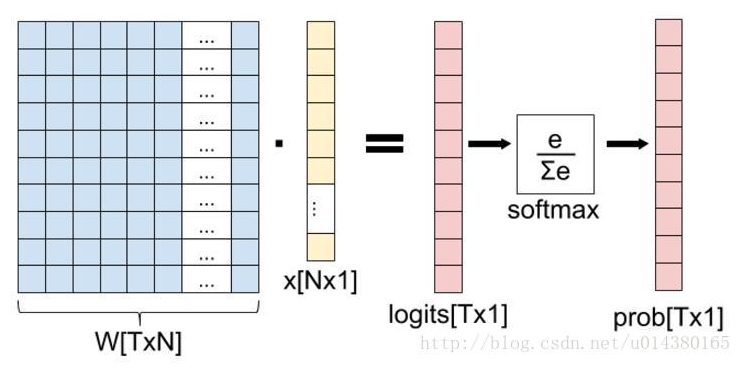
　　这张图的等号左边部分就是全连接层做的事，W是全连接层的参数，我们也称为权值，X是全连接层的输入，也就是特征。从图上可以看出特征X是N*1的向量，这是怎么得到的呢？这个特征就是由全连接层前面多个卷积层和池化层处理后得到的，假设全连接层前面连接的是一个卷积层，这个卷积层的输出是100个特征（也就是我们常说的feature map的channel为100），每个特征的大小是4*4，那么在将这些特征输入给全连接层之前会将这些特征flat成N*1的向量（这个时候N就是100*4*4=1600）。解释完X，再来看W，W是全连接层的参数，是个T*N的矩阵，这个N和X的N对应，T表示类别数，比如你是7分类，那么T就是7。我们所说的训练一个网络，对于全连接层而言就是寻找最合适的W矩阵。因此全连接层就是执行WX得到一个T*1的向量（也就是图中的logits[T*1]），这个向量里面的每个数都没有大小限制的，也就是从负无穷大到正无穷大。然后如果你是多分类问题，一般会在全连接层后面接一个softmax层，这个softmax的输入是T*1的向量，输出也是T*1的向量（也就是图中的prob[T*1]，这个向量的每个值表示这个样本属于每个类的概率），只不过输出的向量的每个值的大小范围为0到1。

　　现在知道softmax的输出向量的意思了，就是概率，该样本属于各个类的概率！

　　softmax 函数，又称为归一化指数函数。它是二分类函数 Sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来，下图展示了softmax的计算方法：

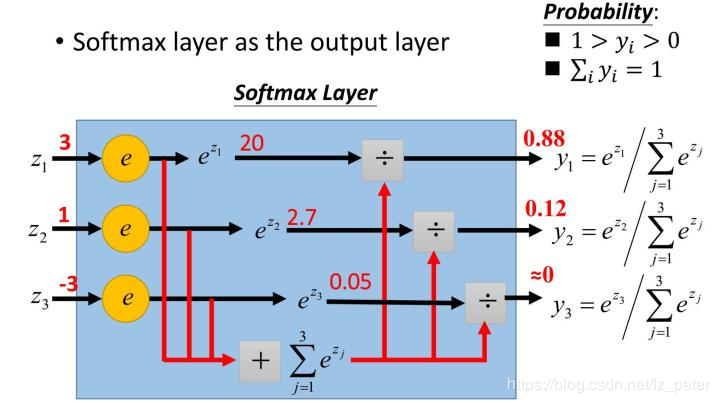
　　那么为什么softmax是这种形式呢？

　　首先，我们知道概率有两个性质：1，预测的概率为非负数‘2，各种预测结果概率之和等于1.

softmax 就是将在负无穷到正无穷上的预测结果按照这两步转换为概率的。

3.14.1 将预测结果转化为非负数。

　　下图是 y=exp(x) 的图像，我们可以知道指数函数的值域取值范围是零到正无穷，softmax第一步就是将模型的预测结果转化到指数函数上，这样保证了概率的非负性。

3.14.2 各种预测结果概率之和等于1

　　为了确保各个预测结果的概率之和等于1，我们只需要将转换后的结果进行归一化处理。方法就是将转化后的结果除以所有转化后结果之和，可以理解为转化后结果占总数的百分比。这样就得到了近似的概率。

　　简单举个例子：

　　假如模型对一个三分类问题的预测结果为-3、1.5、2.7。我们要用softmax将模型结果转为概率。步骤如下：

　　1）将预测结果转化为非负数

y1 = exp(x1) = exp(-3) = 0.05

y2 = exp(x2) = exp(1.5) = 4.48

y3 = exp(x3) = exp(2.7) = 14.88

　　2）各种预测结果概率之和等于1

z1 = y1/(y1+y2+y3) = 0.05/(0.05+4.48+14.88) = 0.0026

z2 = y2/(y1+y2+y3) = 4.48/(0.05+4.48+14.88) = 0.2308

z3 = y3/(y1+y2+y3) = 14.88/(0.05+4.48+14.88) = 0.7666

　　总结一下，softmax如何将多分类输出转换为概率，可以分为两步：

1，分子：通过指数函数，将实数输出映射到零到正无穷
2，分母：将所有结果相加，进行归一化

　　下面是斯坦福大学 CS224n 课程中最 softmax的解释：

3.15 Softplus函数

　　函数如下：

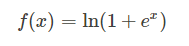
　　函数图：

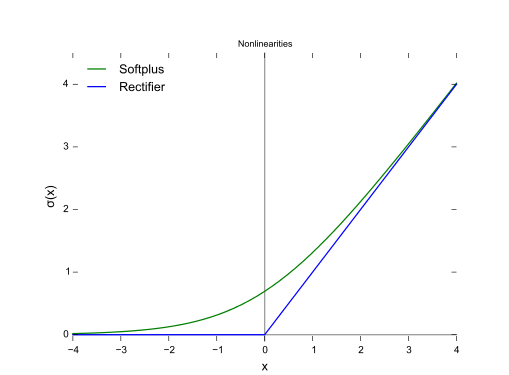
3.16 GELU函数

　　参考链接：https://alaaalatif.github.io/2019-04-11-gelu/

　　GELU 激活函数是使用在Google AI's BERT 和 OpenAI's GPT模型，这些模型的结果在各种各样的NLP任务中都达到了 SOTA的结果。

　　GELU的使用技巧：当训练过程中使用gelu作为激活函数进行训练的时候，建议使用一个带有动量（momentum）的优化器。

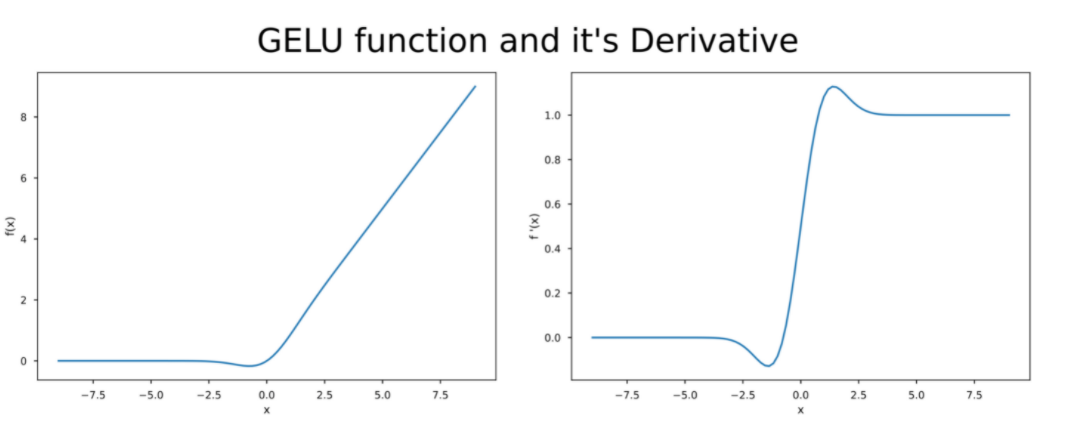
　　GELU激活函数公式如下：

　　x是输入值，而X是具有零均值和单位方差的高斯随机变量。 P(X<=x) 是X小于或等于给定值x的概率。

　　而GELU激活函数的导数：

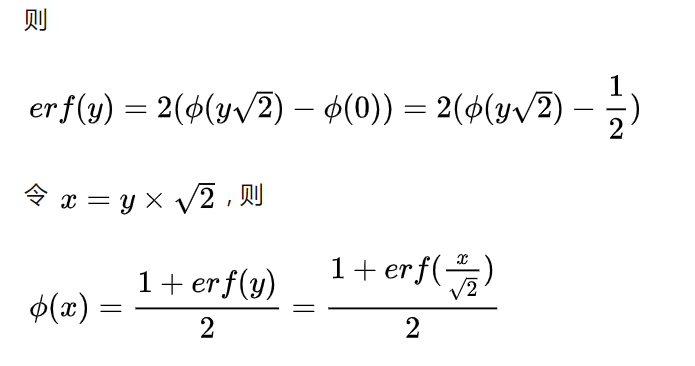
　　GELU的激活函数和其导数的可视化如下：

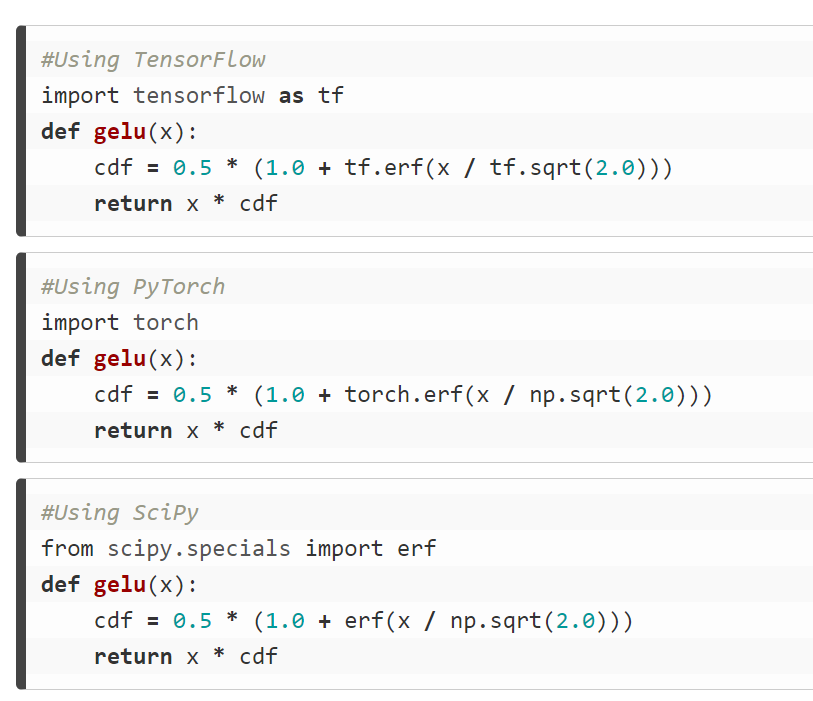
　　代码实现如下：

4，如何选择合适的激活函数

　　一般我们可以这样：

1，首先尝试ReLU，速度快，但是要注意训练的状态
2，如果ReLU效果欠佳，尝试Leaky ReLU 或者 Maxout 等变种
3，尝试 tanh正切函数（以零为中心，零点处梯度为1）
4，Sigmoid tanh 在RMM（LSTM 注意力机制等）结构中有所应用，作为门控或者概率值
5，在浅层神经网络中，如不超过四层，可选择使用多种激励函数，没有太大的影响

　　深度学习中往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用 zero-centered 数据（可以经过数据预处理实现）和 zero-centered 输出。所以要尽量选择输出具有 zero-centered 特点的激活函数以加快模型的收敛速度。

　　如果是使用 ReLU，那么一定要小心设置 learning rate，而且要注意，不要让网络出现很多“dead”神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU ,PReLU , 或者 Maxout。

　　最好不要用 Sigmoid函数，不过可以试试 tanh，不过可以预期它的效果会比不上 ReLU和 maxout。

5，Keras封装的激活函数

　　部分代码如下：

"""Built-in activation functions.
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import six
import warnings
from . import backend as K
from .utils.generic_utils import deserialize_keras_object
from .engine import Layer


def softmax(x, axis=-1):
    """Softmax activation function.

    # Arguments
        x: Input tensor.
        axis: Integer, axis along which the softmax normalization is applied.

    # Returns
        Tensor, output of softmax transformation.

    # Raises
        ValueError: In case `dim(x) == 1`.
    """
    ndim = K.ndim(x)
    if ndim == 1:
        raise ValueError('Cannot apply softmax to a tensor that is 1D')
    elif ndim == 2:
        return K.softmax(x)
    elif ndim > 2:
        e = K.exp(x - K.max(x, axis=axis, keepdims=True))
        s = K.sum(e, axis=axis, keepdims=True)
        return e / s
    else:
        raise ValueError('Cannot apply softmax to a tensor that is 1D. '
                         'Received input: %s' % x)


def elu(x, alpha=1.0):
    """Exponential linear unit.

    # Arguments
        x: Input tensor.
        alpha: A scalar, slope of negative section.

    # Returns
        The exponential linear activation: `x` if `x > 0` and
        `alpha * (exp(x)-1)` if `x < 0`.

    # References
        - [Fast and Accurate Deep Network Learning by Exponential
        Linear Units (ELUs)](https://arxiv.org/abs/1511.07289)
    """
    return K.elu(x, alpha)


def selu(x):
    """Scaled Exponential Linear Unit (SELU).

    SELU is equal to: `scale * elu(x, alpha)`, where alpha and scale
    are pre-defined constants. The values of `alpha` and `scale` are
    chosen so that the mean and variance of the inputs are preserved
    between two consecutive layers as long as the weights are initialized
    correctly (see `lecun_normal` initialization) and the number of inputs
    is "large enough" (see references for more information).

    # Arguments
        x: A tensor or variable to compute the activation function for.

    # Returns
       The scaled exponential unit activation: `scale * elu(x, alpha)`.

    # Note
        - To be used together with the initialization "lecun_normal".
        - To be used together with the dropout variant "AlphaDropout".

    # References
        - [Self-Normalizing Neural Networks](https://arxiv.org/abs/1706.02515)
    """
    alpha = 1.6732632423543772848170429916717
    scale = 1.0507009873554804934193349852946
    return scale * K.elu(x, alpha)


def softplus(x):
    """Softplus activation function.

    # Arguments
        x: Input tensor.

    # Returns
        The softplus activation: `log(exp(x) + 1)`.
    """
    return K.softplus(x)


def softsign(x):
    """Softsign activation function.

    # Arguments
        x: Input tensor.

    # Returns
        The softplus activation: `x / (abs(x) + 1)`.
    """
    return K.softsign(x)


def relu(x, alpha=0., max_value=None, threshold=0.):
    """Rectified Linear Unit.

    With default values, it returns element-wise `max(x, 0)`.

    Otherwise, it follows:
    `f(x) = max_value` for `x >= max_value`,
    `f(x) = x` for `threshold <= x < max_value`,
    `f(x) = alpha * (x - threshold)` otherwise.

    # Arguments
        x: Input tensor.
        alpha: float. Slope of the negative part. Defaults to zero.
        max_value: float. Saturation threshold.
        threshold: float. Threshold value for thresholded activation.

    # Returns
        A tensor.
    """
    return K.relu(x, alpha=alpha, max_value=max_value, threshold=threshold)


def tanh(x):
    """Hyperbolic tangent activation function.
    """
    return K.tanh(x)


def sigmoid(x):
    """Sigmoid activation function.
    """
    return K.sigmoid(x)


def hard_sigmoid(x):
    """Hard sigmoid activation function.

    Faster to compute than sigmoid activation.

    # Arguments
        x: Input tensor.

    # Returns
        Hard sigmoid activation:

        - `0` if `x < -2.5`
        - `1` if `x > 2.5`
        - `0.2 * x + 0.5` if `-2.5 <= x <= 2.5`.
    """
    return K.hard_sigmoid(x)


def exponential(x):
    """Exponential (base e) activation function.
    """
    return K.exp(x)


def linear(x):
    """Linear (i.e. identity) activation function.
    """
    return x


def serialize(activation):
    return activation.__name__


def deserialize(name, custom_objects=None):
    return deserialize_keras_object(
        name,
        module_objects=globals(),
        custom_objects=custom_objects,
        printable_module_name='activation function')


def get(identifier):
    """Get the `identifier` activation function.

    # Arguments
        identifier: None or str, name of the function.

    # Returns
        The activation function, `linear` if `identifier` is None.

    # Raises
        ValueError if unknown identifier
    """
    if identifier is None:
        return linear
    if isinstance(identifier, six.string_types):
        identifier = str(identifier)
        return deserialize(identifier)
    elif callable(identifier):
        if isinstance(identifier, Layer):
            warnings.warn(
                'Do not pass a layer instance (such as {identifier}) as the '
                'activation argument of another layer. Instead, advanced '
                'activation layers should be used just like any other '
                'layer in a model.'.format(
                    identifier=identifier.__class__.__name__))
        return identifier
    else:
        raise ValueError('Could not interpret '
                         'activation function identifier:', identifier)

　　这篇笔记是整理网上优秀博主的博客，然后加上自己的理解，整理于此，主要是方便自己，方便别人查询学习，仅此而已。

参考文献：https://my.oschina.net/u/876354/blog/1624376

https://www.wandouip.com/t5i356161/

https://blog.csdn.net/lz_peter/article/details/84574716

https://www.bbsmax.com/A/QV5Zyg6nJy/

https://www.cnblogs.com/ziytong/p/12820738.html

posted @ 2020-08-15 14:33 战争热诚阅读(12316) 评论(0) 编辑收藏举报

刷新页面返回顶部

战争热诚