OpenCV计算机视觉学习（10）——图像变换（傅里叶变换，高通滤波，低通滤波）

如果需要处理的原图及代码，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/ComputerVisionPractice

　　在数字图像处理中，有两个经典的变换被广泛应用——傅里叶变换和霍夫变化。其中，傅里叶变换主要是将时间域上的信号转变为频率域上的信号，用来进行图像降噪，图像增强等处理，这一篇主要学习傅里叶变换，后面在学习霍夫变换。

　　下面学习一下傅里叶变换。有人说傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式（出处（强烈建议看这篇文章）：https://zhuanlan.zhihu.com/p/19763358）

　　傅里叶变换的作用：

　　对于数字图像这种离散的信号，频率大小表示信号变换的剧烈程度或者说信号变化的快慢。频率越大，变换越剧烈，频率越小，信号越平缓，对应到的图像中，高频信号往往是图像中的边缘信号和噪声信号，而低频信号包含图像变化频繁的图像轮廓及背景灯信号。

　　需要说明的是：傅里叶变换得到的频谱图上的点与原图像上的点之间不存在一一对应的关系。

• 高频：变换剧烈的灰度分量，例如边界
• 低频：变换缓慢的灰度分量，例如一片大海

　　滤波器：

• 低通滤波器：只保留低频，会使得图像模糊
• 高频滤波器：只保留高频，会使得图像细节增强

　　不懂的话，可以看之前文章中粘贴的一幅图，这里再粘贴一下：

具体模糊和滤波的关系如下图（https://www.zhihu.com/question/54918332/answer/142137732）：

1，频域及其频域数据的应用

1.1  什么是频域

　　从我们出世，我们看到的世界都是以时间贯穿，股票的走势，人的身高，汽车的轨迹都会随着时间发生变换。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会停止下来。但是我们可以用另一种方法观察世界的话，你可以发现世界是永恒不变的，而这个静止的世界就叫做频域。

　　正式定义：频域是描述信号在频率方面特性时用到的一种坐标系。在电子学，控制系统工程和统计学中，频域图显示了一个在频率范围内每个给定频带内的信号量。

　　下面举个例子：

　　我们普通人对音乐的理解是什么呢？可能如下图：

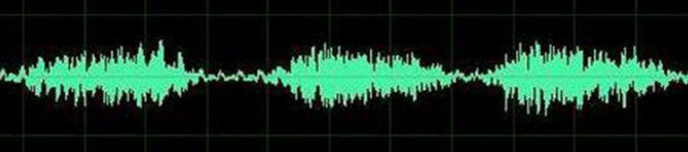
　　上图是我们对音乐最普遍的理解，一个随着时间变化的震动。但是我相信对于乐手来说，音乐更直观的理解是这样的：

 　　下面我们将两个图简化，借用百度百科的正弦函数在时域和频域的表现如下：

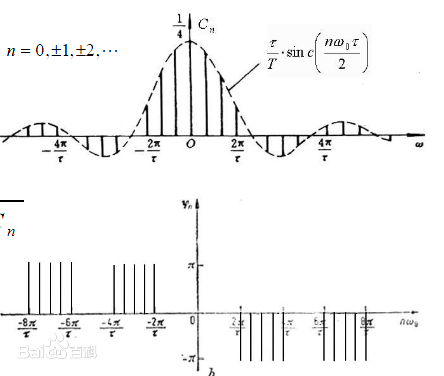
　　总结来说，在时域我们观察到钢琴的琴弦一会上一会下的摆动，如同上图上一样的走势，而在频域，就只是永恒的，如上图下一样。而贯穿时域与频域的方法之一，就是傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换（Fourier Transformation）。

1.2  频域数据的应用

图像去噪

　　我们可以根据需要获得在频域对图像进行处理，比如在需要除去图像中的噪声时，我们可以设计一个低通滤波器，去掉图像中的高频噪声，但是往往也会抑制图像的边缘信息，这就是造成图像模糊的原因。以均值滤波为例，用均值模板与图像做卷积，大家都知道，在空间域做卷积，相当于在频域做乘积，而均值模板在频域是没有高频信号的，只有一个常量的分量，所以均值模板是对图像局部做低通滤波。除此之外，常见的高斯滤波也是一种低通滤波器，因为高斯函数经过傅里叶变换后，在频域的分布依然服从高斯分布，如下图所示，所以它对高频信息有很好的滤除效果。

 

图像增强及锐化

　　图像增强需要增强图像的细节，而图像的细节往往就是图像中高频的部分，所以增强图像中的高频信息能够达到图像增强的目的。

　　同样的图像锐化的目的是使模糊的图像变得更加清晰，其主要方式是增强图像的边缘部分，其实就是增强图像中灰度变化剧烈的部分，所以通过增强图像中的高频信息能够增强图像边缘，从而达到图像锐化的目的。从这里可以看出，可以通过提取图像中的高频信号来得到图像的边缘和纹理信息。

2，傅里叶变换原理

2.1 举例分析傅里叶变换

　　傅里叶变换（Fourier Transform，简称FT）常用于数字信号处理，它的目的是将时间域上的信号转变为频率域上的信号。随着域的不同，对同一个事物的了解角度也随之改变，因此在时域某些不好处理的地方，在频域就可以较为简单的处理。同时，可以从频域里发现一些原先不易察觉的特征。傅里叶定理指出“任何连续周期信号都可以表示成（或者无限逼近）一系列正弦信号的叠加”。

 　　下面引用“Python + OpenCV图像处理课程”（地址在文末给出）中的一个案例，他将某饮料的制作过程的时域角度转换为频域角度。

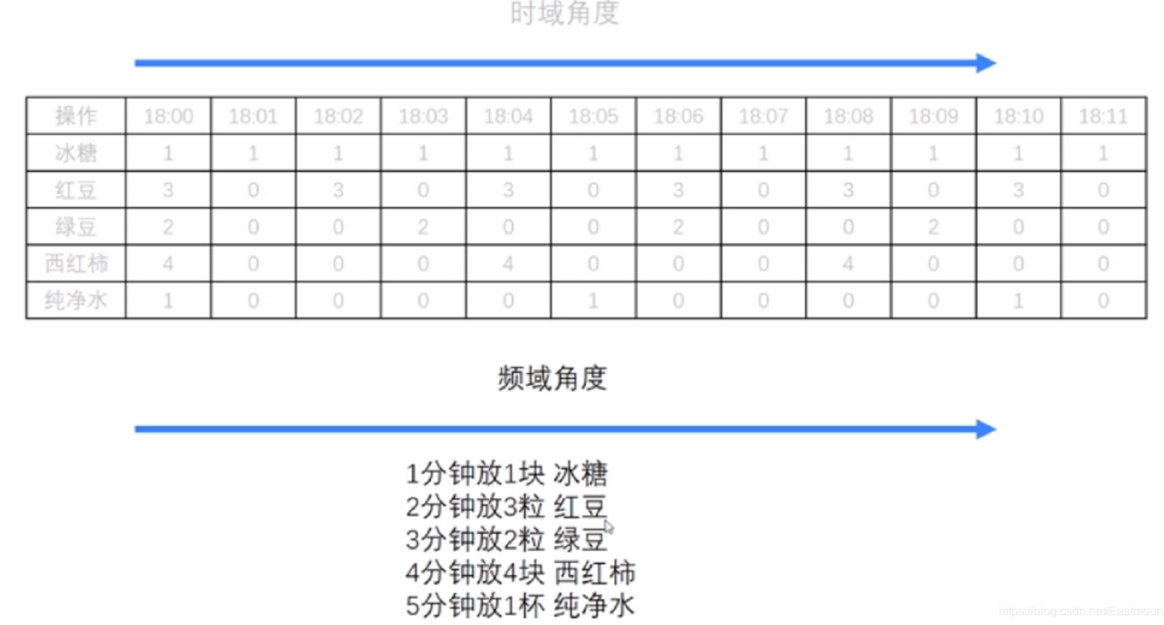
 　　绘制对应的时间图和频率图如下所示：

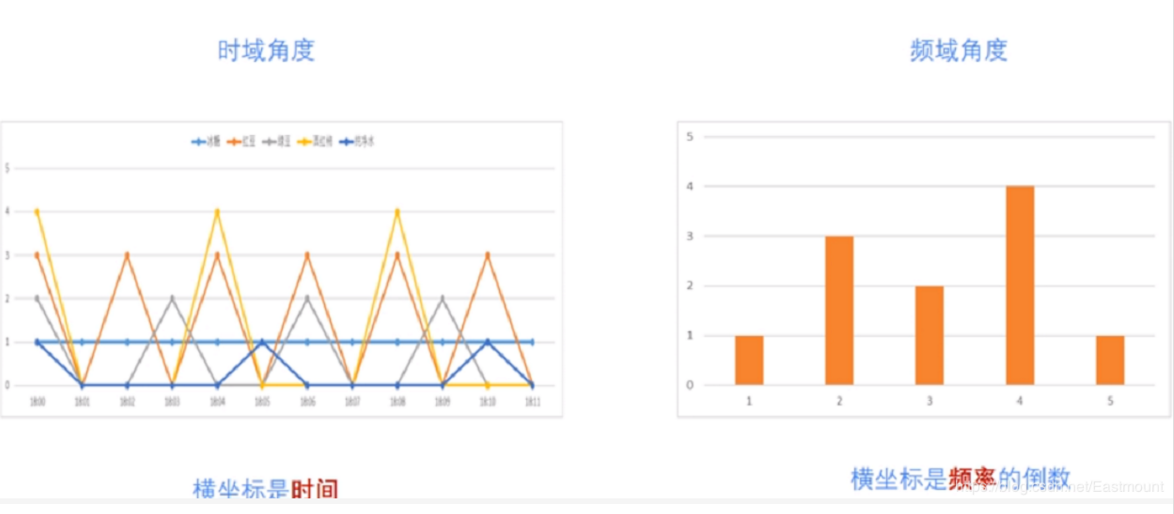
 　　傅里叶公式如下，其中 w 表示频率，t 表示时间，为复变函数。它将时间域的函数表示为频率域的函数 f(t) 的积分。

　　傅里叶变换认为一个周期函数（信号）包含多个频率分量，任意函数（信号） f(t) 可通过多个周期函数（或基函数）相加合成。从物理角度理解，傅里叶变换是以一组特殊的函数（三角函数）为正交基，对原函数进行线性变换，物理意义便是原函数在各组基函数的投影。如下图所示，它是由三条正弦曲线组成：

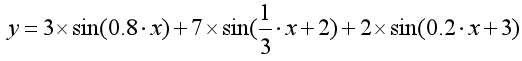
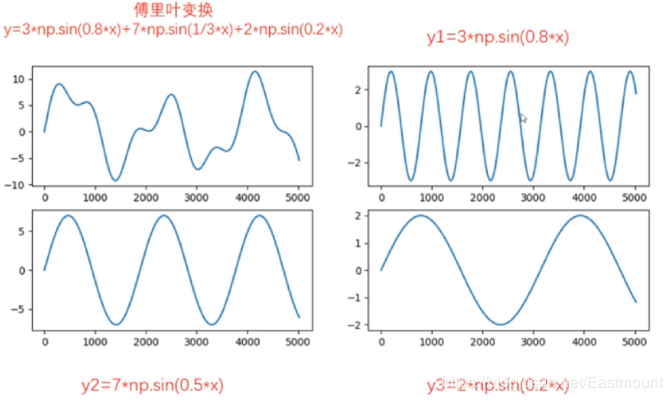　　傅里叶变换可以应用于图像处理中，经过对图像进行变换得到其频谱图。从频谱图里频率高低来表征图像中灰度变化剧烈程度。图像中的边缘信号和噪声信号往往是高频信号，而图像变换频繁的图像轮廓及背景等信号往往是低频信号。这时可以有针对性的对图像进行相关操作，例如图像除噪，图像增强和锐化等。

　　二维图像的傅里叶变换可以用以下数学公式表示，其中 f 是空间域（Spatial Domain）的值， F 是频域（Frequency Domain）值

2.2  二维傅里叶变换的定义

　　上面其实已经引出了二维傅里叶变换，这里详细学习一下。

　　首先我们看一下连续型二维傅里叶变换：

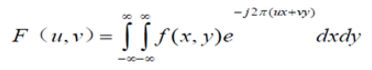
　　连续型二维傅里叶变换的逆变换：

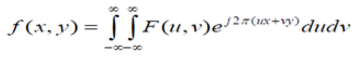
　　下面看一下离散型二维傅里叶变换（当我们定义图像尺寸为M*N，则函数的离散傅里叶变换由以下等式给出）：

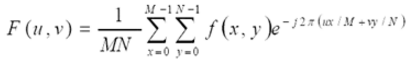
　　离散傅里叶逆变换由下式给出：

　　令R和I分别表示F的实部和虚部，则傅里叶频谱，相位角，功率谱（幅度）定义如下：

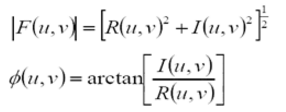
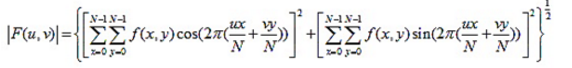
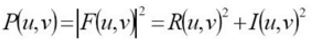
2.3  用 FFT 计算二维离散傅里叶变换

　　二维离散傅里叶变换的定义为：

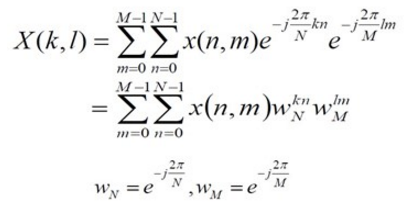　　二维离散傅里叶变换可通过两次一维离散傅里叶变换来实现：

　　（1）做一维N点DFT（对每个 m 做一次，共 M 次）

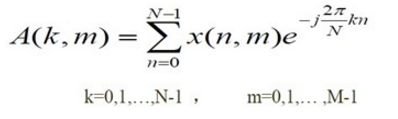
　　（2）作M点的DFT（对每个k做一次，共N次）

　　这两次离散傅里叶变换都可以用快速算法求得，若M和N都是2的幂，则可以使用基二FFT算法，所需要乘法次数为：

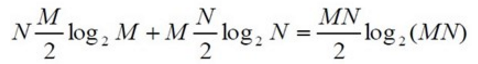
　　而直接计算二维离散傅里叶变换所需要的乘法次数为（M+N）MN，当M和N比较大用FFT运算，可节约很多运算量。

2.4  图像傅里叶变换的物理意义

　　图像的频率是表征图像中灰度变换剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。傅里叶变换在实际中有明显的物理意义，设f 是一个能量有限的模拟信号，则其傅里叶变换就表示 f 的频谱。从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果来看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数。

　　傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数傅里叶变换以前，图像（未压缩的位图）是由对在连续空间（现实空间）上的采样得到一系列的集合，通常用一个二维矩阵表示空间上各点，记为 z=f(x, y)。又因为空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就必须由梯度来表示，这样我们才能通过观察图像得知物体在三维空间中的对应关系。

　　傅里叶频谱图上我们看到的明暗不一的亮点，其意义是指图像上某一点与领域点差异的强弱，即梯度的大小。也即该点的频率的大小（可以这么理解，图像中低频部分指低梯度的点，高频部分相反）。一般来说，梯度大则该点的亮度强，否则该点的亮度弱。这样通过观察傅里叶变换后的频谱图，也叫功率图，我们就可以直观的看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与领域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。

　　对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰的看出图像频率分布以外，还有一个好处，它可以分离出周期性规律的干扰信号，比如正弦干扰。一幅频谱图如果带有正弦干扰，移频到原点上就可以看出，除了中心以外还存在以另一点为中心，对称分布的亮点集合，这个集合就是干扰噪音产生的。这时可以很直观的通过在该位置放置带阻滤波器消除干扰。

　　对上面的傅里叶变换有了大致的了解之后，下面通过Numpy和OpenCV分别学习图像傅里叶变换的算法及操作代码。

2.5  二维傅里叶变换的性质

分离性

　　二维离散傅里叶变换具有分离性

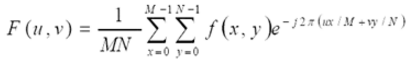
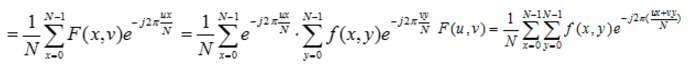
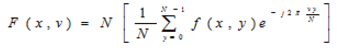
　　分离性质的主要优点是可借助一系列一维傅里叶变换分两步求得。第一步，沿着的每一行取变换，将其结果乘以 1/N，取得二维函数；第二步，沿着的每一列取变换，再将结果乘以 1/N就得到了。这种方法是先行后列。如果采用先列后行的顺序，其结果相同。

　　如图：

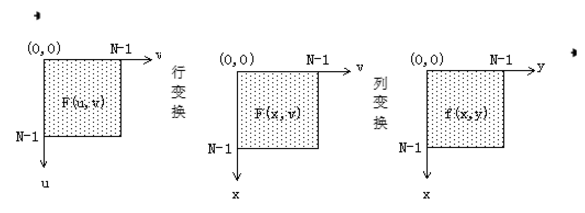
　　对逆变换 f(x, y) 也可以类似的分两步进行：

 平移性

　　傅里叶变换和逆变换对的位移性质是指：

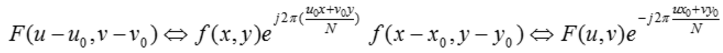
　　由乘以指数项并取其乘积的傅里叶变换，使频率平面的原点位移至。同样的，以指数项乘以并取其反变换，将空间域平面的原点位移至当 N/2时，指数项为：

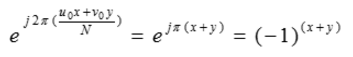
　　即为：

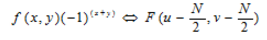
　　这样，用（x+y）乘以就可以将的傅里叶变换原点移动到 N*N 频率方阵的中心，这样才能看到整个谱图。另外，对的平移不影响其傅里叶变换的幅值。

　　此外，与连续二维傅里叶变换一样，二维离散傅里叶变换也具有周期性，共轭对称性，线性，旋转性，相关定理，卷积定理，比例性等性质。这些性质在分析以及处理图像时有重要意义。

2.6  二维离散傅里叶变换的图像性质

　　1，图像经过二维傅里叶的变换后，其变换稀疏矩阵具有如下性质：若交换矩阵原点设在中心，其频谱能量集中分布在变换稀疏矩阵的中心附近。若所用的二维傅里叶变换矩阵的云巅设在左上角，那么图像信号能量将集中在系数矩阵的四个角上。这是由二维傅里叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。

　　2，图像灰度变化缓慢的区域，对应它变换后的低频分量部分；图像灰度呈阶跃变化的区域，对应变换后的高频分量部分。除颗粒噪音外，图像细节的边缘，轮廓处都是灰度变换突变区域，他们都具有变换后的高频分量特征。

3，傅里叶变换的实现

　　注意：无论是numpy实现，还是OpenCV实现，得到的结果中频率为0的部分都会在左上角，通常要转换到中心位置，可以通过shift变换来实现。

3.1 Numpy实现傅里叶变换

　　Numpy的 FFT 包提供了函数 np.fft.fft2() 可以对信号进行快速傅里叶变换，其函数原型如下所示（该函数的输出结果是一个复数数组complex ndarray）

fft2(a, s=None, axes=(-2, -1), norm=None)

 　　参数意义：

• a表示输入图像，阵列状的复杂数组
• s表示整数序列，可以决定输出数组的大小。输出可选形状（每个转换轴的长度），其中s[0]表示轴0，s[1]表示轴1。对应fit(x,n)函数中的n，沿着每个轴，如果给定的形状小于输入形状，则将剪切输入。如果大于则输入将用零填充。如果未给定’s’，则使用沿’axles’指定的轴的输入形状
• axes表示整数序列，用于计算FFT的可选轴。如果未给出，则使用最后两个轴。“axes”中的重复索引表示对该轴执行多次转换，一个元素序列意味着执行一维FFT
• norm包括None和ortho两个选项，规范化模式（请参见numpy.fft）。默认值为无

　　Numpy中fft模块有很多函数，相关函数如下：

#计算一维傅里叶变换
numpy.fft.fft(a, n=None, axis=-1, norm=None)

#计算二维的傅里叶变换
numpy.fft.fft2(a, n=None, axis=-1, norm=None)

#计算n维的傅里叶变换
numpy.fft.fftn()

#计算n维实数的傅里叶变换
numpy.fft.rfftn()

#返回傅里叶变换的采样频率
numpy.fft.fftfreq()

#将FFT输出中的直流分量移动到频谱中央
numpy.fft.shift()

 　　下面的代码是通过Numpy实现傅里叶变换，调用 np.fft.fft2() 快速傅里叶变换得到频率分布，接着调用 np.fft.fftshift() 函数将中心位置转移至中间，最终通过 Matplotlib显示效果图。

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 读取图像
img = cv2.imread('irving.jpg', )
# 图像进行灰度化处理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 快速傅里叶变换算法得到频率分布
f = np.fft.fft2(img)

# 默认结果中心点位置是在左上角
# 调用fftshift()函数转移到中间位置
fshift = np.fft.fftshift(f)

# fft 结果是复数，其绝对值结果是振幅
fimg = np.log(np.abs(fshift))

# 展示结果
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('original Fourier')
plt.axis('off')
plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('fourier Fourier')
plt.axis('off')
plt.show()

 　　结果如下：

 　　我们从上面结果看到，左边为原始图像，右边为频率分布图谱，其中越靠近中心位置频率越低，越亮（灰度值越高）的位置代表该频率的信息振幅越大。

3.2  OpenCV实现傅里叶变换

　　OpenCV中实现傅里叶变换的函数是 cv2.dft()，他和Numpy输出的结果是一样的，但是是双通道的。第一个通道是结果的实数部分，第二个通道是结果的虚数部分，并且输入图像要首先转换成  np.float32格式。其函数原型如下：

dst = cv2.dft(src, dst=None, flags=None, nonzeroRows=None)

 　　参数含义：

• src表示输入图像，需要通过np.float32转换格式
• dst表示输出图像，包括输出大小和尺寸flags表示转换标记，其中：

　　　　DFT _INVERSE执行反向一维或二维转换，而不是默认的正向转换；

　　　　DFT _SCALE表示缩放结果，由阵列元素的数量除以它；

　　　　DFT _ROWS执行正向或反向变换输入矩阵的每个单独的行，该标志可以同时转换多个矢量，并可用于减少开销以执行3D和更高维度的转换等；

　　　　DFT _COMPLEX_OUTPUT执行1D或2D实数组的正向转换，这是最快的选择，默认功能；

　　　　DFT _REAL_OUTPUT执行一维或二维复数阵列的逆变换，结果通常是相同大小的复数数组，但如果输入数组具有共轭复数对称性，则输出为真实数组

• nonzeroRows表示当参数不为零时，函数假定只有nonzeroRows输入数组的第一行（未设置）或者只有输出数组的第一个（设置）包含非零，因此函数可以处理其余的行更有效率，并节省一些时间；这种技术对计算阵列互相关或使用DFT卷积非常有用

　　注意：由于输出的频谱结果是一个复数，需要调用 cv2.magnitude() 函数将傅里叶变换的双通达结果转换为0到255的范围。其函数原型如下：

cv2.magnitude(x, y, magnitude=None)

 　　参数意义：

• x表示浮点型X坐标值，即实部
• y表示浮点型Y坐标值，即虚部
  最终输出结果为幅值，即：

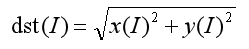
　　完整代码如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 读取图像
img = cv2.imread('irving.jpg', )
# 图像进行灰度化处理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅里叶变换
# cv2.DFT_COMPLEX_OUTPUT 执行一维或二维复数阵列的逆变换，结果通常是相同大小的复数数组
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)

# 将频谱低频从左上角移动到中心位置
dft_shift = np.fft.fftshift(dft)

# 频谱图像双通道复数转换为0~255区间
result = 10 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 显示图像
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input image')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(result, cmap='gray')
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()

 　　结果如下：

 　　上图左边为原始图，右边为转换后的频谱图像，并且保证低频位于中心位置。

4，傅里叶逆变换的实现

　　注意：无论是numpy实现，还是OpenCV实现，得到的结果中频率为0的部分都会在左上角，通常要转换到中心位置，可以通过shift变换来实现。

4.1 Numpy实现傅里叶逆变换

　　下面介绍 Numpy实现傅里叶逆变换，它是傅里叶变换的逆操作，将频谱图像转换为原始图像的过程。通过傅里叶变换将转换为频谱图，并对高频（边界）和低频（细节）部分进行处理，接着需要通过傅里叶逆变换恢复为原始效果图。频域上对图像的处理会反映在逆变换图像上，从而更好地进行图像处理。

　　图像傅里叶变换主要使用的函数如下所示：

#实现图像逆傅里叶变换，返回一个复数数组
numpy.fft.ifft2(a, n=None, axis=-1, norm=None)

#fftshit()函数的逆函数，它将频谱图像的中心低频部分移动至左上角
numpy.fft.fftshift()

#将复数转换为0至255范围
iimg = numpy.abs(逆傅里叶变换结果)

 　　下面代码实现了傅里叶变换和傅里叶逆变换

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 读取图像
img = cv2.imread('irving.jpg', )
# 图像进行灰度化处理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅里叶变换
# 快速傅里叶变换算法得到频率分布
f = np.fft.fft2(img)
# 默认结果中心点位置是在左上角 调用fftshift()函数转移到中间位置
fshift = np.fft.fftshift(f)
# fft 结果是复数，其绝对值结果是振幅
rimg = np.log(np.abs(fshift))

# 傅里叶逆变换
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)


# 展示结果
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('original Fourier')
plt.axis('off')
plt.subplot(132), plt.imshow(rimg, 'gray'), plt.title('fourier Fourier')
plt.axis('off')
plt.subplot(133), plt.imshow(iimg, 'gray'), plt.title('inverse fourier Fourier')
plt.axis('off')
plt.show()

　　结果如下：

4.2 OpenCV实现傅里叶逆变换

　　在OpenCV中，通过函数 cv2.idft()函数实现傅里叶逆变换，其返回结果取决于原始图像的类型和大小，原始图像可以为复数或实数，同时也要注意输入图像需要先转换成 np.float32格式，其函数原型如下：

dst = cv2.idft(src[, dst[, flags[, nonzeroRows]]])

 　　参数意义：

• src表示输入图像，包括实数或复数
• dst表示输出图像
• flags表示转换标记
• nonzeroRows表示要处理的dst行数，其余行的内容未定义（请参阅dft描述中的卷积示例）

 　　完整代码如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
from matplotlib import pyplot as plt

# 读取图像
img = cv2.imread('irving.jpg', )
# 图像进行灰度化处理
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 傅里叶变换
# cv2.DFT_COMPLEX_OUTPUT 执行一维或二维复数阵列的逆变换，结果通常是相同大小的复数数组
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 将频谱低频从左上角移动到中心位置
dft_shift = np.fft.fftshift(dft)
# 频谱图像双通道复数转换为0~255区间
result = 10 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

# 傅里叶逆变换
ishift = np.fft.ifftshift(dft_shift)
iimg = cv2.idft(ishift)
iresult = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])


# 显示图像
plt.subplot(131), plt.imshow(img, cmap='gray')
plt.title('Input image')
plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(result, cmap='gray')
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(iresult, cmap='gray')
plt.title('inverse Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()

 　　结果如图所示：

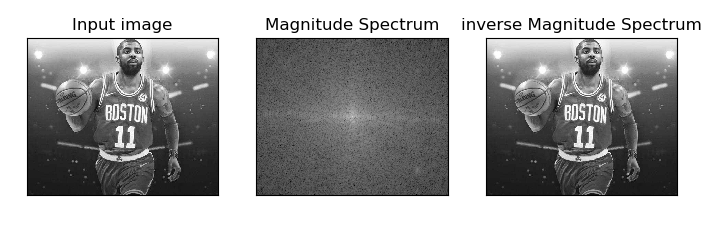
 　　傅里叶变换的目的并不是为了观察图像的频率分布（至少不是最终目的），更多情况下是为了对频率进行过滤，通过修改频率以达到图像增强，图像去噪，边缘检测，特征提取，压缩加密等目的。

　　过滤的方法一般有三种：低通（low-pass），高通（high-pass），带通（band-pass），下面一一学习。

5，高通滤波

　　高通滤波器是指通过高频的滤波器，衰减低频而通过高频，常用于增强尖锐的细节，但会导致图像的对比度会降低。该滤波器将检测图像的某个区域，根据像素与周围像素的差值来提升像素的亮度。下图展示了“Lena”图对应的频谱图像，其中心区域为低频部分。

　　接着通过高通滤波器覆盖掉中心低频部分，将255的点变换为0，同时保留高频部分，其处理过程如下图所示：

　　高通滤波器主要通过矩阵设置构造，其核心代码如下：

rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

　　下面自己百度找一张lena图，做一下，代码如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv2.imread('lena.jpg', 0)

# 傅里叶变换
fimg = np.fft.fft2(img)
fshift = np.fft.fftshift(fimg)

# 设置高通滤波器
rows, cols = img.shape
crow, ccol = int(rows/2), int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

# 傅里叶逆变换
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)

# 显示原始图像和高通滤波处理图像
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('gray Image')
plt.axis('off')
plt.subplot(122), plt.imshow(iimg, 'gray'), plt.title('Result Image')
plt.axis('off')
plt.show()

 　　结果如下：

 　　左边图为lena的灰度图，右边图为高通滤波器提取的边缘轮廓图像，它通过傅里叶变换转换为频谱图像，再将中心的低频部分设置为0，再通过傅里叶逆变换转换为最终输出图像。

6，低通滤波

　　所谓低通就是保留图像中的低频成分，过滤高频成分，可以把过滤器想象成一张渔网，想要低通过滤器，就是要将高频区域的信号全部拉黑，而低频区域全部保留。例如，在一幅大草原的图像中，低频对应着广袤且颜色趋于一致的草原，表示图像变换缓慢的灰度分量；高频对应着草原图像中的老虎等边缘信息，表示图像变换较快的灰度分量，由于灰度尖锐过度造成。

　　低通滤波器是指通过低频的滤波器，衰减高频而通过低频，常用于模糊图像。低频滤波器与高通滤波器相反，当一个像素与周围像素的插值小于一个特定值时，平滑该像素的亮度，常用于去噪和模糊化处理。如PS软件中的高斯模糊，就是常见的模糊滤波器之一，属于削弱高频信号的低通滤波器。

　　下图展示了lena图对应的频谱图像，其中心区域为低频部分。如果构造低通滤波器，则将频谱图像中心低频部分保留，其他部分替换为黑色0，其处理过程如图所示，最终得到的效果图为模糊图像。

　　那么，如何构造该滤波图像呢？如下图所示，滤波图像是通过低通滤波器和频谱图像形成。其中低通滤波器中心区域为白色255，其他区域为黑色0。

　　低通滤波器主要通过矩阵设置构造，其核心代码如下：

rows, cols = img.shape
crow,ccol = int(rows/2), int(cols/2)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

 　　通过低通滤波器将模糊图像的完整代码如下：

# _*_ coding:utf-8 _*_
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
img = cv2.imread('lena.jpg', 0)

# 傅里叶变换
# fimg = np.fft.fft2(img)
fimg = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
fshift = np.fft.fftshift(fimg)

# 设置低通滤波器
rows, cols = img.shape
# 中心位置
crow, ccol = int(rows / 2), int(cols / 2)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

# 掩膜图像和频谱图像乘积
f = fshift * mask
print(f.shape, fshift.shape, mask.shape)
# (199, 198, 2) (199, 198, 2) (199, 198, 2)


# 傅里叶逆变换
ishift = np.fft.ifftshift(f)
iimg = cv2.idft(ishift)
iimg = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])

# 显示原始图像和高通滤波处理图像
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('gray Image')
plt.axis('off')
plt.subplot(122), plt.imshow(iimg, 'gray'), plt.title('Result Image')
plt.axis('off')
plt.show()

　　结果如下：

 

 

 

 

参考文献：https://blog.csdn.net/Eastmount/article/details/89474405

https://blog.csdn.net/Eastmount/article/details/89645301

Python + OpenCV图像处理课程（https://study.163.com/course/courseLearn.htm?courseId=1005317018#/learn/text?lessonId=1052508042&courseId=1005317018）

https://www.cnblogs.com/tenderwx/p/5245859.html

https://blog.csdn.net/u013921430/article/details/79934162?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param