python常用算法(7)——动态规划,回溯法
完整代码及其数据,请移步小编的GitHub
传送门:请点击我
如果点击有误:https://github.com/LeBron-Jian/BasicAlgorithmPractice
引言:从斐波那契数列看动态规划
斐波那契数列:Fn = Fn-1 + Fn-2 ( n = 1,2 fib(1) = fib(2) = 1)
练习:使用递归和非递归的方法来求解斐波那契数列的第 n 项
代码如下:
# _*_coding:utf-8_*_
def fibnacci(n):
if n == 1 or n == 2:
return 1
else:
return fibnacci(n - 1) + fibnacci(n - 2)
# 写这个是我们会发现计算f(5) 要算两边f(4)
# f(5) = f(4)+f(3)
# f(4) = f(3)+f(2)
# f(3) = f(2)+f(1)
# f(3) = f(2)+f(1)
# f(2) = 1
# 那么同理,算f(6),我们会计算两次f(5),三次f(4)....
# 当然不是说所有的递归都会重复计算,
# 时间随着数字越大,时间越长
print(fibnacci(10)) # 55
简单来说,就是想要计算f(5),我们需要先计算出子问题 f(4) 和 f(3),然后要计算 f(4) ,我们需要先计算出子问题 f(3) 和 f(2),以此类推,最后遇到 f(1) 或者 f(2) 的时候,结果已知,就能直接返回结果,递归树不再向下生长了。
递归算法的时间复杂度怎么计算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为 O(2^n),指数级别,爆炸。
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,比如 f(5) 被计算了两次,而且你可以看到,以 f(5) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。更何况,还不止 f(5) 这一个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第一个性质:重叠子问题。下面,我们想办法解决这个问题。
明确了问题,其实就已经把问题解决了一半。即然耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
def fibnacci_n_recurision(n):
f = [0, 1, 1]
if n > 2:
for i in range(n - 2):
num = f[-1] + f[-2]
f.append(num)
return f[n]
print(fibnacci_n_recurision(10))
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
递归算法的时间复杂度怎么算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 f(1), f(2), f(3) ... f(20),数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
至此,带备忘录的递归解法的效率已经和动态规划一样了。实际上,这种解法和动态规划的思想已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
啥叫「自顶向下」? 就是从上向下延伸,都是从一个规模较大的原问题比如说 f(5),向下逐渐分解规模,直到 f(1) 和 f(2) 触底,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(5),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
为了让我们的说服更有理一些,这里写了一个装饰器,我们通过运行时间看。同样对于上面两个函数,一个递归,一个非递归,我们输入 n=15
# cal_time.py 函数代码如下:
import time
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*arg, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
运行结果:
fibnacci running time: 0.01000070571899414 secs.
fibnacci_n_recurision running time: 0.0 secs.
总结来说,就是递归非常非常的慢,那非递归相对来说就比较快了。那为什么呢?就是为什么递归的效率低。我们上面代码也说过了,就是对子问题进行重复计算了。那第二个函数为什么快呢,我们将每次的计算结果存在了函数里,直接调用,避免了重复计算(当然不是说所有的递归都会重复计算子问题),第二个函数我们其实可以看做是动态规划的思想,从上面的代码来看:
动态规划的思想==递推式+重复子问题
怎么理解呢,就是说动态规划遵循一套固定的流程:递归的暴力解法 ——> 带备忘录的递归解法 ——> 非递归的动态规划解法 这个过程是层次递进的解决问题的过程,你如果没有前面的铺垫,直接看最终的非递归动态规划解法,当然觉得难。
1,什么是动态规划
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
1.1,使用动态规划特征
- 1. 求一个问题的最优解
- 2. 大问题可以分解为子问题,子问题还有重叠的更小的子问题
- 3. 整体问题最优解取决于子问题的最优解(状态转移方程)
- 4. 从上往下分析问题,从下往上解决问题
- 5. 讨论底层的边界问题
1.2,动态规划的基本思想
若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有效。
动态规划最重要的有三个概念:1、最优子结构 2、边界 3、状态转移方程
所以我们在学习动态规划要明白三件事情:
1,目标问题
2,状态的定义:opt[n]
3,状态转移方程:opt[n] = best_of(opt[n-1], opt[n-2])
其实状态转移方差直接代表着暴力解法,千万不要看不起暴力解,动态规划问题最难的就是写出状态转移方差,即这个暴力解。
2,钢条切割问题
某公司出售钢条,出售价格与钢条长度直接的关系如下表:

问题:现在有一条长度为 n 的钢条和上面的价格表,求切割钢条方案,使得总收益最大。
分析:长度为4的钢条的所有切割方案如下:(C方案最优)
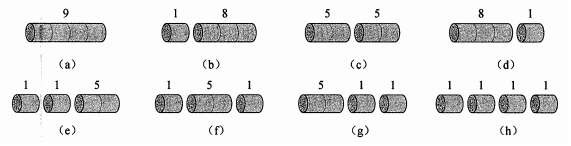
思考:长度为 n 的钢条的不同切割方案有几种?
下面是当长度为n的时候,最优价格的表格( i 表示长度为 n ,r[i] 表示最优价格)
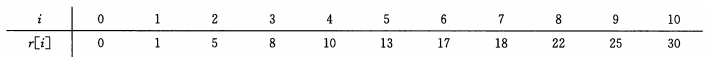
2.1,递推式解决钢条切割问题
设长度为 n 的钢条切割后最优收益值为 Rn,可以得到递推式:

第一个参数Pn 表示不切割
其他 n-1个参数分别表示另外 n-1种不同切割方案,对方案 i=1,2,...n-1 将钢条切割为长度为 i 和 n-i 两段
方案 i 的收益为切割两段的最优收益之和,考察所有的 i,选择其中收益最大的方案
2.2,最优子结构解决钢条切割问题
可以将求解规模为 n 的原问题,划分为规模更小的子问题:完成一次切割后,可以将产生的两段钢条看成两个独立的钢条切割问题。
组合两个子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大的,构成原问题的最优解。
钢条切割满足最优子结构:问题的最优解由相关子问题的最优解组合而成,这些子问题可以独立求解。
钢条切割问题还存在更简单的递归求解方法:
- 从钢条的左边切割下长度为 i 的一段,只对右边剩下的一段继续进行切割,左边的不再切割
- 递推式简化为:

- 不做切割的方案就可以描述为:左边一段长度为 n,收益为 pn,剩下一段长度为0,收益为 r0=0.
2.3,钢条切割问题——自顶向下递归代码及其时间复杂度
代码如下:
def _cut_rod(p, n):
if n == 0:
return 0
q = 0
for i in range(1, n+1):
q = max(q, p[i] + _cut_rod(p, n-i))
return q
如下图所示,当钢条的长度增加时候,切割的方案次数随着指数增加。当n=1的时候切割1次,n=2的时候切割2次,n=3的时候切割4次,n=4的时候切割8次。。。。
所以:自顶向下递归实现的时间复杂度为 O(2n)
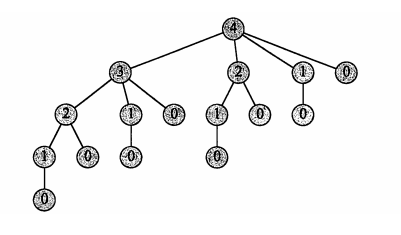
2.4,两种方法的代码实现
代码如下:
# _*_coding:utf-8_*_
import time
# 给递归函数一个装饰器,它就递归的装饰!! 所以为了防止这样我们再套一层即可
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print('%s running time : %s secs' % (func.__name__, t2 - t1))
return result
return wrapper
# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 28, 30, 33, 36, 39, 40]
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
def cut_rod_recurision_1(p, n):
if n == 0:
return 0
else:
res = p[n]
for i in range(1, n):
res = max(res, cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n - i))
return res
# print(cut_rod_recurision_1(p, 9))
def cut_rod_recurision_2(p, n):
if n == 0:
return 0
else:
res = 0
for i in range(1, n + 1):
res = max(res, p[i] + cut_rod_recurision_2(p, n - i))
return res
# print(cut_rod_recurision_2(p, 9))
@cal_time
def c1(p, n):
return cut_rod_recurision_1(p, n)
@cal_time
def c2(p, n):
return cut_rod_recurision_2(p, n)
print(c1(p, 10))
print(c2(p, 10))
'''
c1 running time : 0.02000117301940918 secs
30
c2 running time : 0.0010001659393310547 secs
30
'''
我们通过计算时间,发现第二个递归方法明显比第一个递归方法快很多。那么是否还有更简单的方法呢?肯定有,下面学习动态规划。
2.5,动态规划解决钢条切割问题
递归算法由于重复求解相同子问题,效率极低。即使优化过后的递归也效率不高。那这里使用动态规划。
动态规划的思想:
- 每个子问题只求解一次,保存求解结果
- 之后需要此问题时,只需要查找保存的结果
动态规划解法代码:
def cut_rod_dp(p, n):
r = [0 for _ in range(n+1)]
for j in range(1, n+1):
q = 0
for i in range(1, j+1):
q = max(q, p[i]+r[j-i])
r[j] = q
return r[n]
或者便于理解这样:
def cut_rod_dp(p, n):
r = [0]
for i in range(1, n+1):
res = 0
for j in range(1, i+1):
res = max(res, p[j]+r[i-j])
r.append(res)
return r[n]
时间复杂度: O(n2)

2.6,钢条切割问题——重构解
如何修改动态规划算法,使其不仅输出最优解,还输出最优切割方案?
对于每个子问题,保存切割一次时左边切下的长度

下图为r[i] 表示最优切割的价格,s[i]表示切割左边的长度。

代码如下:
def cut_rod_extend(p, n):
r = [0]
s = [0]
# 这个循环的意思是从底向上计算
for i in range(1, n+1):
res_r = 0 # 用来记录价格的最优值
res_s = 0 # 用来记录切割左边的最优长度
for j in range(1, i+1):
if p[j] + r[i-j] > res_r:
res_r = p[j] + r[i-j]
res_s = j
r.append(res_r)
s.append(res_s)
return r[n], s
def cut_rod_solution(p, n):
r, s = cut_rod_extend(p, n)
ans = []
while n>0:
ans.append(s[n])
n-= s[n]
return ans
print(cut_rod_extend(p, 10))
# (30, [0, 1, 2, 3, 2, 2, 6, 1, 2, 3, 10])
print(cut_rod_solution(p, 9))
# [3, 6]
2.7,什么问题可以使用动态规划方法?
1,最优子结构
- 原问题的最优解中涉及多少个子问题
- 在确定最优解使用那些子问题时,需要考虑多少种选择
2,重叠子问题
3,最长公共子序列
一个序列的子序列是在该序列中删去若干元素后得到的序列。例如:ABCD 和 BDF 都是 ABCDEFG 的子序列。
在一个序列中,子串是连续的,子序列可以不连续。
最常公共子序列(LCS)问题:给定两个序列 X 和 Y,求 X 和 Y 长度最大的公共子序列。例如 X = ABBCBDE, Y = DBBCDB , LCS(X, Y) = BBCD 。
应用场景:字符串相似度比对。
3.1,最长公共子序列的思路——暴力穷举法
当X的长度为m,Y的长度为n,则时间复杂度为: 2^(m+n)
虽然我们最先想到的时暴力穷举法,但是很显然,由其时间复杂度可知,这是不可取的。
3.2,最长公共子序列的思路——LCS是否具有最优子结构性质

例如:要求 a = ABCBDAB 与 b = BDCABA 的LCS:
由于最后一位 B!= A
因此LCS(a, b)应该来源于 LCS(a[: -1], b)与 LCS(a, b[: -1]) 中更大的哪一个。
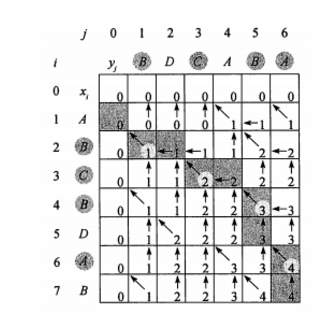
最优解的递推式如下:

c[i,j] 表示 Xi 和 Yj 的LCS 长度。
3.3,最长公共子序列的代码
代码如下:
def lcs_length(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]: # i,j位置上的字符匹配的时候,来自于左上方
c[i][j] = c[i - 1][j - 1] + 1
else:
c[i][j] = max(c[i - 1][j], c[i][j - 1])
# 逐行打印
for _ in c:
print(_)
return c[m][n]
# 最优值出来了,但是过程没有出来,也就是只有最长,不知道公共子序列
# print(lcs_length("ABCBDAB", "BDCABA"))
'''
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
4
'''
def lcs(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
# 1左上方 2上方 3 左方
b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]: # i,j位置上的字符匹配的时候,来自于左上方
c[i][j] = c[i - 1][j - 1] + 1
b[i][j] = 1
elif c[i - 1][j] > c[i][j - 1]: # 来自于上方
c[i][j] = c[i - 1][j]
b[i][j] = 2
else:
c[i][j] = c[i][j - 1]
b[i][j] = 3
return c[m][n], b
# c, b = lcs("ABCBDAB", "BDCABA")
# for _ in b:
# print(_)
'''
[0, 0, 0, 0, 0, 0, 0]
[0, 3, 3, 3, 1, 3, 1]
[0, 1, 3, 3, 3, 1, 3]
[0, 2, 3, 1, 3, 3, 3]
[0, 1, 3, 2, 3, 1, 3]
[0, 2, 1, 3, 3, 2, 3]
[0, 2, 2, 3, 1, 3, 1]
[0, 1, 2, 3, 2, 1, 3]
'''
def lcs_trackback(x, y):
c, b = lcs(x, y)
i = len(x)
j = len(y)
res = []
while i > 0 and j > 0:
if b[i][j] == 1: # 来自左上方 =》匹配
res.append(x[i - 1])
i -= 1
j -= 1
elif b[i][j] == 2: # 来自上方=》 不匹配
i -= 1
else: # ==3 来自左方 =》不匹配
j -= 1
# 因为是回溯法,所以倒着写的,我们最后需要reverse回来
return "".join(reversed(res))
print(lcs_trackback("ABCBDAB", "BDCABA"))
# BDAB
4,最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大值。
示例:输入:[-2, 1, -3, 4, -1, 2, 1, -5, 4] 输出:输出:6
思路:我们首先分析题目,为什么最大和的连续子数组不包括其他的元素而是这几个呢?如果我们想在现有的基础上去扩展当前连续子数组,相邻的元素是一定要被加入的,而相邻元素可能会减损当前的和。
4.1,遍历法
算法过程:遍历数组,用 sum 去维护当前元素加起来的和,当 sum 出现小于0的情况时,我们把它设为0,然后每次都更新全局最大值。
def maxSubArray(self, nums: List[int]) -> int:
sum = 0
MaxSum = nums[0]
for i in range(len(nums)):
sum += nums[i]
MaxSum = max(sum, MaxSum)
if sum <0:
sum = 0
return MaxSum
那看起来这么简单,如何理解呢?一开始思考数组是个空的,我们每次选一个 nums[i] 加入当前数组中新增了一个元素,也就是用动态的眼光去考虑。代码简单为什么就能达到效果呢?
我们进行的加和是按照顺序来的,当我们i 选出来后,加入当前 sum,这时候有两种情况:
1,假设我们当前 sum 一致都大于零,那每一次计算的 sum 都是包括开头元素的一端子序列。
2,出现小于0的时候,说明我们当前子序列第一次小于零,所以我们现在形成的连续数组不能包括之前的连续子序了,于是抛弃他们,重新开始新的子序。
4.2,动态规划
设sum[i]为以第i个元素结尾的最大的连续子数组的和。假设对于元素i,所有以它前面的元素结尾的子数组的长度都已经求得,那么以第i个元素结尾且和最大的连续子数组实际上,要么是以第i-1个元素结尾且和最大的连续子数组加上这个元素,要么是只包含第i个元素,即sum[i]= max(sum[i-1] + a[i], a[i])。可以通过判断sum[i-1] + a[i]是否大于a[i]来做选择,而这实际上等价于判断sum[i-1]是否大于0。由于每次运算只需要前一次的结果,因此并不需要像普通的动态规划那样保留之前所有的计算结果,只需要保留上一次的即可,因此算法的时间和空间复杂度都很小。
代码如下:
def maxSubArray4(self, nums: List[int]) -> int:
length = len(nums)
for i in range(1, length):
# 当前值的大小与前面的值之和比较,若当前值更大,则取当前值,舍弃前面的值之和
subMaxSum = max(nums[i]+nums[i-1], nums[i])
# 将当前和最大的赋给 nums[i], 新的nums 存储的为何值
nums[i] = subMaxSum
return max(nums)
只要遍历一遍。nums[i]表示的是以当前这第i号元素结尾(看清了一定要包含当前的这个i)的话,最大的值无非就是看以i-1结尾的最大和的子序能不能加上我这个nums[i],如果nums[i]>0的话,则加上。注意我代码中没有显式地去这样判断,不过我的Max表达的就是这个意思,然后我们把nums[i]确定下来。
4.3 总结
计算机解决问题其实没有任何奇技淫巧,它唯一的解决办法就是穷举,穷举所有可能性。算法设计无法就是先思考“如何穷举”,然后再追求“如何聪明的穷举”。
列出动态转移方差,就是在解决“如何穷举”的问题,之所以说他难,一是因为很多穷举需要递归实现,二是因为有的问题本身的解空间复杂,不难容易穷举完整。
备忘录,DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路,是降低时间复杂度的不二法门。
动态规划需要和回溯法搭配着使用,动态规划只负责求最优解,而回溯法则可以找到最优值的路径。
5,回溯法
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为 “回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。回溯法有“通用的解题法”之称,也叫试探法,它是一种系统的搜索问题的解的方法。简单来说,回溯法采用试错的方法解决问题,一旦发现当前步骤失败,回溯方法就返回上一个步骤,选择另一种方案继续试错。
5.1 回溯法的基本思想
从一条路往前走,能进则进,不能进则退回来,换一条路再试。
5.2 回溯法的一般步骤
1,定义一个解空间(子集树,排序树二选一)
2,利用适用于搜索的方法组织解空间
3,利用深度优先法搜索解空间
4,利用剪枝函数避免移动到不可能产生解的子空间
5.3 回溯法针对问题的特点
回溯算法针对的大多数问题有以下特点:问题的答案有多个元素(可向下成走迷宫是有多个决定),答案需要一些约束(比如数独),寻找答案的方式在每一个步骤相同。回溯算法逐步构建答案,并在确定候选元素不满足约束后立刻放弃候选元素(一旦碰墙就返回),直到找到答案的所有元素。
5.4回溯法题目——查找单词
问题描述:你玩过报纸上那种查找单词的游戏吗?就是那种在一堆字母中横向或竖向找出单词的游戏。小明在玩一个和那个很像的游戏,只不过现在不仅可以上下左右连接字母,还可以拐弯。如图所示,输入world,就会输出“找到了”。
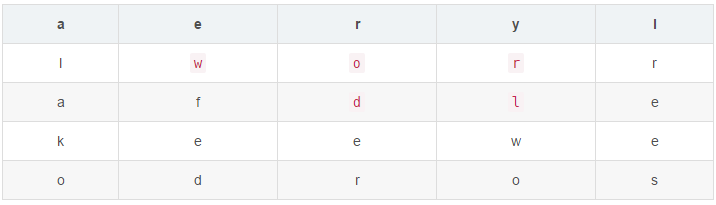
5.5 回溯法题目——遍历所有的排列方式
问题描述:小米最近有四本想读的书:《红色的北京》,《黄色的巴黎》,《蓝色的夏威夷》,《绿色的哈萨里》,如果小明每次只能从图书馆借一本书,他一共有多少种借书的顺序呢?
回溯法是一种通过探索所有可能的候选解来找出所欲的解的算法。如果候选解被确认,不是一个解的话(或者至少不是最后一个解),回溯算法会通过在上一步进行一些变换排期该解。即回溯并且再次尝试。
这里有一个回溯函数,使用第一个整数的索引作为参数 backtrack(first)。
1,如果第一个整数有索引 n,意味着当前排列已完成。
2,遍历索引 first 到索引 n-1 的所有整数 ,则:
- 在排列中放置第 i 个整数,即 swap(nums[first], nums[i])
- 继续生成从第 i 个整数开始的所有排列:backtrack(first +1)
- 现在回溯,通过 swap(nums[first], nums[i]) 还原。
代码如下:
class Solution:
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def backtrack(first = 0):
# if all integers are used up
if first == n:
output.append(nums[:])
for i in range(first, n):
# place i-th integer first
# in the current permutation
nums[first], nums[i] = nums[i], nums[first]
# use next integers to complete the permutations
backtrack(first + 1)
# backtrack
nums[first], nums[i] = nums[i], nums[first]
n = len(nums)
output = []
backtrack()
return output
便于理解的代码如下:
class solution:
def solvepermutation(self, array):
self.helper(array, [])
def helper(self, array, solution):
if len(array) == 0:
print(solution)
return
for i in range(len(array)):
newarray = array[:i] + array[i + 1:] # 删除书本
newsolution = solution + [array[i]] # 加入新书
self.helper(newarray, newsolution) # 寻找剩余对象的排列组合
solution().solvepermutation(["红", "黄", "蓝", "绿"])
方法二:走捷径(直接使用Python的库函数,迭代函数itertools)
li = ['A', 'B', 'C', 'D']
def solutoin(li):
import itertools
res = list(itertools.permutations(li))
return len(res)
5.6 回溯法问题——经典问题的组合
问题描述:小明想上两门选修课,他有四种选择:A微积分,B音乐,C烹饪,D设计,小明一共有多少种不同的选课组合?
当然第一个方法就是走捷径!,直接使用python的库函数itertools进行迭代:
li = ['A', 'B', 'C', 'D']
def solutoin(li):
import itertools
res = list(itertools.permutations(li, 2))
return len(res)
下面开始回溯法的学习。
class solution():
def solvecombination(self, array, n):
self.helper(array, n, [])
def helper(self, array, n, solution):
if len(solution) == n:
print(solution)
return
for i in range(len(array)):
newarray = array[i + 1:] # 创建新的课程列表,更新列表,即选过的课程不能再选
newsolution = solution + [array[i]] # 将科目加入新的列表组合
self.helper(newarray, n, newsolution)
solution().solvecombination(["A", "B", "C", "D"], 2)
5.7 回溯法问题——八皇后问题
问题描述:保安负责人小安面临一个难题,他需要在一个8x8公里的区域里修建8个保安站点,并确保每一行、每一列和每一条斜线上都只有一个保安站点。苦恼的小安试着尝试布置了很多遍,但每一次都不符合要求。小安求助程序员小明,没过多久小明就把好几个布置方案(实际上,这个问题有92种答案)发给了小安,其中包括下面执行结果截图,试问小明是怎么做到的。
6,算法综合作业
这是所有的算法学完后的综合作业,当然这也是算法学习的一个总结。当然下面的问题我都有涉及,这里不做一一解答。
1. 实现以下算法并且编写解题报告,解题报告中需要给出题目说明、自己对 题目的理解、解题思路、对算法的说明和理解、以及算法复杂度分析等内容 2. 实现冒泡排序、插入排序、快速排序和归并排序 3. 以尽可能多的方法解决2-sum问题并分析其时间复杂度:给定一个列表和 一个整数,从列表中找到两个数,使得两数之和等于给定的数,返回两个数 的下标。题目保证有且只有一组解 4. 封装一个双链表类,并实现双链表的创建、查找、插入和删除 5. 使用至少一种算法解决迷宫寻路问题 6. 使用动态规划算法实现最长公共子序列问题
参考分治与动态规划参考文献:https://blog.csdn.net/weixin_41250910/article/details/94502136
https://blog.csdn.net/weixin_43482259/article/details/97996658



