tensorflow学习笔记：卷积神经网络最终笔记

　　这已经是我的第五篇博客学习卷积神经网络了。之前的文章分别是：

　　1，Keras深度学习之卷积神经网络（CNN），这是开始学习Keras，了解到CNN，其实不懂的还是有点多，当然第一次笔记主要是给自己心中留下一个印象，知道什么是卷积神经网络，而且主要是学习Keras，顺便走一下CNN的过程。

　　2，深入学习卷积神经网络（CNN）的原理知识，这次是对CNN进行深入的学习，对其原理知识认真学习，明白了神经网络如何识别图像，知道了卷积如何运行，池化如何计算，常用的卷积神经网络都有哪些等等。

　　3，TensorFlow学习笔记——图像识别与卷积神经网络，这里开始对TensorFlow进行完整的学习，以CNN为基础开始对TensorFlow进行完整的学习，而这里练习的是 LeNet网络。

　　4，深入学习卷积神经网络中卷积层和池化层的意义，这篇是对卷积神经网络中卷积层和池化层意义的深入学习，用一个简单的例子，阐述了其原理。

　　今天构建两个完整卷积神经网络，一个简单的MNIST热个身，一个稍微复杂的Cifar，今天学习完，不再做基础的卷积神经网络的相关笔记，我相信自己已经掌握了。

　　卷积神经网络是目前深度学习技术领域中非常具有代表性的神经网络之一，在图像分析和处理领域取得了众多突破性的进展，在学术界常用的标准图像标注集ImageNet上，基于卷积神经网络取得了很多成就，包括图像特征提取分类，场景识别等。卷积神经网络相较于传统的图像处理算法的优点之一在于避免了对图像复杂的前期预处理过程，尤其是人工参与图像预处理过程，卷积神经网络可以直接输入原始图像进行一系列的工作，至今已经广泛应用于各类图像相关的应用中。

　　卷积神经网络（Convolutional Neural Network  CNN）最初是为解决图像识别等问题设计的，当然其现在的应用不仅限于图像和视频，也可用于时间序列信号，比如音频信号，文本数据等。在早期的图像识别研究中，最大的挑战是如何组织特征，因为图像数据不像其他类型的数据那样可以通过人工理解来提取特征。在股票预测等模型中，我们可以从原始数据中提取过往的交易价格波动，市盈率，市净率，盈利增长等金融因子，这既是特征工程。但是在图像中，我们很难根据人为理解提取出有效而丰富的特征。在深度学习出现之前，我们必须借助 SIFT，HoG等算法提取具有良好区分性的特征，再集合 SVM 等机器学习算法进行图像识别。如下图所示，SIFT对一定程度内的缩放，平移，旋转，视觉改变，亮度调整等畸变，都具有不变性，是当前最重要的图像特征提取方法之一。可以说在之前只能依靠SIFT等特征提取算法才能勉强进行可靠地图像识别。

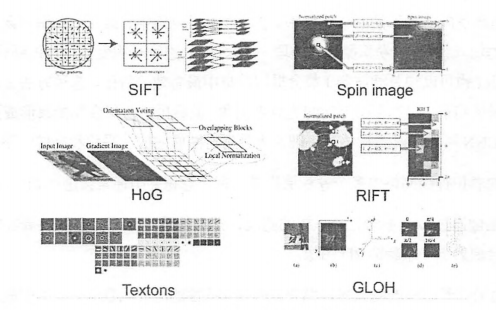
 　　然而SIFT这类算法提取的特征还是有局限性的，在ImageNet ILSVRC 比赛的最好结果的错误率也有26%以上，而且常年难以产生突破。卷积神经网络提取的特征则可以达到更好的效果，同时它不需要将特征提取和分类训练两个过程分开，它在训练时就自动提取了最有效的特征。CNN作为一个深度学习架构被提出的最初诉求，是降低对图像数据预处理的要求，以及避免复杂的特征工程。CNN可以直接使用图像的原始像素作为输入，而不必使用SIFT等算法提取特征，减轻了使用传统算法如SVM时必须做的大量重复，繁琐的数据预处理工作。和SITF等算法类似，CNN的最大特点在于卷积的权值共享结构，可以大幅减少神经网络的参数量，防止过拟合的同时又降低了神经网络模型的复杂度。CNN的权重共享其实也很像早期的延时神经网络（TDNN），只不过后者是在时间这一个维度上进行权值共享，降低了学习时间序列信号的复杂度。

1，CNN在图像分类问题上有什么优势？

　　这里使用水果分类来分析一下SVM以及神经网络的劣势。

　　如果我们有一组水果的图片，里面有草莓，香蕉和橘子。在图片尺寸较大的情况下，使用SVM分类的步骤是：

• 人工提取特征，比如说大小，形状，重量，颜色等。
• 根据上述特征，把每一张图片映射到空间中的一个点，空间的维度和特征的数量相等。
• 相同类别的物体具有类似的特征，所以空间中标记为草莓的点肯定是聚在一起的，香蕉和橘子也是同理。这时候使用SVM算法在空间中画出各类点之间的分界线就完成了分类。

　　在最后一步中，不使用SVM，使用别的分类器也是可以的，比如KNN，贝叶斯，甚至神经网络都是可以的。虽然不同算法中性能会有差异，但是这里我想说的就是在图像分类问题上的瓶颈并不在算法的性能上，而是在特征的提取上。

　　区分草莓和橘子的特征是容易提取的，那橘子和橙子呢？如果上述四个特征不能很好的区分橘子和橙子，想要进一步提升算法的性能怎么办？通常的做法是需要提取新的特征。那么新的特征如何选择呢？对于我这种水果盲来说，这个问题是具有一定难度的。

　　除了橘子橙子问题，我们还有猫狗如何区分，狗品种如何识别等一系列问题。我想对于大部分人来说，狗狗品种的识别是非常有难度的。转了一圈回来，突然发现，图像分类任务的瓶颈惊人出现在特征选择上。

　　如果我们用神经网络直接对猫狗进行分类呢？这样不就避开了特征提取这一步了啊？假设输入图片大小为30*30，那么设置900个输入神经元，隐含层设置1000个神经元，输出神经元个数对应需要的输出数量不就好了吗？甚至用SVM也可以这样做，把一张30*30的图看做900维空间中的一个点，代表猫的点和代表狗的点在这个900维的空间中必然是相聚于两个簇，然后我们就可以使用SVM来划出分界线了。

　　但是这样计算开销就太大了，对于30*30的图片我们也许可以这样做，对于1000*1000的图片我们这样做的话就需要至少一百万个隐层神经元，这样我们就至少更新10^12个参数。而SVM的话，则相当于在一百万维的空间中运行了。运行量将会大的难以估计。另外图中并不是所有的信息都和我们需要的。背景对我们的分类毫无价值，然而在这种一股脑全部拿来做输入的情况下，背景也被当成了特征进入了模型当中，准确度自然会有所下降。

　　总之，如果不人工提取特征，那么计算量会非常大，精确度也无法保证。而人工提取特征的方式又会在某些问题下难以进行，比如狗狗品种分类。

　　而CNN通过它独有的方式，成功的解决了这两个问题。也就是说，CNN是一个可以自动提取特征而却待训练参数相对不那么多的神经网络，这就是CNN在图像分类任务中决定性的优势。

2，为什么要使用卷积层？

　　和神经网络模型类似，CNN的设计灵感同样来自于对神经细胞的研究。

    1981 年的诺贝尔医学奖，颁发给了 David Hubel、TorstenWiesel，以及 
Roger Sperry。他们的主要贡献，是发现了人的视觉系统的信息处理是分级的。

    从低级的V1区提取边缘特征，再到V2区的形状或者目标的部分等，再到更高层，
整个目标、目标的行为等。也就是说高层的特征是低层特征的组合，从低层到高层
的特征表示越来越抽象，越来越能表现语义或者意图。而抽象层面越高，存在的可
能猜测就越少，就越利于分类。

　　值得一提的是，最低级的V1区需要提取边缘特征，而在上面提到的分类中，神经网络实际上是把30 * 30 的图片按照 900 个像素点处理的，那么有没有一种方法能够神经网络像人一样，按照边缘来理解呢？

　　卷积计算并不复杂，矩阵对应元素相乘的和就是卷积的结果，到了神经网络中会多出偏置b还有激活函数，具体方法如下图：

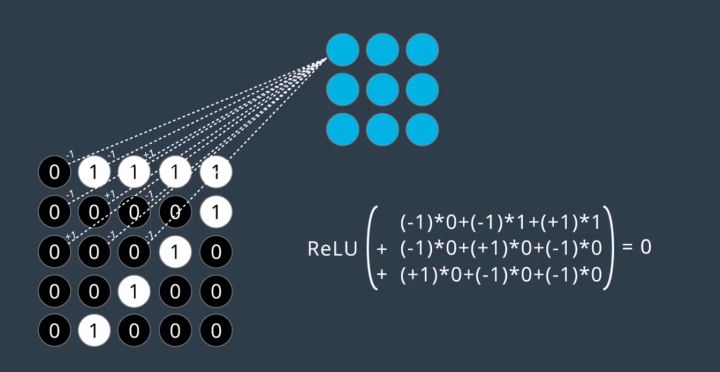
　　图片中展示的是由九个权重组成的矩阵和图片上九个像素点组成矩阵进行卷积过程。在偏置b为0，激活函数使用ReLU的情况下，过程就像图片右下角的公式一样，对应元素乘积的和，再加上值为0的b，然后外套激活函数得到输出0。

　　你可能会想到这部分的计算和普通的神经网络没神经网络没什么差别，形式都是 f(wx + b)。那么这么处理和边缘有什么关系？多做几次卷积就知道了。

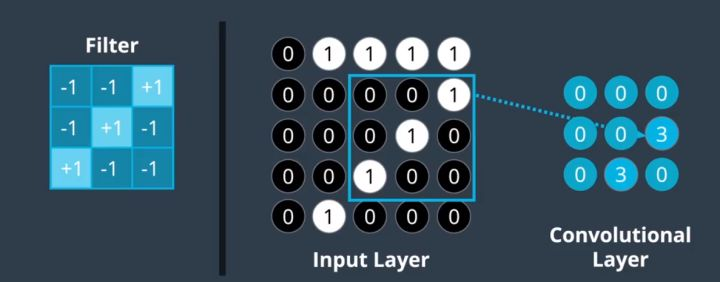
　　Filter 指的是权重组成矩阵，Input Layer中存的是图片中的全部像素。Convolutional Layer存的是Filter与图片中所有3*3矩阵依次卷积后得到的结果。在输出中我们可以看到两个3，他们比其他的元素0都要大。是什么决定了卷积结果的大小？观察后发现，图中参与卷积的部分1的排序和活动窗口中1的排列完全一样时，输出为3。而像素的排列方式其实就是图片中的形状，这说明如果图像中的形状和Filter中的形状相似的话，输出值就大，不像就小。因此，卷积的操作建立了神经网络与图像边缘的联系。

　　实际上CNN经过训练之后，Filter中就是图片的边缘，角落之类的特征。也即是说，卷积层是在自动提取图片中的特征。

　　除此之外，卷积还有一种局部连接的思想在里面。他对图片的处理方式是一块一块的，并不是所有像素值一起处理。因此可以极大地降低参数值的总量。这里我需要使用那张经典的图片来说明卷积层是如何降低参数总量的：

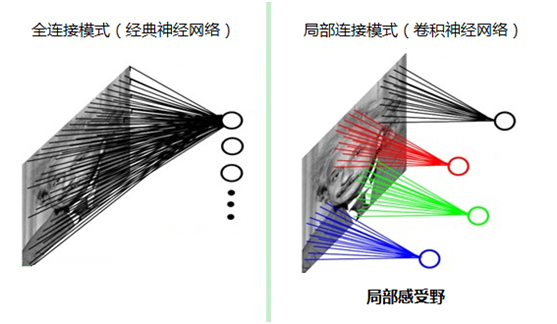
　　对于一张1000*1000的图片来说，对他进行分类，至少需要10的12次方个参数。而如果对图片使用卷积操作，每个神经元之和图像上的10*10的像素连接的话，参数总量就变成了10的8次方。但是这样的操作会导致一个问题，每个神经元只对图片一部分的内容，那么这个神经元学到的内容就不能应用到其他神经元上。比如说有这样一个训练集，同样自私的猫出现在黑色神经元负责的区域中，但是测试集中，猫可能出现在图片的任何位置。按照局部连接的做法，其他区域的猫是无法被正确识别的。

　　　而为了让出现在任何位置的猫都能够被正确的识别，提出了权重共享。让红绿蓝黑神经元中的参数全都一样，这样就可以使得模型的准确率不受物体位置的影响，看起来就像同一个Filter划过了整个图片。从提取特征的角度上来讲，一个Filter显然不能满足需求，因此需要生成多个不同的Filter来对图片进行卷积。更棒的是，为了获得平移不变性而使用的权重共享法，又以外的再一次降低了待训练参数总数。

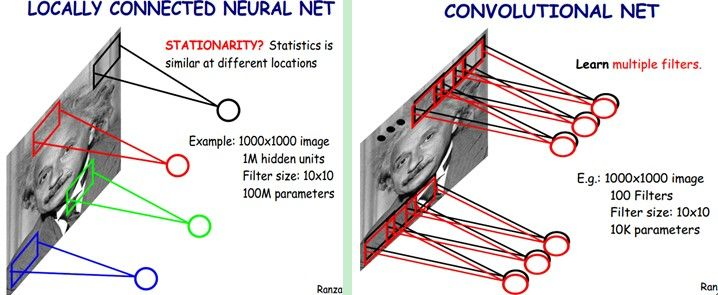
　　就是使用100个权值共享的10*10 Filter来卷积，总参数也才10的4次方。也就是说，参数相较于普通的神经网络而言，总共下降了整整8个数量级，这种提升是夸张的。

　　所以，卷积层的工作方式已经全部出来了，具体工作流程入下：

　　蓝色的部分代表输入图像；绿色的部分代表输出矩阵；周围的虚线是padding操作，可以看做图像的一部分；下方不断移动的阴影就是FIlter，其大小，数量，一次移动的距离都是可以自定义的；阴影至上方绿色的连线代表相乘再加之后的结果输出到了输出矩阵的那个位置。卷积层的折中操作方式，成功的模拟了生物视觉系统中的边缘特征提取部分。

　　而CNN中对于分级结构的模拟，是通过卷积层的层层叠加实现的。AlexNet的论文中不止一次的提到，网络的深度对CNN性能的影响是显著的。可以认为卷积层的不断叠加会使得提取到的特征越来越复杂，整个流程就像上述引用中提到的人类的视觉系统的工作方式一样运行，最终完成对图片的分类。

　　那么现在就可以很轻松的回答上面的问题了，使用卷积层是因为卷积层本质上是在自动提取图片的特征，而且在提取特征的同时，极大的降低了网络总体待训参数的总量。这两个特征使得CNN克服了特征提取困难，待训参数庞大的问题，成功制霸图片分类问题。

3，为什么要使用池化层？

 　　你可能会问，卷积层就已经把参数将了下来，还解决了特征提取的问题，那还加一个池化层干什么呢？（可能池化层只是工程上想让网络更深而做出的一个无奈之举）

　　就以最精彩出现的最大池化为例，来看看所谓的池化操作有多随便吧。

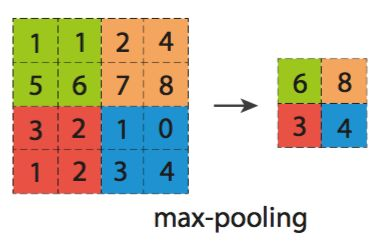
 　　一个2*2 的最大池化操作如上图，它做的就是把2*2窗口中的最大值存下来。所以绿色部分留下来了6；棕色部分是8；蓝色部分是4。所以就很简单，很随便，但是这个操作有什么优点呢？不知道，但是缺点却显而易见——损失了细节。为什么损失细节也要做这一步呢？可能就是要压缩矩阵，这样可以在模型中多加几层卷积层，用来提取更高维，更复杂的特征。而从压缩的角度来看，这一步可谓简单有效，一个取最大值的操作，就让矩阵大小变为四分之一。

　　AlexNet的出现时2012年，那时候用到的是GTX580，3G显存，文章中提到只用一块GPU是不行的，因为显存会爆，因此用了两块GPU并行进行这个任务。可能作者也是苦于总是爆显存，而不得不加上池化层。就算这样，还要用到两块GPU才成功训练了整个网络。

　　然而池化层的应用似乎带来更多的便利之处。由于其只取最大值，忽视掉了其他影响较小的值，所以在当内容发生很小的变化的时候包括一些平移旋转，CNN任然能够稳定识别对应内容。也就是说池化层给模型带来了一定程序上的不变性。

　　而应不应该使用池化层还是一个正在讨论的问题，有的网络用，有的网络不用。按照我的理解，在显存够用的情况下，不用池化层。这种丢失细节提升模型不变性的方法有点伤人伤己的意思。而且我们希望得到的模型并不是在不知道图片变化了的情况下可以得到正确结果，我们希望的是模型可以认识到差异却依然能做出正确的分类才对。

4，全连接层的作用

　　在经过几次卷积和池化的操作之后，卷积神经网络的最后一步是全连接层。这一步就和最最普通的神经网络没有什么区别。我认为这里的神经网络就是充当一个分类器的作用，输入时不同特征的特征值，输出的是分类。其实可以在训练好之后，把全连接层砍掉，把卷积部分的输出当做是特征，全连接层换成SVM或者别的分类器，重新训练，也是可以取得良好效果的。

5，总结

• 1，CNN之前的图片分类算法性能受制于特征的提取以及庞大参数数量导致的计算困难。
• 2，使用卷积来模拟人类视觉系统的工作方式，而这种方式极大的降低了神经网络的带训练参数数量。
• 3，为了获得平移不变形，使用了权重共享技术，该技术进一步降低了带训练参数数量
• 4，卷积层实际上是在自动提取图片特征，解决了图像特征提取这一难题。
• 5，使用池化层的根部原因是降低计算量，而其带来的不变形并不是我们需要的。不过在以模型准确率为纲的大背景下，继续使用无可厚非。
• 6，全连接层实质上是一个分类器。

6，卷积层的步骤

　　一般的卷积神经网络由多个卷积层构成，每个卷积层中通常会进行如下几个操作。

　　（1）图像通过多个不同的卷积核的滤波，并加偏置（bias），提取出局部特征，每一个卷积核会映射出一个新的2D图像。

　　（2）将前面卷积核的滤波输出结果，进行非线性的激活函数处理。目前最常见的是使用ReLU函数，而以前Sigmoid 函数用的比较多。

　　（3）对激活函数的结果再进行池化操作（即降采样，比如将 2*2 的图片降为 1*1 的图片），目前一般是使用最大池化，保留最显著的特征，并提升模型的畸变容忍能力。

　　这几个步骤就构成了最常见的卷积层，当然也可以加上一个 LRN（Local Response Normalization，局部响应归一化层）层，目前非常流畅的Trick 还有 Batch Normalization等。

七，卷积神经网络发展趋势

　　下面我们简单回顾卷积神经网络的历史，下图所示大致勾勒出最近几十年卷积神经网络的发展方向。Perceptron（感知机）于 1957年由 Frank Resenblatt 提出，而 Perceptron不仅是卷积网络，也是神经网络的始祖。Neocognitron（神经认知机）是一种多层级的神经网络，由日本科学家 Kunihiko Fukushima 于20世纪80年代提出，具有一定程度的视觉认知的功能，并直接启发了后来的卷积神经网络。LeNet-5 由 CNN之父 Yann LeCun 于 1997年提出，首次提到了多层级联的卷积结构，可对手写数字进行有效识别。可以看到前面这三次关于卷积神经网络的技术突破，间隔时间非常长，需要十余年甚至更久才出先一次理论创新。而后于2012年，Hinton的学生Alex依靠8层深的卷积神经网络一举获得了 ILSVRC 2012 比赛管局，瞬间点燃了卷积神经网络研究的热潮。AlexNet成功应用了 ReLU 激活函数，Dropout，最大覆盖池化，LRN层，CPU加速等新技术，并启发了后续更多的技术创新，卷积神经网络的研究从此进入快车道。

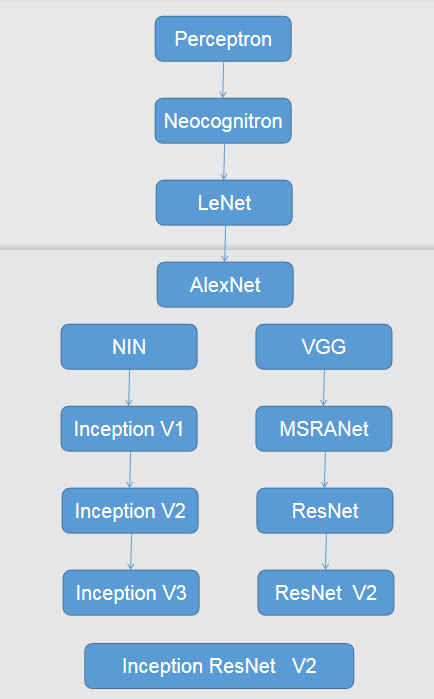
　　在AlexNet之后，我们可以将卷积神经网络的发展分为两类，一类是网络结构上的改进调整（上图的左侧分支），另一类是网络深度的增加（上图的右侧分支）。2013年，颜水成教授的 Network in Network 工作首次发布，优化了卷积神经网络的结构，并推广了 1*1 的卷积结构。在改进卷积网络结构的工作中，后继者还有2014年的Google Inception Net V1，提出了 Inception Module 这个可以反复堆叠的高效的卷积网络结构，并获得了当年 ILSVRC 比赛的冠军。2015年初的 inception V2提出了 Batch Normalization，大大加速了训练过程，并提升了网络性能。2015年年末的 Inception V3则继续优化了网络结构，提出来 Factorization in Small Convolutions 的思想，分解大尺寸卷积为多个小卷积乃至一维卷积。而另一分支上，许多研究工作则致力于加速深网络层数，2014年， ILSVRC 比赛的亚军 VGGNet 全程使用 3*3的卷积，成功训练了深达19层的网络，当年的季军 MSRA-Net 也使用了非常深的网络。2015年，微软的ResNet成功训练了152层深的网络，一举拿下了当年 ILSVRC 比赛的冠军，top-5错误率降低至 3.46%。其后又更新了 ResNet V2 ，增加了 Batch Normalization，并去除了激活层而使用 Identity Mapping或 Preactivation，进一步提升了网络性能。此后，Inception ResNet V2融合了 Inception Net 优良的网络结构，和ResNet 训练极深网络的残差学习模块，集两个方向之长，取得了更好的分类结果。

　　我们可以看到，自AlexNet于2012 年提出后，深度学习领域的研究发展及其迅速，基本上每年甚至没几个月都会出现新一代的技术。新的技术往往伴随着新的网络结构，更深的网络的训练方法等，并在图像识别等领域不断创造新的准确率记录。至今，ILSVRC 比赛和卷积神经网络的研究依然处于高速发展期，CNN的技术日新月异。当然其中不可忽视的推动力是，我们拥有了更快的GPU计算资源用以实验，以及非常方便的开眼工具（比如TensorFlow）可以让研究人员快速的进行探索和尝试。在以前，研究人员如果没有像Alex那样高超的编程能力让自己实现 cuda-convert，可能都没办法设计 CNN或者快速地进行实验。现在有了 TensorFlow，研究人员和开发人员都可以简单而快速的设计神经网络结构并进行研究，测试，部署乃至使用。

八，CNN在MNIST数据集上的图像分类

　　代码如下：

# _*_coding:utf-8_*_
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
sess = tf.InteractiveSession()


# 权重和偏置需要创建，我们这里定义好初始化函数以便重复使用
# 这里我们使用截断的正态分布噪声，标准差设为0.1
def weight_varibale(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# 卷积层，池化层也是重复使用的，因此分别定义函数，以便后面重复使用
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1],
                          padding='SAME')


# 定义输入的： x 特征，y_ 真实的label
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
# 因为需要将1D 的输入向量转为2D的图片结构，而且颜色只有一个通道
# 所以最终尺寸如下，当然-1代表样本数量不固定，不用担心
x_image = tf.reshape(x, [-1, 28, 28, 1])

# 第一个卷积层
W_conv1 = weight_varibale([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 第二个卷积层（区别第一个卷积，卷积核变为64，也就是说这一层会提取64个特征）
W_conv2 = weight_varibale([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

# 当经历了两次步长为2*2的最大池化，所以边长已经只有1/4
# 所以图片尺寸由28*28边长7*7
W_fc1 = weight_varibale([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# 为了防止过拟合，下面使用一个Dropout层
# Dropout层是通过一个placeholder传入 keep_prob比率来控制的
# 在训练时候，我们随机丢掉一部分节点的数据来减轻过拟合
# 在预测时候，我们则保留全部数据来追求最好的预测性能
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 将Dropout层的输出连接一个Softmax层，得到最后的概率输出
W_fc2 = weight_varibale([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 定义损失函数cross_entropy，但是优化器使用Adam 并给予学习率1e-4
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y_conv),
                                              reduction_indices=[1]))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

tf.global_variables_initializer().run()
for i in range(20000):
    batch = mnist.train.next_batch(50)
    if i % 100 == 0:
        train_accuracy = accuracy.eval(feed_dict={
            x: batch[0], y_: batch[1], keep_prob: 1.0
        })
        print("step %d, training accuracy %g" % (i, train_accuracy))
    train_step.run(feed_dict={x: batch[0], y_: batch[1],
                              keep_prob: 0.5})

print("test accuracy %g" % accuracy.eval(feed_dict={
    x: mnist.test.images,
    y_: mnist.test.labels,
    keep_prob: 1.0
}))

　　结果如下：

step 0, training accuracy 0.1
step 100, training accuracy 0.9
step 200, training accuracy 0.86
step 300, training accuracy 0.92
step 400, training accuracy 0.92
step 500, training accuracy 0.94
step 600, training accuracy 0.98
step 700, training accuracy 0.96
......
step 7500, training accuracy 1
step 7600, training accuracy 0.98
... ...
step 19700, training accuracy 1
step 19800, training accuracy 1
step 19900, training accuracy 1
test accuracy 0.9929

　　最后，这个CNN模型可以得到的准确率约为99.29%，基本可以满足对手写数字识别准确率的要求。相比之前MLP的2%的错误率，CNN的错误率下降了大约60%，这其中主要的性能提升都来自于更优秀的网络设计，即卷积网络对图像特征的提取和抽象能力。依靠卷积核的权值共享，CNN的参数量并没有爆炸，降低计算量的同时也减轻了过拟合，因此整个模型的性能有较大的提升。

　　本文以CIFAR-10 为数据集，基于Tensorflow介绍CNN（卷积神经网络）图像分类模型的构建过程，着重分析了在建模过程中卷积层，池化层，扁平化层，全连接层，输出层的运算机理，以及经过运算后图像尺寸，数据维度等参数的变化情况。

九，CIFAR-10数据集介绍

　　官网地址：http://www.cs.toronto.edu/~kriz/cifar.html

　　Cifar数据集是一个影响力很大的图像分类数据集，Cifar数据集分为了Cifar-10和Cifar-100两个问题，他们都是图像词典项目（Visual Dictionary）中800万张图片的一个子集。

　　CIFAR-10数据集由60000张彩色图片构成，其中包括50000张训练集图片、10000张测试集图片，每张图片的shape为(32,32,3)，即图片尺寸为32*32，通道数为3；所有图片可以被分为10类，包括：

飞机， 汽车， 鸟， 猫， 鹿， 狗， 青蛙， 马， 船以及卡车。

　　官网截图如下所示：

　　和MNIST数据集类似，Cifar-10 中的图片大小都是固定的且每一张图片中仅仅包含一个种类的实体。但是和MNIST相比，Cifar数据集最大的区别在于图片由黑白变成的彩色，且分类的难度也相对更高。在Cifar-10数据集上，人工标注的正确率大概为94%，这比MNIST数据集上的人工表现要低很多。目前在Cifar-10数据集上最好的图像识别算法正确率为95.59%，达到这个正确率的算法使用了卷积神经网络。

　　本次学习的目标是建立一个用于识别图像的相对较小的卷积神经网络，在这过程中，我们将会学到：

　　1 着重建立一个规范的网络组织结构，训练兵进行评估

　　2 为建立更大规模更加复杂的模型提供一个范例

　　选择CIFAR-10是因为它的复杂程度足以用来检验TensorFlow中的大部分功能，并可将其扩展为更大的模型。与此同时由于模型较小所以训练速度很快，比较适合用来测试新的想法，检验新的技术。

代码组织

　　官网教程的代码位于tensorflow/models/image/cifar10/.

文件	作用
cifar10_input.py	读取本地CIFAR-10的二进制文件格式的内容。
cifar10.py	建立CIFAR-10的模型。
cifar10_train.py	在CPU或GPU上训练CIFAR-10的模型。
cifar10_multi_gpu_train.py	在多GPU上训练CIFAR-10的模型。
cifar10_eval.py	评估CIFAR-10模型的预测性能。

　　TensorFlow擅长训练深度神经网络，被认定为是神经网络中最好用的库之一。通过使用TensorFlow我们可以快速入门神经网络, 大大降低了深度学习（也就是深度神经网络）的开发成本和开发难度。 
　　Tensorflow使用数据流图进行数值计算，图中的节点代表数学运算，图中的边代表在这些节点之间传递的多维数组（张量）。在使用其构建模型时，先搭建好流图结构——类似于铺好管道，然后再加载数据——向管道中注水，让数据在各节点计算、沿各管道流动；数据在流图中计算、传递时采用多维数组(张量)的形式，因此在Tensorflow中参与计算的均为数组数据类型。 
　　本文使用Tensorflow构建简单的CNN图像多分类模型，其由3个卷积(含激活函数)与池化层、1个扁平层、3个全连接层、1个输出层构成，示意图如下所示： 

 

　　训练自己的图片（CNN）：https://blog.csdn.net/Missayaaa/article/details/79119839

　　该数据集的页面：http://www.cs.toronto.edu/~kriz/cifar.html

　　CIFAR-10和CIFAR-100是带有标签的数据集，都出自于规模更大的一个数据集，他有八千万张小图片（http://groups.csail.mit.edu/vision/TinyImages/。这个是一个大项目，你可以点击那个big map提交自己的标签，可以帮助他们训练让计算机识别物体的模型）

数据的下载：

• （共有三个版本：python,matlab,binary version 适用于C语言）
• http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
• http://www.cs.toronto.edu/~kriz/cifar-10-matlab.tar.gz
• http://www.cs.toronto.edu/~kriz/cifar-10-binary.tar.gz

 

十，CNN在Cifar-10数据集上的图像分类

　　代码：

#_*_coding:utf-8_*_
# import cifar10
import cifar10_input
import tensorflow as tf
import numpy as np
import time


max_steps = 3000
batch_size = 128
data_dir = 'cifar10\CIFAR-10\cifar-10-batches-bin'


def variable_with_weight_loss(shape, stddev, w1):
    '''
    权重初始化函数
    :param shape: 卷积核参数，格式类似于[5, 5, 3, 32]，代表卷积核尺寸（前两个数字通道数和卷积核个数）
    :param stddev:  标准差
    :param w1:  L2正则化的权重参数
    :return: 返回带有L2正则的初始化的权重参数
    '''
    # 截断产生正态分布，即产生正态分布的值与均值的差值大于两倍的标准差，那就重新写
    var = tf.Variable(tf.truncated_normal(shape, stddev=stddev))
    if w1 is not None:
        # 给权重W加上L2 正则，并用W1 参数控制L2 Loss大小
        weight_loss = tf.multiply(tf.nn.l2_loss(var), w1, name='weight_loss')
        # 将weight_loss 存在一个名为 “losses” 的collection里，后面会用到
        tf.add_to_collection('losses', weight_loss)
    return var

# 我们对图像进行数据增强的操作需要耗费大量CPU时间，因此distorted_inputs使用了16个
# 独立的线程来加速任务，函数内部会产生线程池，在需要使用时会通过queue进行调度。
images_train, labels_train = cifar10_input.distorted_inputs(
    data_dir=data_dir, batch_size=batch_size
)

# 生成测试数据
images_test, labels_test = cifar10_input.inputs(eval_data=True,
                                                data_dir=data_dir,
                                                batch_size=batch_size)

# 数据中图片的尺寸为24*24，即裁剪后的大小，而颜色的通道数则为3，代表RGB
image_holder = tf.placeholder(tf.float32, [batch_size, 24, 24, 3])
label_holder = tf.placeholder(tf.int32, [batch_size])

# 第一个卷积层
weight1 = variable_with_weight_loss(shape=[5, 5, 3, 64], stddev=5e-2,
                                    w1=0.0)
kernel1 = tf.nn.conv2d(image_holder, weight1, [1, 1, 1, 1],
                       padding='SAME')
bias1 = tf.Variable(tf.constant(0.0, shape=[64]))
conv1 = tf.nn.relu(tf.nn.bias_add(kernel1, bias1))
pool1 = tf.nn.max_pool(conv1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
                       padding='SAME')
norm1 = tf.nn.lrn(pool1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)

# 第二个卷积层，上一层卷积核数量为64，所以本层卷积核尺寸的第三个维度也需调整64
# 这里bias值全部初始化为0.1，而不是0，最后调整了最大池化层和LRN层的顺序，先LRN层处理
weight2 = variable_with_weight_loss(shape=[5, 5, 64, 64], stddev=5e-2, w1=0.0)
kernel2 = tf.nn.conv2d(norm1, weight2, [1, 1, 1, 1], padding='SAME')
bias2 = tf.Variable(tf.constant(0.1, shape=[64]))
conv2 = tf.nn.relu(tf.nn.bias_add(kernel2, bias2))
norm2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
pool2 = tf.nn.max_pool(norm2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
                       padding='SAME')

# 全连接层
reshape = tf.reshape(pool2, [batch_size, -1])
dim = reshape.get_shape()[1].value
weight3 = variable_with_weight_loss(shape=[dim, 384], stddev=0.04, w1=0.004)
bias3 = tf.Variable(tf.constant(0.1, shape=[384]))
local3 = tf.nn.relu(tf.matmul(reshape, weight3) + bias3)

# 全连接层2，和之前很像，只不过其隐含节点数下降了一半，只有192个，其他超参数不变
weight4 = variable_with_weight_loss(shape=[384, 192], stddev=0.04, w1=0.004)
bias4 = tf.Variable(tf.constant(0.1, shape=[192]))
local4 = tf.nn.relu(tf.matmul(local3, weight4) + bias4)

# 最后一层，先建立weight，其正态分布标准差为上一个隐含层的节点数的倒数，并且不计入L2正则
weight5 = variable_with_weight_loss(shape=[192, 10], stddev=1/192.0, w1=0.0)
bias5 = tf.Variable(tf.constant(0.0, shape=[10]))
logits = tf.add(tf.matmul(local4, weight5), bias5)

　　上面代码就完成了整个网络inference的部分。梳理整个网络结构可以得到如下表，从上到下，依次是整个卷积神经网络从输入到输出的流程。可以观察到，其实设计CNN主要就是安排卷积层，池化层，全连接层的分布和顺序，以及其中超参数的设计，Trick的使用等。设计性能良好的CNN一定有规律可循的，但是要想针对某个问题设计最合适的网络结构，是需要大量实践摸索的。

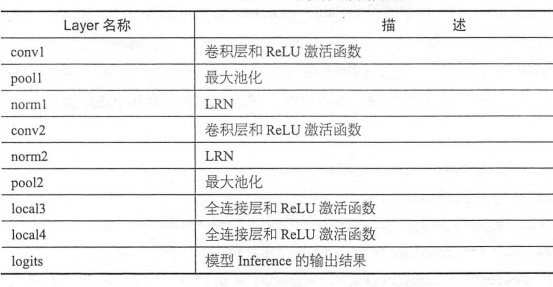
 　　完成了模型 inference 部分的构建，接下来计算 CNN的 loss。这里依然使用 cross_entropy，主要注意的是这里我们把softmax的计算和 cross_entropy_loss的计算合并在了一起。

#_*_coding:utf-8_*_
# import cifar10
import cifar10_input
import tensorflow as tf
import numpy as np
import time


max_steps = 3000   #训练轮数（每一轮一个batch参与训练）
batch_size = 128   # batch 大小
data_dir = 'cifar10\CIFAR-10\cifar-10-batches-bin' # 数据目录


def variable_with_weight_loss(shape, stddev, w1):
    '''
    权重初始化函数
    :param shape: 卷积核参数，格式类似于[5, 5, 3, 32]，代表卷积核尺寸（前两个数字通道数和卷积核个数）
    :param stddev:  标准差
    :param w1:  L2正则化的权重参数
    :return: 返回带有L2正则的初始化的权重参数
    '''
    # 截断产生正态分布，即产生正态分布的值与均值的差值大于两倍的标准差，那就重新写
    var = tf.Variable(tf.truncated_normal(shape, stddev=stddev))
    if w1 is not None:
        # 给权重W加上L2 正则，并用W1 参数控制L2 Loss大小
        weight_loss = tf.multiply(tf.nn.l2_loss(var), w1, name='weight_loss')
        # 将weight_loss 存在一个名为 “losses” 的collection里，后面会用到
        tf.add_to_collection('losses', weight_loss)
    return var

def loss(logits, labels):
    # 类型转换为 tf.int64
    labels = tf.cast(labels, tf.int64)
    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
        logits=logits, labels=labels,
        name='cross_entropy_per_example'
    )
    # 计算一个batch中交叉熵的均值
    cross_entropy_mean = tf.reduce_mean(cross_entropy,
                                        name='cross_entropy')
    # 将交叉熵存在 losses的collection
    tf.add_to_collection('losses', cross_entropy_mean)
    return tf.add_n(tf.get_collection('losses'), name='total_loss')

# 我们对图像进行数据增强的操作需要耗费大量CPU时间，因此distorted_inputs使用了16个
# 独立的线程来加速任务，函数内部会产生线程池，在需要使用时会通过queue进行调度。
# images_train, labels_train = cifar10_input.distorted_inputs(
#     data_dir=data_dir, batch_size=batch_size
# )
images_train, labels_train = cifar10_input.distorted_inputs(
    batch_size=batch_size
)

# 生成测试数据，每次执行都会生成一个 batch_size 的数量的测试样本
# images_test, labels_test = cifar10_input.inputs(eval_data=True,
#                                                 data_dir=data_dir,
#                                                 batch_size=batch_size)

images_test, labels_test = cifar10_input.inputs(eval_data=True,
                                                batch_size=batch_size)
# 数据中图片的尺寸为24*24，即裁剪后的大小，而颜色的通道数则为3，代表RGB
image_holder = tf.placeholder(tf.float32, [batch_size, 24, 24, 3])
label_holder = tf.placeholder(tf.int32, [batch_size])

# 第一个卷积层
# 第一层权重初始化，产生64个三通道（RGB图片），尺寸为5*5的卷积核，不带L2正则（w1=0）
weight1 = variable_with_weight_loss(shape=[5, 5, 3, 64], stddev=5e-2,
                                    w1=0.0)
# 对输出原始图像进行卷积操作，步长为[1, 1, 1, 1]即将每一个像素点都计算到
kernel1 = tf.nn.conv2d(image_holder, weight1, [1, 1, 1, 1],
                       padding='SAME')
# 定义第一层的偏置参数，由于有64个卷积核，这里有偏置尺寸为64
bias1 = tf.Variable(tf.constant(0.0, shape=[64]))
# 卷积结果加偏置后采用relu激活
conv1 = tf.nn.relu(tf.nn.bias_add(kernel1, bias1))
# 第一层的池化操作，使用尺寸为3*3，步长为2*2 的池化层进行操作
# 这里的ksize和strides 第一个和第四个数字一般都是1
pool1 = tf.nn.max_pool(conv1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
                       padding='SAME')
# 用LRN对结果进行处理，使用比较大的值变得更大，比较小的值变得更小，模仿神经系统的侧抑制机制
norm1 = tf.nn.lrn(pool1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)

# 第二个卷积层，上一层卷积核数量为64，所以本层卷积核尺寸的第三个维度也需调整64
# 这里bias值全部初始化为0.1，而不是0，最后调整了最大池化层和LRN层的顺序，先LRN层处理
weight2 = variable_with_weight_loss(shape=[5, 5, 64, 64], stddev=5e-2, w1=0.0)
kernel2 = tf.nn.conv2d(norm1, weight2, [1, 1, 1, 1], padding='SAME')
bias2 = tf.Variable(tf.constant(0.1, shape=[64]))
conv2 = tf.nn.relu(tf.nn.bias_add(kernel2, bias2))
norm2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
pool2 = tf.nn.max_pool(norm2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
                       padding='SAME')

# 全连接层
# 将上面的输出结果展平，-1代表不确定多大
reshape = tf.reshape(pool2, [batch_size, -1])
# 得到数据扁平化后的长度
dim = reshape.get_shape()[1].value
# 建立一个隐含节点数为384的全连接层
weight3 = variable_with_weight_loss(shape=[dim, 384], stddev=0.04, w1=0.004)
bias3 = tf.Variable(tf.constant(0.1, shape=[384]))
local3 = tf.nn.relu(tf.matmul(reshape, weight3) + bias3)

# 全连接层2，和之前很像，只不过其隐含节点数下降了一半，只有192个，其他超参数不变
weight4 = variable_with_weight_loss(shape=[384, 192], stddev=0.04, w1=0.004)
bias4 = tf.Variable(tf.constant(0.1, shape=[192]))
local4 = tf.nn.relu(tf.matmul(local3, weight4) + bias4)

# 最后一层，先建立weight，其正态分布标准差为上一个隐含层的节点数的倒数，并且不计入L2正则
weight5 = variable_with_weight_loss(shape=[192, 10], stddev=1/192.0, w1=0.0)
bias5 = tf.Variable(tf.constant(0.0, shape=[10]))
# 注意这里，直接是网络的原始输出（即wx+b 的形式），没有加softmax激活
logits = tf.add(tf.matmul(local4, weight5), bias5)


# 将logits节点和label_holder传入loss函数获得最终的loss
loss = loss(logits, label_holder)
#优化器依然选择 adam Optimizer 学习速率设置为1e-3
train_op = tf.train.AdamOptimizer(1e-3).minimize(loss)
# 关于tf.nn.in_top_k函数的用法见http://blog.csdn.net/uestc_c2_403/article/details/73187915
# tf.nn.in_top_k会返回一个[batch_size, classes(类别数)]大小的布尔型张量，记录是否判断正确
top_k_op = tf.nn.in_top_k(logits, label_holder, 1)

# 创建默认的session，接着初始化全部模型参数
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()

# 启动图片数据增强的线程队列，这里一共使用了16个线程来进行加速
# 注意：如果不启动线程，后续的inference及训练的操作都是无法开始的
tf.train.start_queue_runners()

for step in range(max_steps):
    start_time = time.time()
    # 获得一个batch的训练数据
    image_batch, label_batch = sess.run([images_train, labels_train])
    # 运行训练过程并获得一个batch的total_loss
    _, loss_value = sess.run([train_op, loss],
                             feed_dict={image_holder: image_batch,
                                        label_holder: label_batch})
    # 记录跑一个batch所耗费的时间
    duration = time.time() - start_time

    # 每10个batch输出信息
    if step % 10 == 0:
        # 计算每秒能跑多少个样本
        examples_per_sec = batch_size / duration
        # 计算每个batch需要耗费的时间
        sec_per_batch = float(duration)

        format_str = ('step %d, loss=%.2f(%.1f examples/sec; %.3f sec/batch)')
        print(format_str%(step, loss_value, examples_per_sec, sec_per_batch))


num_examples = 10000
import math
num_iter = int(math.ceil(num_examples / batch_size))
true_count = 0
total_sample_count = num_iter * batch_size
step = 0
while step < num_iter:
    image_batch, label_batch = sess.run([images_test, labels_test])
    predictions = sess.run([top_k_op], feed_dict={
        image_holder: image_batch, label_holder: label_batch
    })
    true_count += np.sum(predictions)
    step += 1

precision = true_count / total_sample_count
print('precsion @ 1 = %.3f' %precision)

　　部分结果如下：

step 0, loss=4.68(136.3 examples/sec; 0.939 sec/batch)
step 10, loss=3.66(187.9 examples/sec; 0.681 sec/batch)
step 20, loss=3.13(175.1 examples/sec; 0.731 sec/batch)
step 30, loss=2.83(181.5 examples/sec; 0.705 sec/batch)
step 40, loss=2.47(177.5 examples/sec; 0.721 sec/batch)
step 50, loss=2.25(185.2 examples/sec; 0.691 sec/batch)
step 60, loss=2.18(196.3 examples/sec; 0.652 sec/batch)
step 70, loss=2.12(191.3 examples/sec; 0.669 sec/batch)
step 80, loss=1.94(187.4 examples/sec; 0.683 sec/batch)
... ...
step 160, loss=1.86(206.4 examples/sec; 0.620 sec/batch)
step 170, loss=1.94(207.4 examples/sec; 0.617 sec/batch)
step 180, loss=1.85(209.8 examples/sec; 0.610 sec/batch)
... ...
step 310, loss=1.60(183.1 examples/sec; 0.699 sec/batch)
step 320, loss=1.57(193.3 examples/sec; 0.662 sec/batch)

　　

 

 补充1：特征图大小的计算

　　卷积中的特征图大小计算方式有两种，分别是“valid”和“same”，卷积和池化都使用。

　　如果计算方式采用“valid”：

　　如果计算方式采用“same”：

 

例题

　　输入图片大小为200×200，依次经过一层卷积（kernel size 5×5，padding 1，stride 2），pooling（kernel size 3×3，padding 0，stride 1），又一层卷积（kernel size 3×3，padding 1，stride 1）之后，输出特征图大小为：

A. 95

B. 96

C. 97

D. 98

E. 99

F. 100

解析：

（注意：除不尽的计算结果  卷积向下取整，池化向上取整）

卷积层和池化层输出大小计算公式

假设输入数据维度为W*W（一般长宽一样大，这样的话我们只需要计算一个维度即可），filter大小为F*F，步长（stride）为S，padding（需要填充的0的个数,指的是向外扩充的边缘大小）的像素为P，则：

　　　　　　输出尺寸 = （输入尺寸 - filter +2*padding）/stride +1

 

本题中 1层卷积：（200-5+2*1）/2+1 为99.5 ，取99，则输出99*99

　　　　池化层：（99-3）/1+1为97，输出为97*97

　　　 2层卷积：（97-3+2*1）/1+1 为97，输出97*97

研究过网络的话看到stride为1的时候，当kernel为 3 padding为1或者kernel为5 padding为2 一看就是卷积前后尺寸不变。

计算GoogLeNet全过程的尺寸也一样。

 

补充2：TensorFlow中CNN的两种padding方法‘SAME’和“VALID”

　　首先举个例子，代码如下：

import tensorflow as tf

x = tf.constant([[1.,2.,3.],[4.,5.,6.]])
print(x)  #Tensor("Const:0", shape=(2, 3), dtype=float32)
x = tf.reshape(x,[1,2,3,1])
print(x)   #Tensor("Reshape:0", shape=(1, 2, 3, 1), dtype=float32)

valid_pad = tf.nn.max_pool(x,[1,2,2,1],[1,2,2,1],padding='VALID')
same_pad = tf.nn.max_pool(x,[1,2,2,1],[1,2,2,1],padding='SAME')

print(valid_pad)  #Tensor("MaxPool:0", shape=(1, 1, 1, 1), dtype=float32)
print(same_pad)   #Tensor("MaxPool_1:0", shape=(1, 1, 2, 1), dtype=float32)

　　可以看出SAME的填充方式比VALID的填充方式多了一列。

　　让我们来看看变量x是一个2*3的矩阵，max_pooling窗口为2*2，两个维度的步长strides=2。

　　第一次由于窗口可以覆盖，橙色区域做max_pooling，没什么问题如下：

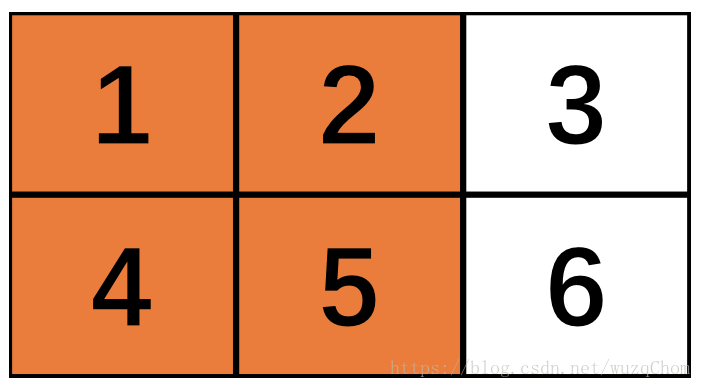
　　接下来，就是SAME和VALID的区别所在：由于步长为2，当向右滑动两步之后，VALID方式发现余下的窗口不到2*2，所以直接 将第三列舍去，而SAME方式不会把多出的一列丢弃，但是只有一列了，不够怎么办？所以会填充！（但是为了不影响原始信息，所以填0）

由上图所示，两个padding方式输出的形状不同，一个是截断，一个是填充

 

参考文献：https://blog.csdn.net/BaiHuaXiu123