Python机器学习笔记：异常点检测算法——One Class SVM
完整代码及其数据，请移步小编的GitHub
传送门：请点击我
如果点击有误：https://github.com/LeBron-Jian/MachineLearningNote
前言
最近老板有一个需求，做单样本检测，也就是说只有一个类别的数据集与标签，因为在工厂设备中，控制系统的任务是判断是是否有意外情况出现，例如产品质量过低，机器产生奇怪的震动或者机器零件脱落等。相对来说容易得到正常场景下的训练数据，但故障系统状态的收集示例数据可能相当昂贵，或者根本不可能。如果可以模拟一个错误的系统状态，问题就好解决多了，但无法保证所有的错误状态都被模拟到，所以只能寻找单样本检测相关的算法。
所幸了解到一些单样本检测的算法，比如Isolation Forest，One-Class Classification，所以这篇文章就记录一下自己做的关于One-Class SVM 的笔记。
一，单分类算法简介
One Class Learning 比较经典的算法是One-Class-SVM，这个算法的思路非常简单，就是寻找一个超平面将样本中的正例圈出来，预测就是用这个超平面做决策，在圈内的样本就认为是正样本。由于核函数计算比较耗时，在海量数据的场景用的并不多；
另一个算法是基于神经网络的算法，在深度学习中广泛使用的自编码算法可以应用在单分类的问题上，自编码是一个BP神经网络，网络输入层和输出层是一样，中间层数可以有多层，中间层的节点个数比输出层少，最简单的情况就是中间只有一个隐藏层，如下图所示，由于中间层的节点数较少，这样中间层相当于是对数据进行了压缩和抽象，实现无监督的方式学习数据的抽象特征。
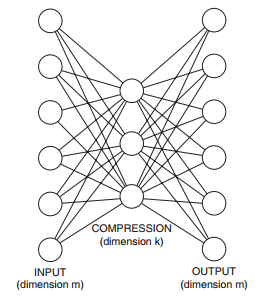
如果我们只有正样本数据，没有负样本数据，或者说只关注学习正样本的规律，那么利用正样本训练一个自编码器，编码器就相当于单分类的模型，对全量数据进行预测时，通过比较输入层和输出层的相似度就可以判断记录是否属于正样本。由于自编码采用神经网络实现，可以用GPU来进行加速计算，因此比较适合海量数据的场景。
还有Robust covariance 方法，基于协方差的稳健估计，假设数据是高斯分布的，那么在这样的案例中执行效果将优于One-Class SVM ；
最后就是Isolation Forest方法，孤立森林是一个高效的异常点检测算法。Sklearn提供了ensemble.IsolatuibForest模块。该模块在进行检测时，会随机选取一个特征，然后在所选特征的最大值和最小值随机选择一个分切面。该算法下整个训练集的训练就像一棵树一样，递归的划分。划分的次数等于根节点到叶子节点的路径距离d。所有随机树（为了增强鲁棒性，会随机选取很多树形成森林）的d的平均值，就是我们检测函数的最终结果。
孤立森林相关笔记可以参考这里：请点击我
Python机器学习笔记：异常点检测算法——Isolation Forest
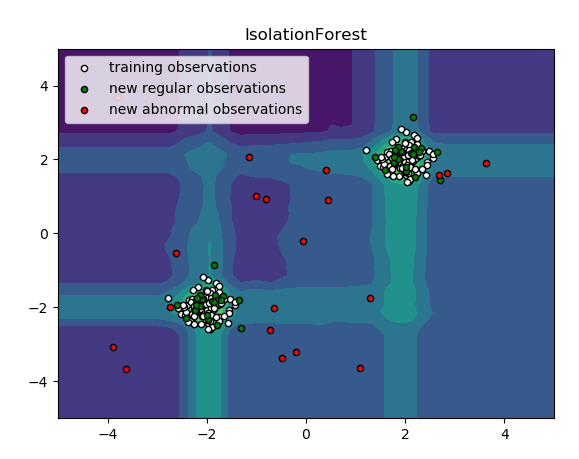
sklearn中关于异常检测的说法
Novelty and Outlier Detection
Many applications require being able to decide whether a new observation belongs to the same distribution as existing observations(it is an inlier), or should be considered as different (it is an outlier).Often, this ability is used to clean real data sets.Two import distinction must be made:
许多应用程序需要能够决定是否一个新的观察属于与存在观察点有相同分布（这是同类），或者应该被认为是不同的（它是个异类），通常这种能力是用来清洁真实数据集。两个差别如下：
novelty detection
The training data is not polluted by outliers, and we are interested in detecting anomalies in new observations.
当训练数据中没有离群点，我们的目标是用训练好的模型去检测另外发现的新样本
outlier dection
The training data contains outliers, and we need to fit the central mode of the training data, ignoring the deviant observations.
当训练数据中包含离群点，模型训练时要匹配训练数据的中心样本，忽视训练样本中的其他异常点。
sklearn提供了一些机器学习方法，可用于奇异（Novelty）点或者异常（Outlier）点检测，包括OneClassSVM，Isolation Forest，Local Outlier Factor（LOF）等，其中OneCLassSVM可以用于Novelty Dection，而后两者可用于Outlier Detection。
One-Class SVM 算法简介
严格来说，OneCLassSVM不是一种outlier detection，而是一种novelty detection方法：它的训练集不应该掺杂异常点，因为模型可能会去匹配这些异常点。但在数据维度很高，或者对相关数据分布没有任何假设的情况下，OneClassSVM也可以作为一种很好的outlier detection方法。
在one-class classification中，仅仅只有一类的信息是可以用于训练，其他类别的（总称outlier）信息是缺失的，也就是区分两个类别的边界线是通过仅有的一类数据的信息学习得到的。
OneClass 与二分类，多分类的区别
如果将分类算法进行划分，根据类别个数的不同可以分为单分类，二分类，多分类。常见的分类算法主要解决二分类和多分类问题，预测一封邮件是否是垃圾邮件是一个典型的二分类问题，手写体识别是一个典型的多分类问题，这些算法并不能很好的应用在单分类上，但是单分类问题在工业界广泛存在，由于每个企业刻画用户的数据都是有限的，很多二分类问题很难找到负样本，即使用一些排除法筛选出负样本，负样本也会不纯，不能保证负样本中没有正样本。所以在只能定义正样本不能定义负样本的场景中，使用单分类算法更合适。
单分类算法只关注与样本的相似或者匹配程度，对于未知的部分不妄下结论。
典型的二类问题：识别邮件是否是垃圾邮件，一类“是”，一类“不是”。
典型的多类问题：人脸识别，每个人对应的脸就是一个类，然后把待识别的脸分到对应的类去。
而OneClassClassification，它只有一个类，属于该类就返回结果“是”，不属于就返回结果“不是”。
其区别就是在二分类问题中，训练集中就由两个类的样本组成，训练出的模型是一个二分类模型；而OneClassClassification中的训练样本只有一类，因此训练出的分类器将不属于该类的所有其他样本判别为“不是”即可，而不是由于属于另一类才返回“不是”的结果。
现实场景中的OneCLassClassification例子：现在有一堆某商品的历史销售数据，记录着买该产品的用户信息，此外还有一些没有购买过该产品的用户信息，想通过二分类来预测他们是否会买该产品，也就是两个类，一类是“买”，一类是“不买”。当我们要开始训练二分类器的时候问题来了，一般来说没买的用户数会远远大于已经买了的用户数，当将数据不均衡的正负样本投入训练时，训练出的分类器会有较大的bisa（偏向值）。因此，这时候就可以使用OneClassClassification 方法来解决，即训练集中只有已经买过该产品的用户数据，在识别一个新用户是否会买该产品时，识别结果就是“会”或者“不会”。
One Class SVM算法步骤
One Class SVM也是属于支持向量机大家族的，但是它和传统的基于监督学习的分类回归支持向量机不同，它是无监督学习的方法，也就是说，它不需要我们标记训练集的输出标签。
那么没有类别标签，我们如何寻找划分的超平面以及寻找支持向量机呢？One Class SVM这个问题的解决思路有很多。这里只讲解一种特别的思想SVDD，对于SVDD来说，我们期望所有不是异常的样本都是正类别，同时它采用一个超球体而不是一个超平面来做划分，该算法在特征空间中获得数据周围的球形边界，期望最小化这个超球体的体积，从而最小化异常点数据的影响。
假设产生的超球体参数为中心 o 和对应的超球体半径 r >0，超球体体积V(r) 被最小化，中心 o 是支持行了的线性组合；跟传统SVM方法相似，可以要求所有训练数据点xi到中心的距离严格小于r。但是同时构造一个惩罚系数为 C 的松弛变量 ζi ,优化问题入下所示：
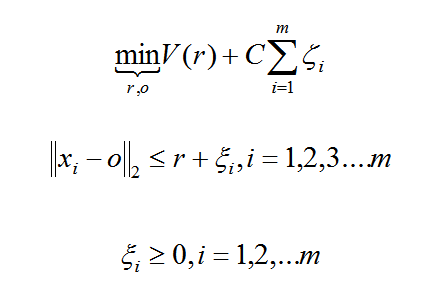
采用拉格朗日对偶求解之后，可以判断新的数据点 z 是否在内，如果 z 到中心的距离小于或者等于半径 r ，则不是异常点，如果在超球体以外，则是异常点。
在Sklearn中，我们可以采用SVM包里面的OneClassSVM来做异常点检测。OneClassSVM也支持核函数，所以普通SVM里面的调参思路在这里也使用。
SVDD算法介绍
SVDD（support vector domain description），中文翻译为：支持向量域描述。
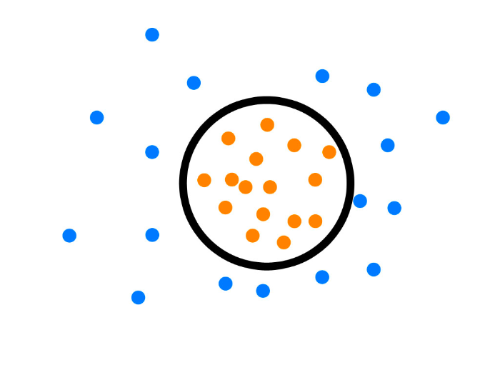
其基本思想是：既然只有一个class，那我就训练出一个最小的超球面（超球面是指三维以上的空间中的球面，对应的二维空间中就是曲线，三维空间中就是球面），将这堆数据全部“包起来”，识别一个新的数据点时，如果这个数据点落在超球面内，就属于这个类，否则不是。
例如对于二维（维数依据特征提取而定，提取的特征多，维数就搞，为了方便展示，举二维的例子，实际用时不可能维数这么低）数据，大概像下面这个样子：
有人可能会说：图上的曲线并没有把点全都包住，为什么会这样呢？其实看原理就懂了，下面学习一下SVDD的原理。
SVDD（support vector domain description）的原理和SVM（support vector machine）很像，可以用来做one class SVM，如果之前你看过SVM原理，那么下面的过程就很熟悉。
凡是将模型，都会有一个优化目标，SVDD的优化目标就是，求一个中心为a，半径为R的最小球面：
使得这个球面满足：
满足这个条件就是说要把training set中的数据点都包在球面里。
这里的
是松弛变量，和经典的SVM中的松弛变量的作用相同，它的作用就是，使得模型不会被个别极端的数据点给“破坏”了，想象一下，如果大多数的数据点都在一个小区域内，只有少数几个异常数据在离他们很远的地方，如果要找一个超球面把他们包住，这个超球面会很大，因为要包住那几个很远的点，这样就使得模型对离群点很敏感，说的通俗一点就是，那几个异常的点，虽然没法判断它是否真的是噪声数据，它是因为大数点都在一起，就少数几个不在这里，宁愿把那几个少数的数据点看成是异常的，以免模型为了迎合那几个少数的数据点会做出过大的牺牲，这就是所谓的过拟合（overfitting）。所以容忍一些不满足的硬性约束的数据点，给它一些弹性，同时又要包住training set中每个数据点都要满足约束，这样在后面才能使用Lagrange乘子法求解，因为Lagrange乘子法中是要包含约束条件的，如果你的数据都不满足约束条件，那就没法用了。注意松弛变量是带有下标 i 的，也就是说它是和每个数据点是有关系的，每个数据点都有对应的松弛变量，可以理解为：
对于每个数据点来说，那个超球面可以是不一样的，根据松弛变量来控制，如果松弛变量的值一样，那超球面就一样的，哪个C就是调节松弛变量的影响大小，说的通俗一点就是，给那些需要松弛的数据点多少松弛空间，如果C很大的话，那么在cost function中，由松弛变量带来的cost就大，那么training的时候会把松弛变量调小，这样的结果就是不怎么容忍那些离群点，硬是要把他们包起来，反之如果C比较小，那会给离群点较大的弹性，使得它们可以不被包含进行。现在就可以明白上面图为什么并没把点全都包住了。
下面展示两张图，第一张是C较小时候的情形，第二张图是C较大时的情形：
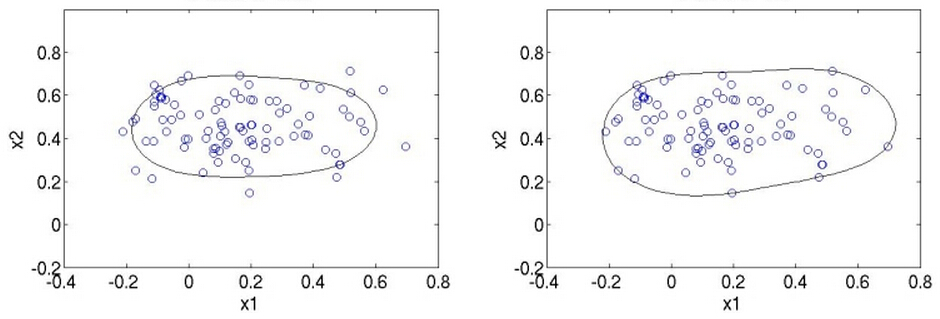
现在有了要求解的目标，又有了约束，接下来的求解方法和SVM几乎一样，用的是Lagrangian乘子法：
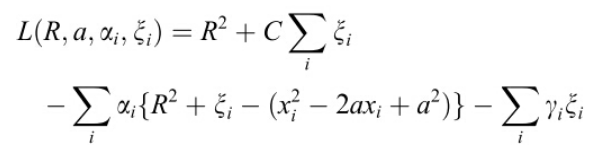
注意
和
，对参数求导并令导数等于0得到：
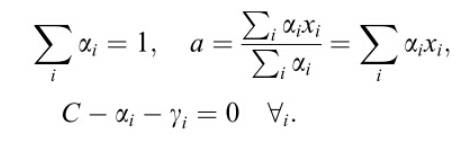
把上面公式带入Lagrangian函数，得到：
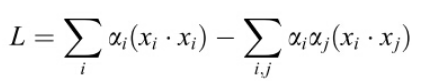
注意此时
，其中
是由
，
和
共同退出来的。上面的向量内积也可以像SVM那样用核函数解决：
之后的求解步骤就和SVM的一样了，具体请参考SVM原理。
训练结束后，判断一个新的数据点Z是否是这个类，那么就看这个数据点是否在训练出来的超球面里面，如果在里面，即
，则判定为属于这个类，将超球面的中心用支持向量来表示，那么判定新数据是否属于这个类的判定条件就是：
如果使用核函数那就是：
深度学习图片分类增强数据集的方法汇总
1，随机切割，图片反转，旋转等等很多方法都可以增加训练集，提高泛化能力
2，Resampling 或者增加噪音等等，人工合成更多的样本
3，对于小样本数据进行仿射变换，切割，旋转，加噪等各种处理，可以生成更多样本
4，用GAN生成数据提供给数据集
5，找个Imagenet数据集上训练好的模型，冻结最后一层或者最后几层，然后迁移学习 + fine tuning，图片数量少，做一些翻转，变化，剪切，白化等等。
6，水平翻转Flip，随机裁剪，平移变换Crops/Scales
所以最常用的方法就是：像素颜色抖动，旋转，剪切，随机裁剪，水平翻转，镜头拉伸和镜头矫正等等
sklearn实现：OneClasssSVM
根据已有支持向量机的理解，算法并非对已有标签的数据进行分类判别，而是通过回答：yes or no 的方法去根据支持向量域（support vector domaindescription SVDD），将样本数据训练出一个最小的超球面（大于三维特征），其中在二维中是一个曲线，将数据全部包起来，即将异常点排除。
OneClass SVM 主要参数和方法
class sklearn.svm.OneClassSVM(kernel=’rbf’, degree=3, gamma=’auto’, coef0=0.0, tol=0.001, nu=0.5, shrinking=True, cache_size=200, verbose=False, max_iter=-1, random_state=None)
参数：
kernel：核函数（一般使用高斯核）
nu：设定训练误差(0, 1]，表示异常点比例，默认值为0.5
属性：
方法：
fit(X)：训练，根据训练样本和上面两个参数探测边界。（注意是无监督）
predict(X)：返回预测值，+1就是正常样本，-1就是异常样本。
decision_function(X)：返回各样本点到超平面的函数距离（signed distance），正的维正常样本，负的为异常样本。
set_params(**params)：设置这个评估器的参数，该方法适用于简单估计器以及嵌套对象（例如管道），而后者具有表单<component>_<parameter>的参数，，因此可以更新嵌套对象的每个组件。
get_params([deep])：获取这个评估器的参数。
fit_predict(X[, y])：在X上执行拟合并返回X的标签，对于异常值，返回 -1 ，对于内点，返回1。
One-Class SVM with non-linear kernel （RBF）
下面使用OneClass SVM 进行奇异点检测。
OneClass SVM 是一个无监督算法，它用于学习奇异点检测的决策函数：将新数据分类为与训练集相似或者不同的数据。
数据结构
训练数据集 ：X_train——2*2
array([[ 2.21240237 2.05677141],
[ 2.2027219 1.58136665],
[ 1.99770721 1.93131038],
......
[ 1.73608122 2.0932801 ]]
)
这次训练，我们不用喂给分类器label，而是无监督的。
验证数据集 ：X_test——2*2
array([[ 2.13162953 2.58399607],
[ 2.15900993 1.96661511],
[ 2.20516139 2.01599965],
......
[ 2.14009567 1.98644128]])
离群点： X_outliers——2*2
array([[1.93385943 3.75727667],
[0.75210085 1.14235702],
......
[3.76820269 2.36662343])
预测的结果： y_pred_train：
[ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 -1 1 1 1 1 1 1 1
1 -1 1 1 -1 1 1 1 1 1 1 -1 -1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 -1 1 1 -1 1 1 1 -1 1 1 1 1 1 1 1 1 1 1 1 1
......
1 1 1 1 1 1 1 1]
预测的结果为 -1 或 1 ，在这个群落中为 1， 不在为 -1.
sklearn实现代码如下：
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# Generate train data
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
X_test = np.r_[X + 2, X-2]
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=0.1, high=4, size=(20, 2))
# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel='rbf', gamma=0.1)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outlier = y_pred_outliers[y_pred_outliers == 1].size
# plot the line , the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')
s =40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s, edgecolors='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s, edgecolors='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s, edgecolors='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
["learned frontier", 'training observations',
"new regular observations", "new abnormal observations"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel(
"error train: %d/200; errors novel regular: %d/40; errors novel abnormal:%d/40"%(
n_error_train, n_error_test, n_error_outlier) )
plt.show()
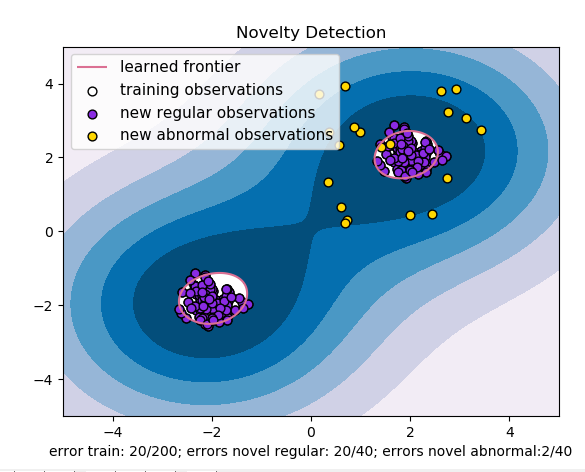
OneClassSVM 代码二
根据对已有支持向量机的理解，算法并非对已有标签的数据进行分类判别，而是通过回答“yes or no”的方式去根据支持向量域描述（support vector domaindescription SVDD），将样本数据训练出一个最小的超球面（大于三维特征），其中在二维中是一个曲线，将数据全部包起来，即将异常点排除。Sklearn包中给出的demo实验结果如上：我们可以看出在不同的数据分布下会有一些不一样的误差，其中调整参数中有一个比较重要的nu，表示异常点比例，默认值为0.5。
from sklearn import svm
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from numpy import genfromtxt
def read_dataset(filePath, delimiter=','):
return genfromtxt(filePath, delimiter=delimiter)
# use the same dataset
tr_data = read_dataset('tr_data.csv')
clf = svm.OneClassSVM(nu=0.05, kernel='rbf', gamma=0.1)
'''
OneClassSVM(cache_size=200, coef0=0.0, degree=3, gamma=0.1, kernel='rbf',
max_iter=-1, nu=0.05, random_state=None, shrinking=True, tol=0.001,
verbose=False)
'''
clf.fit(tr_data)
pred = clf.predict(tr_data)
# inliers are labeled 1 , outliers are labeled -1
normal = tr_data[pred == 1]
abnormal = tr_data[pred == -1]
plt.plot(normal[:, 0], normal[:, 1], 'bx)
plt.plot(abnormal[:, 0], abnormal[:, 1], 'ro')
因为上面的代码没有数据，我这里在网上找了一张图，可以基本说明问题，如下：
OneClassSVM 代码亲身实践
因为隐私原因，这里不贴出来数据，数据是475个正常的图和25个异常的图片，然后将图片进行转化，并进行灰度化处理，将其以矩阵的形式取出，因为OneClassSVM不需要标签，这里直接进行训练，然后预测原数据，得到了475个正常的结果和25个异常的结果，所以这里初步认为，OneClassSVM分类还是比较好的。
代码如下：
import numpy as np
import os
import cv2
from PIL import Image
import pandas as pd
import matplotlib.pyplot as plt
A = []
AA = []
def get_files(file_dir):
for file in os.listdir(file_dir + '/AA475_B25'):
A.append(file_dir + '/AA475_B25/' + file)
length_A = len(os.listdir(file_dir + '/AA475_B25'))
for file in range(length_A):
img = Image.open(A[file])
new_img = img.resize((128, 128))
new_img = new_img.convert("L")
matrix_img = np.asarray(new_img)
AA.append(matrix_img.flatten())
images1 = np.matrix(AA)
return images1
def OneClassSVM_train(data1):
from sklearn import svm
trainSet = data1
# nu 是异常点比例，默认是0.5
clf = svm.OneClassSVM(nu=0.05, kernel='linear', gamma=0.1)
clf.fit(trainSet)
y_pred_train = clf.predict(trainSet)
normal = trainSet[y_pred_train == 1]
abnormal = trainSet[y_pred_train == -1]
print(normal)
print(abnormal)
print(normal.shape)
print(abnormal.shape)
plt.plot(normal[:, 0], normal[:, 1], 'bx')
plt.plot(abnormal[:, 0], abnormal[:, 1], 'ro')
plt.show()
if __name__ == '__main__':
train_dir = '../one_variable/train'
data = get_files(train_dir)
OneClassSVM_train(data)
结果如下：
[[ 86 86 84 ... 50 51 48] [ 83 83 83 ... 143 59 59] [ 80 83 85 ... 45 47 45] ... [ 78 78 80 ... 56 59 54] [ 78 80 80 ... 191 191 178] [ 76 78 78 ... 56 54 54]] [[ 76 78 78 ... 62 62 64] [ 82 82 82 ... 82 82 82] [ 78 78 78 ... 51 51 51] ... [ 51 51 51 ... 31 31 31] [ 54 54 55 ... 29 29 29] [ 59 59 59 ... 185 185 185]] (475, 16384) (25, 16384)
最后，画出来展示的图如下：
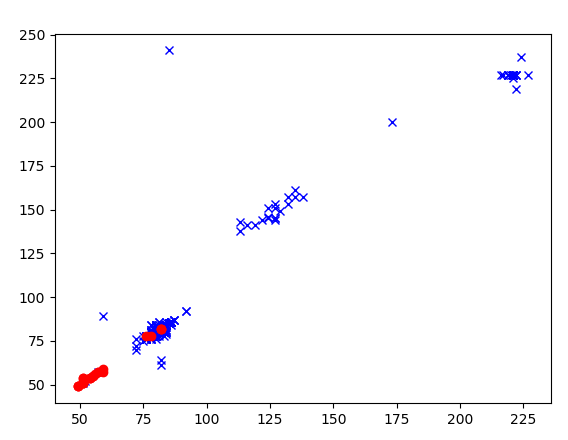
参考文献：
https://blog.csdn.net/bbbeoy/article/details/79159652
https://blog.csdn.net/u013719780/article/details/53219997
https://www.cnblogs.com/damumu/p/7320334.html
（这篇笔记，取之网络，还之网络）
