Python机器学习笔记：朴素贝叶斯算法
完整代码及其数据，请移步小编的GitHub
传送门：请点击我
如果点击有误：https://github.com/LeBron-Jian/MachineLearningNote
朴素贝叶斯是经典的机器学习算法之一，也是为数不多的基于概率论的分类算法。对于大多数的分类算法，在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。比如决策树，KNN，逻辑回归，支持向量机等，他们都是判别方法，也就是直接学习出特征输出Y和特征X之间的关系，要么是决策函数，要么是条件分布。但是朴素贝叶斯却是生成方法，该算法原理简单，也易于实现。
1，基本概念
朴素贝叶斯：贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯分类时贝叶斯分类中最简单，也是最常见的一种分类方法。
贝叶斯公式：
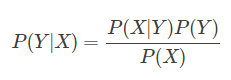
（X：特征向量， Y：类别）
先验概率P(X)：先验概率是指根据以往经验和分析得到的概率。
后验概率P(Y|X)：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小，后验分布P(Y|X)表示事件X已经发生的前提下，事件Y发生的概率，叫做事件X发生下事件Y的条件概率。
后验概率P(X|Y)：在已知Y发生后X的条件概率，也由于知道Y的取值而被称为X的后验概率。
朴素：朴素贝叶斯算法是假设各个特征之间相互独立，也是朴素这词的意思，那么贝叶斯公式中的P(X|Y)可写成：
朴素贝叶斯公式：
2，贝叶斯算法简介
贝叶斯方法源域它生前为解决一个“逆概”问题写的一篇文章。其要解决的问题：
正向概率：假设袋子里面有N个白球，M个黑球，你伸手进去摸一把，摸出黑球的概率是多大
逆向概率：如果我们事先不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或者好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例做出什么样的推测。
那么什么是贝叶斯呢？
- 1，现实世界本身就是不确定的，人类的观察能力是有局限性的
- 2，我们日常观察到的只是事物表明上的结果，因此我们需要提供一个猜测
NaiveBayes算法，又称朴素贝叶斯算法。朴素：特征条件独立；贝叶斯：基于贝叶斯定理。属于监督学习的生成模型，实现监督，没有迭代，并有坚实的数学理论（即贝叶斯定理）作为支撑。在大量样本下会有较好的表现，不适用于输入向量的特征条件有关联的场景。
朴素贝叶斯会单独考量每一维独立特征被分类的条件概率，进而综合这些概率并对其所在的特征向量做出分类预测。因此，朴素贝叶斯的基本数据假设是：各个维度上的特征被分类的条件概率之间是相互独立的。它经常被用于文本分类中，包括互联网新闻的分类，垃圾邮件的筛选。
朴素贝叶斯分类时一种十分简单的分类算法，叫他朴素贝叶斯分类时因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，即认为此待分类项属于哪个类别。
3，朴素贝叶斯的推导过程
贝叶斯学派很古老，但是从诞生到一百年前一直不是主流。主流是频率学派。频率学派的权威皮尔逊和费歇尔都对贝叶斯学派不屑一顾，但是贝叶斯学派硬是凭借着在现代特定领域的出色应用表现为自己赢得了半壁江山。
贝叶斯学派的思想可以概括为先验概率 + 数据 = 后验概率。也就是说我们在实际问题中需要得到的后验概率，可以通过先验概率和数据一起综合得到。数据大家好理解，被频率学派攻击的是先验概率，一般来说先验概率就是我们对于数据所在领域的历史经验，但是这个经验常常难以量化或者模型化，于是贝叶斯学派大胆的假设先验分布的模型，比如正态分布，beta分布等。这个假设一般没有特定的依据，因此一直被频率学派认为很荒谬。虽然难以从严密的数学逻辑推出贝叶斯学派的逻辑，但是在很多实际应用中，贝叶斯理论很好用，比如垃圾邮件分类，文本分类。
条件概率就是事件X在另外一个事件Y已经发生条件下的概率。条件概率表示为P(X|Y)。
我们先看看条件独立公式，如果X和Y相互独立，则由：
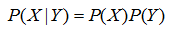
我们接着看条件概率公式：
或者说：
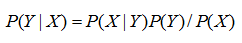
接着看看全概公式：
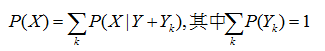
从上面的公式很容易得出贝叶斯公式：
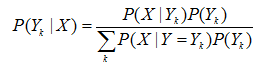
3.1 完整的推导过程
这里我们从条件概率的定义推导出贝叶斯定理，其实上面已经推导了，但是这个更简洁一些，所以使用一个叫联合概率的概念。
联合概率：表示两件事共同发生（数学概念上的交集）的概念，A和B的联合概率表示为
P(AnB)。
根据条件概率的定义，在事件B发生的条件下事件A发生的概率为：
同样地，在事件A发生的条件下事件B发生的概率为：
结合这两个方程式，我们可以得到：
这个引理有时称为概率乘法规则。上式两边同时除以P(A)，若P(A)是非零的，我们可以得到贝叶斯定理：
解释：事件X在事件Y发生的条件下的概率，与事件Y在事件X发生的条件下的概率是不一样的；然而这两者是有确定关系的，贝叶斯定理就是这种关系的陈述。
贝叶斯公式的用途在于通过已知三个概率来推测第四个概率。它的内容是：在 X 出现的前提下， Y 出现的概率等于 Y 出现的前提下 X 出现的概率乘以 Y 出现的概率再除以 X 出现的概率。通过联系X和Y，计算从一个事件发生的情况下另一事件发生的概率，即从结果上追溯到源头。
通俗地讲就是当你不能确定某一个事件发生的概率时，你可以依靠与该事件本质属性相关的时间发生的概率去推测该事件发生的概率。用数学语言表达就是：支持某项属性的事件发生的愈多，则该事件发生的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。
4，朴素贝叶斯的模型
从统计学知识回到我们的数据分析。假设我们的分类模型样本是：
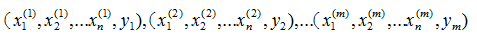
即我们有 m 个样本，每个样本有 n 个特征，特征输出有 K 个类别，定义为
。
从样本我们可以学习到朴素贝叶斯的先验分布
，接着学习到条件概率分布
，然后我们就可以用贝叶斯公式得到X 和 Y 的联合分布 P（X，Y）了。联合分布P（X，Y）定义为：
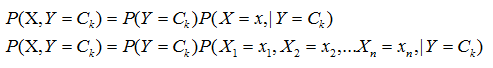
从上面的式子就可以看出
比较容易通过最大似然法求出，得到的
就是类别
在训练集里面出现的频数。但是
很难求出，这是一个超级复杂的有n个维度的条件分布。朴素贝叶斯模型在这里做一个大胆的假设，即 X 的n个维度之间相互独立，这样就可以得出：
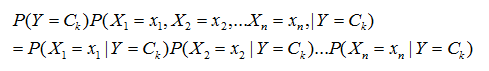
从上式可以看出，这个很难的条件分布大大的简化了，但是这也可能带来预测的不准确性。你会说我的特征之间非常不独立怎么办？如果真是非常不独立的话，那就尽量不要使用朴素贝叶斯模型了，考虑使用其他的分类方法比较好。但是一般情况下，样本的特征之间独立这个条件的确是弱成立的，尤其是数据量非常大的时候。虽然我们牺牲了准确性，但是得到的好处是模型的条件分布的计算大大简化了，这就是贝叶斯模型的选择。
最后回到我们要解决的问题，我们的问题是给定测试集的一个新样本特征
，我们如何判断它属于哪个类型？
既然是贝叶斯模型，当然是后验概率最大化来判断分类了。我们只要计算出所有的K个条件概率
，然后找出最大的条件概率对应的类别，这就是朴素贝叶斯的预测了。
5，一个简单的贝叶斯例子
举个简单的例子：
一个学校的男女比例为6:4，男生总是穿长裤，女生则一半穿长裤一半穿裙子。
正向概率：随机选出一个学生，他（她）穿长裤的概率和穿裙子的概率是多大
逆向概率：迎面走来一个穿长裤的学生，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别，你能够推断出他（她）是女生的概率是多大吗？
我们假设学校里面的总人数为 U 个
穿长裤的男生的概率为： U*P(Boy)*P(Pants|Boy)
P(Boy) 是男生的概率为：60%
P(Pants|Boy) 是条件概率，即在Boy这个条件下穿长裤的概率是多大，这里是 100%，因为男孩都穿长裤
穿长裤的女生的概率为：U*P(Girl)*P(Pants|Girl)
而我们要求解的是：穿长裤的人里面有多少是女生？
穿长裤的总人数为： U*P(Boy)*P(Pants|Boy) + U*P(Girl)*P(Pants|Girl)
P(Girl|Pants) = U * P(Girl) * P(Pants|Girl) / 穿长裤总数
即 P(Girl|Pants)= U * P(Girl) * P(Pants|Girl) / [ U*P(Boy)*P(Pants|Boy) + U*P(Girl)*P(Pants|Girl) ]
我们发现分母分子都有 U，那么我们可以消去：
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [ P(Boy)*P(Pants|Boy) + P(Girl)*P(Pants|Girl) ]
所以我们可以发现：
分母其实就是 P(Pants)
分子其实就是P(Pants, Girl)
所以：
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / P(Pants)
6，三种常见的贝叶斯模型
6.1，多项式模型（MultinomialNB）
多项式朴素贝叶斯常用语文本分类，特征是单词，值时单词出现的次数。
多项式模型在计算先验概率P(Yk)和和条件概率P(Xi|Yk)时，会做出一些平滑处理，具体公式为：
- N：样本数
- NYk：类别为Yk的样本数
- K：总的类别个数
- α：平滑值
- NYk,Xi：类别为Yk，且特征为X1的样本数
- n：特征X1可以选择的数量
6.2，高斯模型（GaussianNB）
当特征是连续变量的时候，假设特征分布为正态分布，根据样本算出均值和方差，再求得概率。
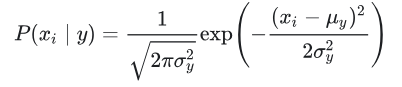
其中Ck为的第K类类别。Y的需要求出μk 和σk2 ，μk 在样本类别Ck中，所有 Xj 的平均值。σk2 为在样本类别 Ck 中，所有 Xj 的方差。
GaussianNB类的主要参数仅有一个，即先验概率priors，对应Y的各个类别的先验概率 P(Y=Ck)。这个值默认不给出，如果不给出此时P(Y=Ck) = mk/m。其中m为训练集样本总数量，mk为输出为第k类别的训练集样本数。如果给出的话就以priors为准。
在使用GaussianNB 的 fit方法拟合数据后，我们可以进行预测。此时预测有三种方法，包括predict，predict_log_proba 和 predict_proba。
predict方法就是我们最常用的预测方法，直接给出测试集的预测类别输出。
predict_proba则不同，它会给出测试集样本在各个类别上预测的概率。容易理解，predict_proba预测出的各个类别概率里最大值对应的类别，也就是predict方法得到类别。
predict_log_proba 和 predict_proba类似，它会给出测试集样本在各个类别上预测的概率的一个对数转化。转化后 predict_log_proba 预测出的各个类别对数概率里的最大值对应的类别，也就是 predict 方法得到类别。
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> from sklearn.naive_bayes import GaussianNB
>>> gnb = GaussianNB()
>>> y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
>>> print("Number of mislabeled points out of a total %d points : %d"
... % (iris.data.shape[0],(iris.target != y_pred).sum()))
Number of mislabeled points out of a total 150 points : 6
6.3，伯努利模型（BernoulliNB）
伯努利模型适用于离散特征的情况，伯努利模型中每个特征的取值只能是1和0。
此时 l 只有两种取值。Xjl只能取值0或者1。
BernoulliNB一共有四个参数，其中三个参数的名字和意义和MultinomialNB完全相同。唯一增加的一个参数是binarize。这个参数主要是用来帮BernoulliNB处理二项分布的，可以是数值或者不输入。如果不输入，则BernoulliNB认为每个数据特征已经是二元的。否则的话，小于binarize的会归为一类，大于 binarize的会归为另外一类。
在使用BernoulliNB 的fit 或者 partial_fit 方法拟合数据后，我们可以进行预测，此时预测方法有三种。包括predict，predict_log_proba和predict_proba。由于方法和GaussianNB完全一样，这里就不累述了。
7，算法流程
我们假设训练集为m个样本n个维度，如下：
共有K个特征输出类别，分别为C1，C2，...Ck，每个特征输出类别的样本个数为m1，m2，...mk，在第k 个类别中，如果是离散特征，则特征Xj各个类别取值为mjl。其中l取值为1,2，...Sj，Sj为特征j不同的取值数。
输出为实例X（test）的分类。
7.1，准备工作阶段
此阶段是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性，特征属性划分及训练样本质量决定。
1，如果没有Y的先验概率，则计算Y的K个先验概率：
，否则
为输入的先验概率。
2，分别计算第K个类别的第 j 维特征的第 l 个取值条件概率：
a) 如果是离散值：
λ 可以取值为1，或者其他大于0 的数字。
b）如果是稀疏二项离散值：
此时 l 只有两种取值。
c）如果是连续值不需要计算各个 l 的取值概率，直接求正态分布的参数：
需要求出μk 和σk2 ，μk 在样本类别Ck中，所有 Xj 的平均值。σk2 为在样本类别 Ck 中，所有 Xj 的方差。
3，对于实例 X(test)，分别计算：
4，确定实例 X(test) 的分类Cresult
从上面的计算可以看出，没有复杂的求导和矩阵运算，因此效率很高。
7.2，分类器训练阶段
这个阶段的认为就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入时特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。
7.3，应用阶段
这一阶段的任务是使用分类器对待分类项进行分类，其输入时分类器和待分类项，输出是待分类项和类别的映射关系。这一阶段也是机械性阶段，由程序完成。
8，朴素贝叶斯算法优缺点小结
8.1 优点
1，朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
2，对小规模的数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练
3，对缺失数据不太敏感，算法也比较简单，常用于文本分类。
8.2 缺点
1，理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小的时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2，需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3，由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
4，对输入数据的表达形式很敏感。
Sklearn朴素贝叶斯类库使用小结
官网地址：请点击我
朴素贝叶斯是一类比较简单的算法，scikit-learn中朴素贝叶斯类库的使用也比较简单。相对于决策树，KNN之类的算法，朴素贝叶斯需要关注的参数是比较少的，这样也比较容易掌握。
在scikit-learn中，提供了三种朴素贝叶斯分类算法：GaussianNB（高斯分布的朴素贝叶斯），MultinomailNB（先验为多项式分布的朴素贝叶斯），BernoulliNB（先验为伯努利分布的朴素贝叶斯）。
这三个类适用的分类场景各不相同，一般来说，如果样本特征的分布大部分是连续值，适用GaussianNB会比较好。如果样本特征的分布大部分是多元离散值，使用MultinomialNB比较合适。而如果样本特征是二元离散值或者很稀疏的多元离散值，应该使用BernoulliNB。
1，高斯朴素贝叶斯
sklearn.naive_bayes.GaussianNB(priors=None)
1.1 利用GaussianNB建立简单模型
import numpy as np from sklearn.naive_bayes import GaussianNB X = np.array([[-1, -1], [-2, -2], [-3, -3], [-4, -4], [1, 1], [2, 2], [3, 3]]) y = np.array([1, 1, 1, 1, 2, 2, 2]) clf = GaussianNB() re = clf.fit(X, y) print(re) # GaussianNB(priors=None, var_smoothing=1e-09)
1.2 经过训练集训练后，观察各个属性值
re1 = clf.priors # print(re1) #None # 设置priors参数值 re2 = clf.set_params(priors=[0.625, 0.375]) # print(re2) # GaussianNB(priors=[0.625, 0.375], var_smoothing=1e-09) # 返回各类标记对应先验概率组成的列表 re3 = clf.priors # print(re3) # [0.625, 0.375]
1.3 priors属性：获取各个类标记对应的先验概率
re4 = clf.class_prior_ # print(re4) # [0.57142857 0.42857143] re5 = type(clf.class_prior_) # print(re5) # <class 'numpy.ndarray'>
1.4 class_prior_属性：同priors一样，都是获取各个类标记对应的先验概率，区别在于priors属性返回列表，class_prior_返回的是数组
re6 = clf.class_count_ # print(re6) # [4. 3.]
1.5 class_count_属性：获取各类标记对应的训练样本数
re6 = clf.class_count_ # print(re6) # [4. 3.]
1.6 theta_属性：获取各个类标记在各个特征上的均值
re7 = clf.theta_ # print(re7) # [[-2.5 -2.5] # [ 2. 2. ]]
1.7 sigma_属性：获取各个类标记在各个特征上的方差
re8 = clf.sigma_ # print(re8) # [[1.25000001 1.25000001] # [0.66666667 0.66666667]]
1.8 方法
- get_params(deep=True)：返回priors与其参数值组成字典
re9 = clf.get_params(deep=True)
# print(re9)
# {'priors': [0.625, 0.375], 'var_smoothing': 1e-09}
re10 = clf.get_params()
# print(re10)
# {'priors': [0.625, 0.375], 'var_smoothing': 1e-09}
- set_params(**params)：设置估计器priors参数
re11 = clf.set_params(priors=[0.625, 0.375]) # print(re11) # GaussianNB(priors=[0.625, 0.375], var_smoothing=1e-09)
- fit(X, sample_weight=None)：训练样本，X表示特征向量，y类标记，sample_weight表示各样本权重数组
In [12]: clf.fit(X,y,np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))#设置样本不同的权重
Out[12]: GaussianNB(priors=[0.625, 0.375])
In [13]: clf.theta_
Out[13]:
array([[-3.375, -3.375],
[ 2. , 2. ]])
In [14]: clf.sigma_
Out[14]:
array([[ 1.73437501, 1.73437501],
[ 0.66666667, 0.66666667]])
- partial_fit(X, y, classes=None, sample_weight=None)：增量式训练，当训练数据集数据量非常大，不能一次性全部载入内存时，可以将数据集划分若干份，重复调用partial_fit在线学习模型参数，在第一次调用partial_fit函数时，必须指定classes参数，在随后的的调用可以忽略。
In [18]: import numpy as np
...: from sklearn.naive_bayes import GaussianNB
...: X = np.array([[-1, -1], [-2, -2], [-3, -3],[-4,-4],[-5,-5], [1, 1], [2
...: , 2], [3, 3]])
...: y = np.array([1, 1, 1,1,1, 2, 2, 2])
...: clf = GaussianNB()#默认priors=None
...: clf.partial_fit(X,y,classes=[1,2],sample_weight=np.array([0.05,0.05,0.
...: 1,0.1,0.1,0.2,0.2,0.2]))
...:
Out[18]: GaussianNB(priors=None)
In [19]: clf.class_prior_
Out[19]: array([ 0.4, 0.6])
- predict(X)：直接输出测试集预测的类标记
In [20]: clf.predict([[-6,-6],[4,5]]) Out[20]: array([1, 2])
- predict_proba(X)：输出测试样本在各个类标记预测概率值
In [21]: clf.predict_proba([[-6,-6],[4,5]])
Out[21]:
array([[ 1.00000000e+00, 4.21207358e-40],
[ 1.12585521e-12, 1.00000000e+00]])
- predict_log_proba(X)：输出测试样本在各个类标记上预测概率值对应对数值
In [22]: clf.predict_log_proba([[-6,-6],[4,5]])
Out[22]:
array([[ 0.00000000e+00, -9.06654487e+01],
[ -2.75124782e+01, -1.12621024e-12]])
- score(X, y, sample_weight=None)：返回测试样本映射到指定类标记上的得分(准确率)
In [23]: clf.score([[-6,-6],[-4,-2],[-3,-4],[4,5]],[1,1,2,2])
Out[23]: 0.75
In [24]: clf.score([[-6,-6],[-4,-2],[-3,-4],[4,5]],[1,1,2,2],sample_weight=[0.3
...: ,0.2,0.4,0.1])
Out[24]: 0.59999999999999998
2，多项式朴素贝叶斯
主要用于离散特征分类，例如文本分类单词统计，以出现的次数作为特征值
sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
参数说明：
alpha：浮点型，可选项，默认1.0，添加拉普拉修/Lidstone平滑参数 fit_prior：布尔型，可选项，默认True，表示是否学习先验概率，参数为 False表示所有类标记具有相同的先验概率 class_prior：类似数组，数组大小为(n_classes,)，默认None，类先验概率
2.1 利用MultinomialNB建立简单模型
In [2]: import numpy as np ...: from sklearn.naive_bayes import MultinomialNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6, ...: 6]]) ...: y = np.array([1,1,4,2,3,3]) ...: clf = MultinomialNB(alpha=2.0) ...: clf.fit(X,y) ...: Out[2]: MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
2.2 经过训练后，观察各个属性值
- class_log_prior_：各类标记的平滑先验概率对数值，其取值会受fit_prior和class_prior参数的影响
若指定了class_prior参数，不管fit_prior为True或False，class_log_prior_取值是class_prior转换成log后的结果
In [4]: import numpy as np ...: from sklearn.naive_bayes import MultinomialNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6, ...: 6]]) ...: y = np.array([1,1,4,2,3,3]) ...: clf = MultinomialNB(alpha=2.0,fit_prior=True,class_prior=[0.3,0.1,0.3,0 ...: .2]) ...: clf.fit(X,y) ...: print(clf.class_log_prior_) ...: print(np.log(0.3),np.log(0.1),np.log(0.3),np.log(0.2)) ...: clf1 = MultinomialNB(alpha=2.0,fit_prior=False,class_prior=[0.3,0.1,0.3 ...: ,0.2]) ...: clf1.fit(X,y) ...: print(clf1.class_log_prior_) ...: [-1.2039728 -2.30258509 -1.2039728 -1.60943791] -1.20397280433 -2.30258509299 -1.20397280433 -1.60943791243 [-1.2039728 -2.30258509 -1.2039728 -1.60943791]
若fit_prior参数为False，class_prior=None，则各类标记的先验概率相同等于类标记总个数N分之一
In [5]: import numpy as np ...: from sklearn.naive_bayes import MultinomialNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6, ...: 6]]) ...: y = np.array([1,1,4,2,3,3]) ...: clf = MultinomialNB(alpha=2.0,fit_prior=False) ...: clf.fit(X,y) ...: print(clf.class_log_prior_) ...: print(np.log(1/4)) ...: [-1.38629436 -1.38629436 -1.38629436 -1.38629436] -1.38629436112
若fit_prior参数为True，class_prior=None，则各类标记的先验概率相同等于各类标记个数处以各类标记个数之和
In [6]: import numpy as np ...: from sklearn.naive_bayes import MultinomialNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6, ...: 6]]) ...: y = np.array([1,1,4,2,3,3]) ...: clf = MultinomialNB(alpha=2.0,fit_prior=True) ...: clf.fit(X,y) ...: print(clf.class_log_prior_)#按类标记1、2、3、4的顺序输出 ...: print(np.log(2/6),np.log(1/6),np.log(2/6),np.log(1/6)) ...: [-1.09861229 -1.79175947 -1.09861229 -1.79175947] -1.09861228867 -1.79175946923 -1.09861228867 -1.79175946923
- intercept_：将多项式朴素贝叶斯解释的class_log_prior_映射为线性模型，其值和class_log_propr相同
In [7]: clf.class_log_prior_ Out[7]: array([-1.09861229, -1.79175947, -1.09861229, -1.79175947]) In [8]: clf.intercept_ Out[8]: array([-1.09861229, -1.79175947, -1.09861229, -1.79175947])
- feature_log_prob_：指定类的各特征概率（条件概率）对数值，返回形状为（n_classes, n_features）数组
In [9]: clf.feature_log_prob_
Out[9]:
array([[-2.01490302, -1.45528723, -1.2039728 , -1.09861229],
[-1.87180218, -1.31218639, -1.178655 , -1.31218639],
[-1.74919985, -1.43074612, -1.26369204, -1.18958407],
[-1.79175947, -1.38629436, -1.23214368, -1.23214368]])
特征条件概率计算过程，以类为1各个特征对应的条件概率为例
In [9]: clf.feature_log_prob_
Out[9]:
array([[-2.01490302, -1.45528723, -1.2039728 , -1.09861229],
[-1.87180218, -1.31218639, -1.178655 , -1.31218639],
[-1.74919985, -1.43074612, -1.26369204, -1.18958407],
[-1.79175947, -1.38629436, -1.23214368, -1.23214368]])
In [10]: print(np.log((1+1+2)/(1+2+3+4+1+3+4+4+4*2)),np.log((2+3+2)/(1+2+3+4+1+
...: 3+4+4+4*2)),np.log((3+4+2)/(1+2+3+4+1+3+4+4+4*2)),np.log((4+4+2)/(1+2+
...: 3+4+1+3+4+4+4*2)))
-2.01490302054 -1.45528723261 -1.20397280433 -1.09861228867
特征的条件概率=（指定类下指定特征出现的次数+alpha）/（指定类下所有特征出现次数之和+类的可能取值个数*alpha）
- coef_：将多项式朴素贝叶斯解释feature_log_prob_映射成线性模型，其值和feature_log_prob相同
In [11]: clf.coef_
Out[11]:
array([[-2.01490302, -1.45528723, -1.2039728 , -1.09861229],
[-1.87180218, -1.31218639, -1.178655 , -1.31218639],
[-1.74919985, -1.43074612, -1.26369204, -1.18958407],
[-1.79175947, -1.38629436, -1.23214368, -1.23214368]])
- class_count_：训练样本中各类别对应的样本数，按类的顺序排序输出
In [12]: clf.class_count_ Out[12]: array([ 2., 1., 2., 1.])
- feature_count_：各类别各个特征出现的次数，返回形状为(n_classes, n_features)数组
In [13]: clf.feature_count_
Out[13]:
array([[ 2., 5., 7., 8.],
[ 2., 5., 6., 5.],
[ 6., 9., 11., 12.],
[ 2., 4., 5., 5.]])
In [14]: print([(1+1),(2+3),(3+4),(4+4)])#以类别1为例
[2, 5, 7, 8]
2.3 方法
- fit(X, y, sample_weight=None)：根据X、y训练模型
In [15]: import numpy as np
...: from sklearn.naive_bayes import MultinomialNB
...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6
...: ,6]])
...: y = np.array([1,1,4,2,3,3])
...: clf = MultinomialNB(alpha=2.0,fit_prior=True)
...: clf.fit(X,y)
...:
Out[15]: MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
- get_params(deep=True)：获取分类器的参数，以各参数字典形式返回
In [16]: clf.get_params(True)
Out[16]: {'alpha': 2.0, 'class_prior': None, 'fit_prior': True}
- partial_fit(X, y, classes=None, sample_weight=None)：对于数据量大时，提供增量式训练，在线学习模型参数，参数X可以是类似数组或稀疏矩阵，在第一次调用函数，必须制定classes参数，随后调用时可以忽略
In [17]: import numpy as np
...: from sklearn.naive_bayes import MultinomialNB
...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6
...: ,6]])
...: y = np.array([1,1,4,2,3,3])
...: clf = MultinomialNB(alpha=2.0,fit_prior=True)
...: clf.partial_fit(X,y)
...: clf.partial_fit(X,y,classes=[1,2])
...:
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-17-b512d165c9a0> in <module>()
4 y = np.array([1,1,4,2,3,3])
5 clf = MultinomialNB(alpha=2.0,fit_prior=True)
----> 6 clf.partial_fit(X,y)
7 clf.partial_fit(X,y,classes=[1,2])
ValueError: classes must be passed on the first call to partial_fit.
In [18]: import numpy as np
...: from sklearn.naive_bayes import MultinomialNB
...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6
...: ,6]])
...: y = np.array([1,1,4,2,3,3])
...: clf = MultinomialNB(alpha=2.0,fit_prior=True)
...: clf.partial_fit(X,y,classes=[1,2])
...: clf.partial_fit(X,y)
...:
...:
Out[18]: MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
- predict(X)：在测试集X上预测，输出X对应目标值
In [19]: clf.predict([[1,3,5,6],[3,4,5,4]]) Out[19]: array([1, 1]）
- predict_log_proba(X)：测试样本划分到各个类的概率对数值
In [22]: import numpy as np
...: from sklearn.naive_bayes import MultinomialNB
...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6
...: ,6]])
...: y = np.array([1,1,4,2,3,3])
...: clf = MultinomialNB(alpha=2.0,fit_prior=True)
...: clf.fit(X,y)
...:
Out[22]: MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
In [23]: clf.predict_log_proba([[3,4,5,4],[1,3,5,6]])
Out[23]:
array([[-1.27396027, -1.69310891, -1.04116963, -1.69668527],
[-0.78041614, -2.05601551, -1.28551649, -1.98548389]])
- predict_proba(X)：输出测试样本划分到各个类别的概率值
In [1]: import numpy as np ...: from sklearn.naive_bayes import MultinomialNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6, ...: 6]]) ...: y = np.array([1,1,4,2,3,3]) ...: clf = MultinomialNB(alpha=2.0,fit_prior=True) ...: clf.fit(X,y) ...: Out[1]: MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True) In [2]: clf.predict_proba([[3,4,5,4],[1,3,5,6]]) Out[2]: array([[ 0.27972165, 0.18394676, 0.35304151, 0.18329008],
- score(X, y, sample_weight=None)：输出对测试样本的预测准确率的平均值
In [3]: clf.score([[3,4,5,4],[1,3,5,6]],[1,1]) Out[3]: 0.5
- set_params(**params)：设置估计器的参数
In [4]: clf.set_params(alpha=1.0) Out[4]: MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
3，伯努利朴素贝叶斯
类似于多项式朴素贝叶斯，也主要用于离散特征分类，和MultinomialNB的区别是：MultinomialNB以出现的次数为特征值，BernnoulliNB为二进制或者布尔值特征
sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True,class_prior=None)
参数说明：
binarize：将数据特征二值化的阈值
3.1 利用BernoulliNB建立简单模型
In [5]: import numpy as np ...: from sklearn.naive_bayes import BernoulliNB ...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5]]) ...: y = np.array([1,1,2]) ...: clf = BernoulliNB(alpha=2.0,binarize = 3.0,fit_prior=True) ...: clf.fit(X,y) ...: Out[5]: BernoulliNB(alpha=2.0, binarize=3.0, class_prior=None, fit_prior=True)
经过binarize=0.3二值化处理，相当于输入的X数组为：
In [7]: X = np.array([[0,0,0,1],[0,0,1,1],[0,1,1,1]])
In [8]: X
Out[8]:
array([[0, 0, 0, 1],
[0, 0, 1, 1],
[0, 1, 1, 1]])
3.2 训练后查看个属性值
- class_log_prior_：类先验概率对数值，类先验概率等于各类的个数/类的总个数
In [9]: clf.class_log_prior_ Out[9]: array([-0.40546511, -1.09861229])
- feature_log_prob_ :指定类的各特征概率(条件概率)对数值，返回形状为(n_classes, n_features)数组
Out[10]:
array([[-1.09861229, -1.09861229, -0.69314718, -0.40546511],
[-0.91629073, -0.51082562, -0.51082562, -0.51082562]])
In [11]: import numpy as np
...: from sklearn.naive_bayes import BernoulliNB
...: X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5]])
...: y = np.array([1,1,2])
...: clf = BernoulliNB(alpha=2.0,binarize = 3.0,fit_prior=True)
...: clf.fit(X,y)
...: print(clf.feature_log_prob_)
...: print([np.log((2+2)/(2+2*2))*0+np.log((0+2)/(2+2*2))*1,np.log((2+2)/(2
...: +2*2))*0+np.log((0+2)/(2+2*2))*1,np.log((1+2)/(2+2*2))*0+np.log((1+2)/
...: (2+2*2))*1,np.log((0+2)/(2+2*2))*0+np.log((2+2)/(2+2*2))*1])
...:
[[-1.09861229 -1.09861229 -0.69314718 -0.40546511]
[-0.91629073 -0.51082562 -0.51082562 -0.51082562]]
[-1.0986122886681098, -1.0986122886681098, -0.69314718055994529, -0.405465108108
16444]
- class_count_：按类别顺序输出其对应的个数
In [12]: clf.class_count_ Out[12]: array([ 2., 1.])
- feature_count_：各类别各特征值之和，按类的顺序输出，返回形状为[n_classes, n_features] 的数组
In [13]: clf.feature_count_
Out[13]:
array([[ 0., 0., 1., 2.],
[ 0., 1., 1., 1.]])
3.3 方法
类似于MultinomialNB的方法类似
Sklearn实战一（多项式朴素贝叶斯）
朴素贝叶斯模型被广泛应用于海量互联网文本分类任务。由于其较强的特征条件独立假设，使得模型预测所需要顾及的参数规模从幂指数数量级向线性量级减少，极大的节约了内存消耗和计算时间。但是，也正是受这种强假设的限制，模型训练时无法将各个特征之间的联系考量在内，使得该模型在其他数据特征关联性较强的分类任务上性能表现不佳。
代码：
#_*_coding:utf-8_*_
# 从sklearn.datasets中导入新闻数据抓取器
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
# 从sklearn.feature_extraction.text里导入文本特征向量化模板
from sklearn.feature_extraction.text import CountVectorizer
# 从sklearn.naive_bayes里导入朴素贝叶斯模型
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
# 数据获取
news = fetch_20newsgroups(subset='all')
# 输出数据的条数 18846
print(len(news.data))
# 数据预处理：训练集和测试集分割，文本特征向量化
# 随机采样25%的数据样本作为测试集
X_train, X_test, y_train, y_test = train_test_split(
news.data, news.target, test_size=0.25, random_state=33
)
# # 查看训练样本
# print(X_train[0])
# # 查看标签
# print(y_train[0:100])
# 文本特征向量化
vec = CountVectorizer()
X_train = vec.fit_transform(X_train)
X_test = vec.transform(X_test)
# 使用朴素贝叶斯进行训练
# 使用默认配置初始化朴素贝叶斯
mnb = MultinomialNB()
# 利用训练数据对模型参数进行估计
mnb.fit(X_train, y_train)
# 对参数进行预测
y_predict = mnb.predict(X_test)
# 获取结果报告
score = mnb.score(X_test, y_test)
print('The accuracy of Naive bayes Classifier is %s' %score)
res = classification_report(y_test, y_predict, target_names=news.target_names)
print(res)
结果如下：
The accuracy of Naive bayes Classifier is 0.8397707979626485
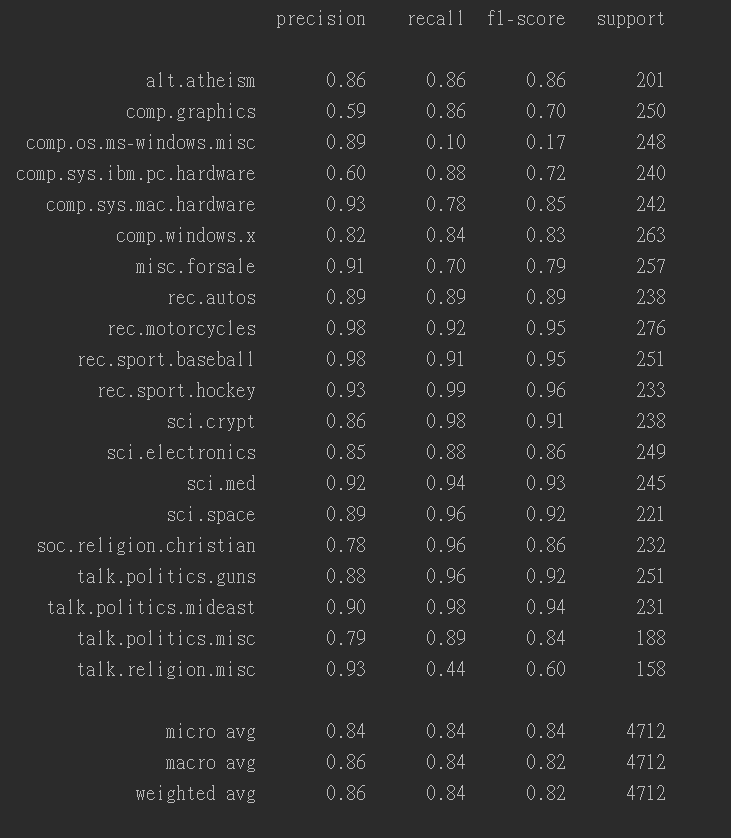
Sklearn实战二（多项式朴素贝叶斯）
代码：
#_*_coding:utf-8_*_
import pandas as pd
import numpy as np
import cv2
import time
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 获取数据
def load_data():
# 读取csv数据
raw_data = pd.read_csv('train.csv', header=0)
data = raw_data.values
features = data[::, 1::]
labels = data[::, 0]
# 避免过拟合，采用交叉验证，随机选取33%数据作为测试集，剩余为训练集
train_X, test_X, train_y, test_y = train_test_split(features, labels, test_size=0.33, random_state=0)
return train_X, test_X, train_y, test_y
# 二值化处理
def binaryzation(img):
# 类型转化成Numpy中的uint8型
cv_img = img.astype(np.uint8)
# 大于50的值赋值为0，不然赋值为1
cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img)
return cv_img
# 训练，计算出先验概率和条件概率
def Train(trainset, train_labels):
# 先验概率
prior_probability = np.zeros(class_num)
# 条件概率
conditional_probability = np.zeros((class_num, feature_len, 2))
# 计算
for i in range(len(train_labels)):
# 图片二值化，让每一个特征都只有0， 1 两种取值
img = binaryzation(trainset[i])
label = train_labels[i]
prior_probability[label] += 1
for j in range(feature_len):
conditional_probability[label][j][img[j]] += 1
# 将条件概率归到 [1, 10001]
for i in range(class_num):
for j in range(feature_len):
# 经过二值化后图像只有0， 1 两种取值
pix_0 = conditional_probability[i][i][0]
pix_1 = conditional_probability[i][j][1]
# 计算0， 1像素点对应的条件概率
probability_0 = (float(pix_0)/float(pix_0 + pix_1))*10000 + 1
probability_1 = (float(pix_1)/float(pix_0 + pix_1))*10000 + 1
conditional_probability[i][j][0] = probability_0
conditional_probability[i][j][1] = probability_1
return prior_probability, conditional_probability
# 计算概率
def calculate_probability(img, label):
probability = int(prior_probability[label])
for j in range(feature_len):
probability *= int(conditional_probability[label][j][img[j]])
return probability
# 预测
def Predict(testset, prior_probability, conditional_probability):
predict = []
# 对于每个输入的X，将后验概率最大的类作为X的类输出
for img in testset:
# 图像二值化
img = binaryzation(img)
max_label = 0
max_probability = calculate_probability(img, 0)
for j in range(1, class_num):
probability = calculate_probability(img, j)
if max_probability < probability:
max_label = j
max_probability = probability
predict.append(max_label)
return np.array(predict)
# MNIST数据集有10种labels，分别为“0，1,2，3,4,5,6,7,8,9
class_num = 10
feature_len = 784
if __name__ == '__main__':
time_1 = time.time()
train_X, test_X, train_y, test_y = load_data()
prior_probability, conditional_probability = Train(train_X, train_y)
test_predict = Predict(test_X, prior_probability, conditional_probability)
score = accuracy_score(test_y, test_predict)
print(score)
需要数据的去我的GitHub上拿，地址：https://github.com/LeBron-Jian/MachineLearningNote
Sklearn实战三（高斯朴素贝叶斯）
代码：
from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# 读取数据
X = []
Y = []
fr = open("datingTestSet.txt", encoding='utf-8')
print(fr)
index = 0
for line in fr.readlines():
# print(line)
line = line.strip()
line = line.split('\t')
X.append(line[:3])
Y.append(line[-1])
# 归一化
scaler = MinMaxScaler()
# print(X)
X = scaler.fit_transform(X)
# print(X)
# 交叉分类
train_X, test_X, train_y, test_y = train_test_split(X, Y, test_size=0.2)
#高斯贝叶斯模型
model = GaussianNB()
model.fit(train_X, train_y)
# 预测测试集数据
predicted = model.predict(test_X)
# 输出分类信息
res = metrics.classification_report(test_y, predicted)
# print(res)
# 去重复，得到标签类别
label = list(set(Y))
# print(label)
# 输出混淆矩阵信息
matrix_info = metrics.confusion_matrix(test_y, predicted, labels=label)
# print(matrix_info)
需要数据的去我的GitHub上拿，地址：https://github.com/LeBron-Jian/MachineLearningNote
参考文献：https://www.cnblogs.com/pinard/p/6069267.html
https://www.cnblogs.com/youngsea/p/9327972.html
https://blog.csdn.net/qq_35044025/article/details/79322169
