python常用算法学习(3)——排序查找
完整代码及其数据,请移步小编的GitHub
传送门:请点击我
如果点击有误:https://github.com/LeBron-Jian/BasicAlgorithmPractice
1,什么是算法的时间和空间复杂度
算法(Algorithm)是指用来操作数据,解决程序问题的一组方法,对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但是在过程中消耗的资源和时间却会有很大的区别。
那么我们应该如何去衡量不同算法之间的优劣呢?
主要还是从算法所占用的时间和空间两个维度取考量。
- 时间维度:是指执行当前算法所消耗的时间,我们通常使用时间复杂度来描述。
- 空间维度:是指执行当前算法需要占用多少内存空间,我们通常用空间复杂度来描述
因此,评价一个算法的效率主要是看它的时间复杂度和空间复杂度情况,然而,有的时候时间和空间却又是鱼与熊掌,不可兼得,那么我们就需要从中去取一个平衡点。
下面分别学习一下时间复杂度和空间复杂度的计算方式。
1.1 时间复杂度
我们想要知道一个算法的时间复杂度,很多人首先想到的方法就是把这个算法程序运行一遍,那么它所消耗的时间就自然而然的知道了。这种方法可以吗?当然可以,不过它也有很多弊端。
这种方式非常容易受运行环境的影响,在性能高的机器上跑出来的结果与在性能低的机器上跑的结果相差会很大。而且对测试时使用的数据规模也有很大关系。再者我们再写算法的时候,还没有办法完整的去运行呢,因此,另一种更为通用的方法就出来了:大O符号表示法,即T(n) = O(f(n))。
我们先看一个例子:
for(i=1; i<=n; ++i)
{
j = i;
j++;
}
通过大O符号表示法,这段代码的时间复杂度为O(n),为什么呢?
在大O符号表示法中,时间复杂度的公式是:T(n) = O( f(n) ),其中f(n)表示每行代码执行次数之和,而O表示正比例关系,这个公式的全称是:算法的渐进时间复杂度。
我们继续看上面的例子,假设每行代码的执行时间都是一样的,我们用1颗粒时间来表示,那么这个例子的第一行耗时是1个颗粒时间,第三行的执行时间是n个颗粒时间,第四行执行时间也是n个颗粒时间(第二行和第五航是符号,暂时忽略),那么总时间就是1颗粒时间+n颗粒时间+n颗粒时间,即 T(n) = (1+2n)*颗粒时间,从这个结果可以看出,这个算法的耗时是随着n的变化而变化,因此,我们可以简化的将这个算法的时间复杂度表示为:T(n) = O(n)。
为什么可以这么去简化呢,因为大O符号表示法并不是用于来真实代表算法的执行时间的,它是用来表示代码执行时间的增长变化趋势的。
所以上面的例子中,如果n无限大的时候,T(n) = time(1+2n)中的常量1就没有意义了,倍数2也意义不大。因此直接简化为T(n) = O(n) 就可以了。
常用的时间复杂度量级有:
- 常数阶O(1)
- 对数阶O(N)
- 线性阶O(logN)
- 线性对数阶O(nlogN)
- 平方阶O(n2)
- 立方阶O(n3)
- K 次方阶O(n^k)
- 指数阶(2^n)
从上之下依次的时间复杂度越来越大,执行的效率越来越低。
下面选取一些较为常用的来说一下。
1,常数阶O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1),如:
int i = 1; int j = 2; ++i; j++; int m = i + j;
上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
2,对数阶O(N)
for(i=1; i<=n; ++i)
{
j = i;
j++;
}
这段代码,for循环里面的代码会执行N遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
3,线性阶O(logN)
先看代码
int i = 1;
while(i<n)
{
i = i * 2;
}
从上面代码可以看到,在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2^n
也就是说当循环 log2^n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logn)
4,线性对数阶O(nlogN)
线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)。
就拿上面的代码加一点修改来举例:
for(m=1; m<n; m++)
{
i = 1;
while(i<n)
{
i = i *
5,平方阶O(n2)
平方阶O(n2)更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
举例:
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(n*n),即 O(n²)
如果将其中一层循环的n改成m,即:
for(x=1; i<=m; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
那它的时间复杂度就变成了 O(m*n)
6,立方阶O(n3)及K 次方阶O(n^k)
参考上面O(n2)去理解就好了,相当于三层n循环,其他的类似。
除此之外,其实还有 平均时间复杂度、均摊时间复杂度、最坏时间复杂度、最好时间复杂度 的分析方法,有点复杂,这里就不展开了。
1.2 空间复杂度
空间复杂度:用来评估算法内存占用大小的式子。
既然时间复杂度不是用来计算程序具体耗时的,那么我们也应该明白,空间复杂度也不是用来计算程序实际占用的空间的。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用S(N)来定义。
空间复杂度的表示方式与时间复杂度完全一样:
- 算法使用了几个变量:O(1)
- 算法使用了长度为 n 的一维列表: O(n)
- 算法使用了m 行 n 列的二维列表:O(mn)
空间复杂度比较常用的有:O(1),O(n),O(n2),我们来看看:
空间复杂度O(1)
如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可以表示为O(1)。
举例:
int i = 1; int j = 2; ++i; j++; int m = i + j;
代码中的i,j,m所分配的空间都不随着处理数据量变化,因此他的空间复杂度S(n) = O(1)
空间复杂度O(n)
我们先看一个代码:
int[] m = new int[n]
for(i=1; i<=n; ++i)
{
j = i;
j++;
}
这段代码中,第一行new了一个数组出来,这个数据占用的大小为n,这段代码的2~6行,虽然有循环,但是没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即S(n)=O(n)。
空间换时间:常会为了追求时间复杂度而牺牲空间复杂度。
1.3 如何简单快速的判断算法复杂度
快速判断算法复杂度(适用于绝大多数简单情况):
- 确定问题规模 n
- 循环减半过程 ——> logN
- k层关于 n 的循环——> nk
复杂情况:根据算法执行过程判断
2,常用的算法总结
2.1 递归
2.1.1 递归概念
递归的两个特点:1:,调用自身 2,结束条件
举个例子学习下面函数是不是递归:
# 这个是一个死递归,只调用自身,但是没有结束条件
def func1(x):
print(x)
func1(x-1)
# 这个是一个死递归,看似有结束条件,但是却无法结束
def func2(x):
if x > 0:
print(x)
func2(x+1)
# 这是一个递归函数,满足调用自身,并且有结束条件
def func3(x):
if x > 0:
print(x)
func3(x-1)
# 这个也是一个递归,但是和func3有区别
def func4(x):
if x > 0:
func4(x-1)
print(x)
func3和func4的区别是什么?
假设x为3,那么func3输出的结果为:3,2,1 而 func4输出的结果为: 1,2,3。
为了方便理解,我们利用如下图:
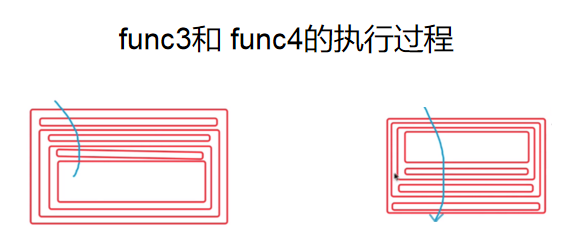
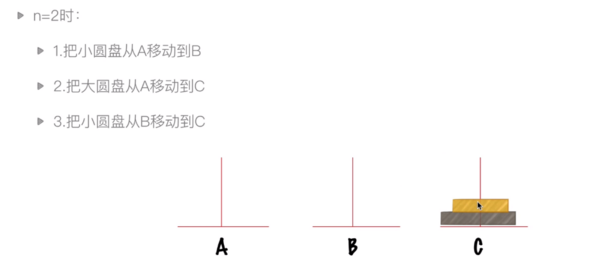
2.1.2 递归实例:汉诺塔问题
问题描述:大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从上往下按照大小顺序摞着64片黄金圆盘。大梵天命名婆罗门把圆盘从下面开始按大小顺序重新摆放在另一个柱子上。在小圆盘上不能放大圆盘,在三根柱子之间只能移动一个圆盘。64根柱子移动完毕之日,就是世界毁灭之时。
问题分析:
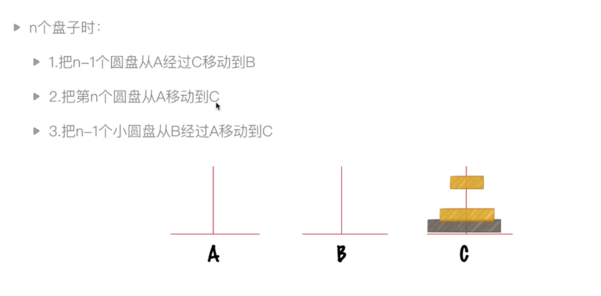
代码实现:
def hanoi(x,a,b,c):
if x>0:
# 除了下面最大的盘子,剩下的盘子从a移动到b
hanoi(x-1,a,c,b)
# 把最大的盘子从a移到c
print('%s->%s'%(a,c))
# 把剩余的盘子从b移到c
hanoi(x-1,b,a,c)
hanoi(3,'A','B','C')
# 计算次数
def cal_times(x):
num = 1
for i in range(x-1):
# print(i)
num = 2*num +1
print(num)
cal_times(3)
递归总结:
- 1,汉诺塔移动次数的递推式: h(x) = 2h(x-1)+1
- 2,h(64) = 18446744073709551615
- 3,假设婆罗门每秒钟搬一个盘子,则总共需要 5800亿年
证明:为什么汉诺塔的计算次数是2n+1呢?
对于一个单独的塔,可以进行以下操作:
- 1:将最下方的塔的上方的所有塔移动到过渡柱子
- 2:将底塔移动到目标柱子
- 3:将过渡柱子上的其他塔移动到目标柱子
所以f(3)=f(2)+1+f(2)=7
然后以此类推
- f(4)=f(3)+1+f(3)=15
- f(5)=f(4)+1+f(4)=31
- f(6)=f(5)+1+f(5)=63
- f(7)=f(6)+1+f(6)=127
- f(8)=f(7)+1+f(7)=255
- f(9)=f(8)+1+f(8)=511
f(x+1)=2*f(x)+1
再进一步,可以得到通项公式为
f(x)=2^x-1
2.2 查找算法
查找:在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程。
列表查找(线性表查找):从列表中查找指定元素
- 输入:列表,待查找元素
- 输出:元素下标(未找到元素时一般返回None或 -1)
内置列表查找函数:index()
2.2.1 顺序查找(Linear Search)
顺序查找:也叫线性查找,从列表第一个元素开始,顺序进行搜索,直到找到元素或搜索到列表最后一个元素为止。
时间复杂度为:O(n)
def linear_search(data_set, value):
for i in data_set:
if value == data_set[i]:
return i
return None
2.2.2 二分查找(Binary Search)
二分查找:又叫折半查找,从有序列表的初始候选区 li[0:n] 开始,通过对待查找的值与候选区中间值得比较,可以使候选区减少一半。
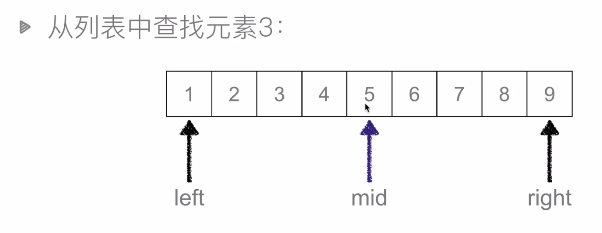
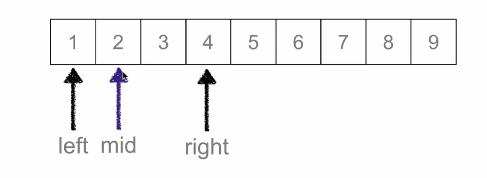
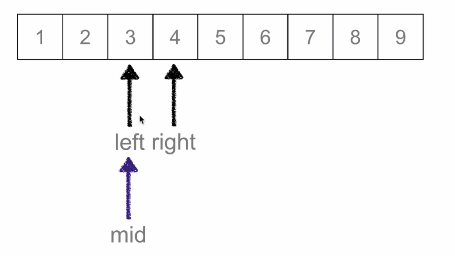
时间复杂度:O(logN)
def binary_search(data_list, val):
low = 0 # 最小数下标
high = len(data_list) - 1 # 最大数下标
while low <= high:
mid = (low + high) // 2 # 中间数下标
if data_list[mid] == val: # 如果中间数下标等于val, 返回
return mid
elif data_list[mid] > val: # 如果val在中间数左边, 移动high下标
high = mid - 1
else: # 如果val在中间数右边, 移动low下标
low = mid + 1
else:
return None # val不存在, 返回None
ret = binary_search(list(range(1, 10)), 3)
print(ret)
2.3 列表排序算法
排序:将一组“无序”的记录序列调整为“有序” 的记录序列。
列表排序:将无序列表变为有序列表
- 输入:列表
- 输出:有序列表
升序与降序
内置排序算法:sort()
2.3.1 常见排序算法
如下图所示:

部分排序算法的时间复杂度和空间复杂度及其稳定性如下:
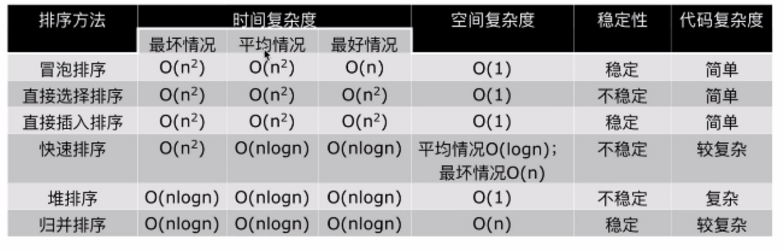
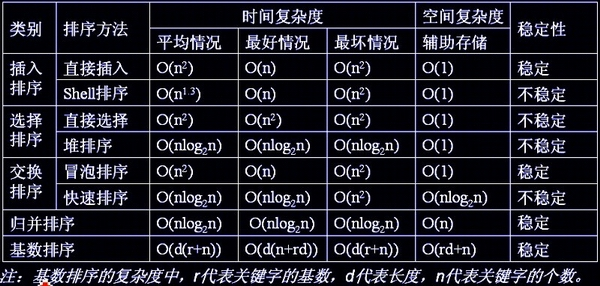
2.3.2 冒泡排序(Bubble Sort)
冒泡排序:像开水烧气泡一样,把最大的元素冒泡到最上面。一趟就是把最大的冒到最上面。冒到最上面的区域叫有序区。下面叫无序区。
列表每两个相邻的数,如果前面比后面大,则交换这两个数。
一趟排序完成后,则无序区减少一个数,有序区增加一个数。
代码关键点:趟,无序区范围
时间复杂度:O(n2)
def bubble_sort(li):
for i in range(len(li)-1):
for j in range(len(li)-1-i):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
return li
冒泡排序降序排列:
# 降序排列
import random
def bubble_sort(li):
for i in range(len(li)-1): # 第 i 趟
for j in range(len(li)-1-i):
if li[j] < li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
li = [random.randint(0, 10) for i in range(10)]
print(li)
bubble_sort(li)
print(li)
'''
[5, 2, 10, 5, 5, 2, 5, 4, 3, 2]
[10, 5, 5, 5, 5, 4, 3, 2, 2, 2]
'''
当然也可以打印每一趟,看看冒泡排序的过程:
# 升序排列,打印每一趟,看看其过程
def bubble_sort(li):
for i in range(len(li)-1): # 第 i 趟
for j in range(len(li)-1-i):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
print(li)
li = [9,8,7,6,5,4,3,2,1]
print('origin:',li)
bubble_sort(li)
'''
origin: [9, 8, 7, 6, 5, 4, 3, 2, 1]
[8, 7, 6, 5, 4, 3, 2, 1, 9]
[7, 6, 5, 4, 3, 2, 1, 8, 9]
[6, 5, 4, 3, 2, 1, 7, 8, 9]
[5, 4, 3, 2, 1, 6, 7, 8, 9]
[4, 3, 2, 1, 5, 6, 7, 8, 9]
[3, 2, 1, 4, 5, 6, 7, 8, 9]
[2, 1, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]
'''
冒泡排序的最差情况,即每次都交互顺序的情况下,时间复杂度为O(n**2)。
存在一个最好情况就是列表本来就是排好序,所以可以加一个优化,也就是一个标志位,如果冒泡排序中的一趟排序没有出现交换的情况,说明列表已经有序,可以直接结束算法,则直接return。
def optimize_bubble_sort(li):
for i in range(len(li)-1):
exchange = False
for j in range(len(li)-1-i):
if li[j] > li[j+1]:
li[j],li[j+1] = li[j+1],li[j]
exchange =True
if not exchange:
return li
return li
origin_list = [9,8,7,6,5,4,3,2,1]
print('origin_list:', origin_list)
res = optimize_bubble_sort(origin_list)
print(res)
# origin_list: [9, 8, 7, 6, 5, 4, 3, 2, 1]
# [1, 2, 3, 4, 5, 6, 7, 8, 9]
2.3.3 选择排序(Select Sort)
一趟排序记录最小的数,放到第一个位置
再一趟排序记录记录列表无序区最小的数,放到第二个位置。。。。
算法的关键点:有序区和无序区,无序区最小数的位置。
先看一个简单的选择排序
def select_sort_simple(li):
li_new = []
for i in range(len(li)):
min_val = min(li)
li_new.append(min_val)
li.remove(min_val)
return li_new
li = [4,3,2,1]
print(select_sort_simple(li))
# [1, 2, 3, 4]
我们会发现首先他生成了两个列表,那么就占用了两份内存,而算法的思想则是能省则省,能抠则抠,所以我们需要改进一下。
def select_sort(li):
for i in range(len(li)-1): # i 是第几趟
min_loc = i
for j in range(i+1, len(li)):
if li[j] < li[min_loc]:
min_loc = j
li[i], li[min_loc] = li[min_loc], li[i]
return li
li = [1,2,3,4]
print(select_sort(li))
# [1, 2, 3, 4]
2.3.4 插入排序(Insertion Sort)
原理:把列表分成有序区和无序区两个部分。最初有序区只有一个元素。然后每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
def insert_sort(li):
for i in range(1, len(li)): # i表示摸到的牌的下标
temp = li[i]
j = i - 1 # j指的时手里的牌的下标
# if j > 0 and temp < li[j]: # 找到一个合适地位置插进去
while j >= 0 and li[j] > temp:
li[j + 1] = li[j]
j -= 1
li[j + 1] = temp
return li
简单形象的一张图:

时间复杂度是 O(n2)
如果目标是 n 个元素的序列升序排列,那么采用插入排序存在最好情况和最坏的情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需要(n-1)次即可。最坏的情况就是序列是降序排列,那么此时需要进行的比较共有 n(n-1)/2次。插入排序的赋值操作时比较操作的次数加上 (n-1)次。平均来说插入排序算法的时间复杂度为O(n^2),因而插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如量级小于千,那么插入排序还是一个不错的选择。
2.3.5 快速排序
原理:让指定的元素归位,所谓归位,就是放到他应该放的位置(左边的元素比他小,右边的元素比他大),然后对每个元素归位,就完成了排序。
可以参考下面动图来理解代码:
左边空位置,从右边找,右边空位置,从左边找。当左边和右边重合的时候,就是mid。

下图来自百度百科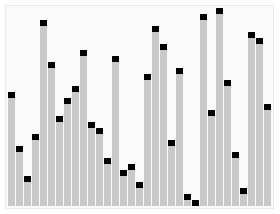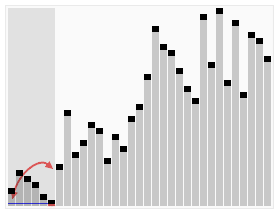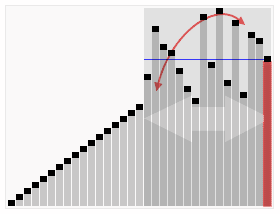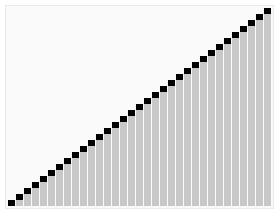
快速排序——框架函数
def quick_sort(data, left, right):
if left < right:
mid = partition(data, left, right)
quick_sort(data, left, mid-1)
quick_sort(data, mid+1, right)
完整代码如下:
def partition(data, left, right):
# 把左边第一个元素赋值给tmp,此时left指向空
tmp = data[left]
# 如果左右两个指针不重合,则继续
while left < right:
while left < right and data[right] >= tmp:
right -= 1 # 右边的指标往左走一步
# 如果right指向的元素小于tmp,就放到左边目前为空的位置
data[left] = data[right]
print('left:', li)
while left < right and data[left] <= tmp:
left += 1
# 如果left指向的元素大于tmp,就交换到右边目前为空的位置
data[right] = data[left]
print('right:', li)
data[left] = tmp
return left
# 写好归位函数后,就可以递归调用这个函数,实现排序
def quick_sort(data, left, right):
if left < right:
# 找到指定元素的位置
mid = partition(data, left, right)
# 对左边的元素排序
quick_sort(data, left, mid - 1)
# 对右边的元素排序
quick_sort(data, mid + 1, right)
return data
li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
print('start:', li)
partition(li, 0, len(li) - 1)
print('end:', li)
'''
start: [5, 7, 4, 6, 3, 1, 2, 9, 8]
left: [2, 7, 4, 6, 3, 1, 2, 9, 8]
right: [2, 7, 4, 6, 3, 1, 7, 9, 8]
left: [2, 1, 4, 6, 3, 1, 7, 9, 8]
right: [2, 1, 4, 6, 3, 6, 7, 9, 8]
left: [2, 1, 4, 3, 3, 6, 7, 9, 8]
right: [2, 1, 4, 3, 3, 6, 7, 9, 8]
end: [2, 1, 4, 3, 5, 6, 7, 9, 8]
'''

正常的情况,快排的复杂度是O(nlogn)
快排存在一个最坏情况,就是每次归位,都不能把列表分成两部分,此时复杂度就是O(n2)了,如果要避免设计成这种最坏情况,可以在取第一个数的时候不要取第一个了,而是取一个列表中的随机数。
2.3.6 堆排序(Heap Sort)
堆排序用在一些非常经典的经常,下面我们学习一下堆相关内容,最开始我们从堆的底层实现和实际应用举例开始来了解堆这种数据结构的用途,因为只有知道了某个东西的实际用途再来深入学习这样东西才会更有方向感。
堆本质是使用大根堆或小根堆来对一个数组进行排序。所以首先要理解树的概念。
关于树的理解请参考博客:https://www.cnblogs.com/wj-1314/p/11631934.html
堆的底层实现
堆简单来说:一种特殊的完全二叉树结构
- 大根堆:一种完全二叉树,满足任一节点都比其孩子节点大
- 小根堆:一种完全二叉树,满足任一节点都比其孩子节点小
堆是用数组来存储的,但是我们在对堆进行操作的时候实际上是将其看成并构建成一颗完全二叉树,之所以用数组来存储是因为完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的,因为我们不需要像构建二叉树节点那样花费内存空间来存储每个节点的左右子节点,可以通过数组下标就直接找到一个节点的左右子节点和父节点,我们画图来理解一下:
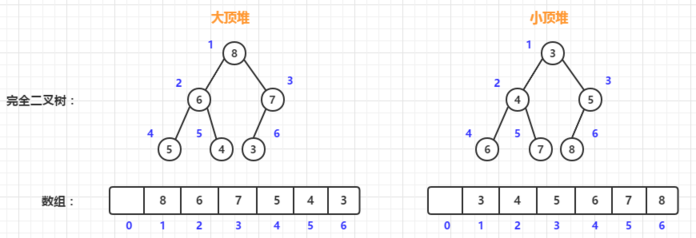
上图就是大根堆和小根堆,这也是堆的两种实现方式,通过图可以很好地理解大根堆和小根堆,大根堆中根节点存储的是集合中最大的元素,它的左右孩子都小于它,同时左右子树也是遵循这样的规律,小根对中根节点存储的是集合中最小的元素,它的左右孩子都小于它,同样左右子树也遵循,堆的操作比如插入删除也正是维护这样的一种关系特性。
堆排序——堆的向下调整性质
假设根节点的左右子树都是堆,但根节点不满足堆的性质,可以通过一次向下的调整来将其变成一个堆
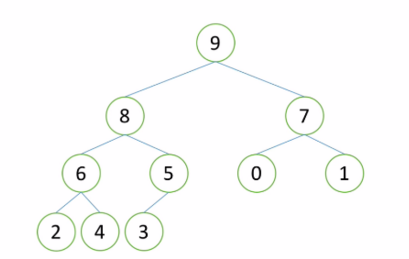
当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆。
堆的插入操作
首先我们要明白的是对堆进行数据的插入和删除都需要满足堆的两个特性,对于我们插入新的节点数据,其实就是在数组的尾部进行添加,这样自然会满足堆所构建的完全二叉树结构不会被破坏,但是插入新数据后可能就不满足堆中父亲节点和左右孩子的大小关系了,所以插入新的数据后都需要进行堆化(heapify)操作,堆化有两种形式,一种是从下往上,另一种是从上往下,在插入操作的时候我们很快就会明白肯定是从下往上的,我们具体看什么是堆化的过程:
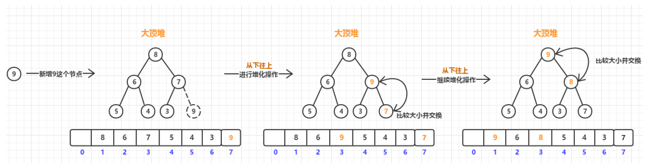
可以看到堆化操作其实很简单,就是看新增的这个节点和父亲节点的大小关系,在大根堆中如果新增的节点比父亲节点大就和父亲节点替换位置,然后继续向上直到小于父亲节点或到达根节点时结束,可以看出在插入新数据经过堆化操作之后就满足了堆的特性,这也就是在插入元素的全部过程。
堆的删除操作
我们知道堆分为大顶堆和小根堆,也就是堆顶元素就是集合中最大或者最小的元素,我们一样拿大顶堆来说,当我们删除元素的时候就是删除堆顶的最大值的元素,我们看下如果我们粗暴的将堆顶删除然后从左右子孩子中选一个最大的进行填补,直到叶子节点这种方式会有什么问题,用下图看:
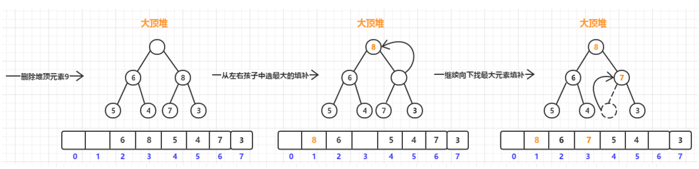 有没有发现这种方式最后导致堆不是一个完全二叉树了?所以这种删除方式是行不通的,正确的思路就是将数组中的最后一个元素放到堆顶进行覆盖,然后丢掉数组末尾的元素,这个时候还没结束,你很快就会想到次数的堆是不满足父亲节点的值大于(小于)左右子孩子(同样左右子树也遵循),这个时候就要进行从上往下的堆化操作,我们一样用图来分析整个过程:
有没有发现这种方式最后导致堆不是一个完全二叉树了?所以这种删除方式是行不通的,正确的思路就是将数组中的最后一个元素放到堆顶进行覆盖,然后丢掉数组末尾的元素,这个时候还没结束,你很快就会想到次数的堆是不满足父亲节点的值大于(小于)左右子孩子(同样左右子树也遵循),这个时候就要进行从上往下的堆化操作,我们一样用图来分析整个过程:
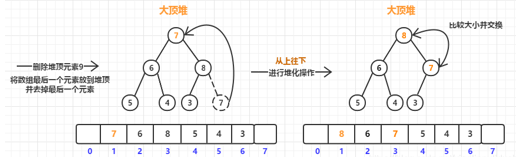
同样根据图的整个过程发现删除元素也是非常简单的,两个大步骤:1,将数组末尾元素替换掉堆顶元素,然后去掉末尾的元素;2,进行从上往下的堆化操作,也就是拿当前堆顶元素与大于本元素的其中最大的那个孩子节点进行位置替换,同样直到均小于等于左右孩子节点或者到达叶子节点结束。
堆排序过程
1,建立堆
2,得到堆顶元素,为最大元素
3,去掉堆顶,将堆最后一个元素放到堆顶,此时可以通过一次调整重新使堆有序。
4,堆顶元素为第二大元素
5,重复步骤3,直到堆变为空
代码如下:
def sift(data, low, high):
i = low
j = 2*i+1
tmp = data[i]
while j <=high:
if j < high and data[j] < data[j+1]:
j+=1
if tmp < data[j]:
data[i] = data[j]
i = j
j = 2*i+1
else:
break
data[i] = tmp
def heap_li(li):
n = len(li)
for i in range((n - 2) // 2, -1, -1):
# i表示建堆的时候调整的部分的跟的下标
sift(li, i, n - 1)
# 建堆完成了
print('建堆完成后的列表:',li)
for i in range(n-1, -1, -1):
# i 指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0]
sift(li, 0, i-1) # i-1是新的high
print(li)
li = [i for i in range(12)]
import random
random.shuffle(li)
print(li)
heap_li(li)
print(li)
'''
[7, 2, 4, 3, 8, 9, 0, 5, 11, 6, 10, 1]
建堆完成后的列表: [11, 10, 9, 5, 8, 4, 0, 2, 3, 6, 7, 1]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
'''
Python标准库模块——heapq
(参考地址:https://docs.python.org/zh-cn/3.8/library/heapq.html)
该模块提供了堆排序算法的实现。堆是二叉树,最大堆中父节点大于或等于两个子节点,最小堆父节点小于或等于两个子节点。为了方便比较,不存在的元素被认为是无限大,堆最有趣的特性在于最小的元素总是在根节点:heap[0]。
创建堆:heapq 有两种方式创建堆,一种是使用一个空列表,然后使用 heapq.heappush() 函数把值加入堆中,另一种就是使用 heap.heapify(list)转换列表为堆结果。
下面看看定义以下函数:
- heapq.heappush(heap, item):将item的值加入 heap中,保持堆的不变性
- heapq.heappop(heap):弹出并返回heap的最小的元素,保持堆的不变性。如果堆为空,抛出IndexError,使用 heap[0],可以只访问最小的元素而不弹出它
- heapq.heappushpop(heap, item):将 item 放入堆中,然后弹出并返回 heap的最小元素,该组合操作比先调用heappush(),再调用 heappop() 运行起来更有效率
- heapq.heapify(x):将list x 转换成堆,原地,线性时间内
创建的代码如下:
import heapq
# 第一种方法——建立堆
nums = [2, 3, 5, 1, 32, 42, 422]
heap = []
for num in nums:
# 加入堆
heapq.heappush(heap, num)
# 如果只是想获取最小值而不是弹出,使用 heap[0]
print(heap[0])
# 获取堆排序结果
res = [heapq.heappop(heap) for _ in range(len(nums))]
print(res)
'''
1
[1, 2, 3, 5, 32, 42, 422]
'''
# 第二种方法——建立堆
nums = [2, 3, 5, 1, 32, 42, 422]
heapq.heapify(nums)
# 获取堆排序结果
res = [heapq.heappop(nums) for _ in range(len(nums))]
print(res[0])
print(res)
# 1
# [1, 2, 3, 5, 32, 42, 422]
堆排序应用——topK问题
通过学习堆的底层实现之后,我们已经初步了解堆这种的数据结构,我们根据上面堆的结构特性来分析一下具体用途
问题描述:现在有n个数,设计算法得到前k大的数( k<n)
求Topk问题,比如我们要获取Top 100的排行榜,热搜词等等问题,拿Top热搜词来说,大致的实现思路就是我们先得到存储所有词的出现次数,然后维护一个大小 100 的小根堆,堆顶是当前统计的集合中排行最小的,如果我们新来的词出现的次数比堆顶还小直接抛弃,如果比堆顶大我们就尝试插入到堆中,插入的过程中还没达到最大容量的话就插入,容量达到最大的话就抛弃堆顶元素替换掉堆顶(当然这里还要进行堆结构的维护),遍历到最终小根堆中保存的就是所有词中出现次数最多的前100个热搜词。
解决思路:
- 排序后切片 时间复杂度为:O(nlogn)
- 排序(选择,插入,冒泡) 时间复杂度为:O(mn)
- 堆排序思路 时间复杂度为:O(mlogn)
代码如下:
def sift(li, low, high):
i = low
j = 2 * i + 1
tmp = li[low]
while j <= high:
if j + 1 <= high and li[j + 1] < li[j]:
j = j + 1
if li[j] < tmp:
li[i] = li[j]
i = j
j = 2 * j + 1
else:
break
li[i] = tmp
def topk(li, k):
heap = li[0:k]
for i in range((k - 2) // 2, -1, -1):
sift(heap, i, k - 1)
# 1,建堆
for i in range(k, len(li) - 1):
if li[i] > heap[0]:
heap[0] = li[i]
sift(heap, 0, k - 1)
# 2,遍历
for i in range(k - 1, -1, -1):
heap[0], heap[i] = heap[i], heap[0]
sift(heap, 0, i - 1)
# 3,出数
return heap
import random
li = list(range(1000))
random.shuffle(li)
print(topk(li, 10))
2.3.7 归并排序(Merge Sort)
归并:假设现在的列表分两段有序,如何将其合成为一个有序列表,这种操作叫做一次归并。
如下图所示:虚线分开,两个箭头分别指向列表的第一个元素。然后从左边开始比较两边的元素,小的出列。然后继续循环,这样就排出来一个有序列表。
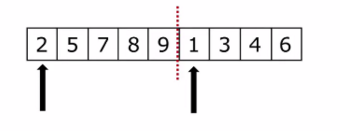
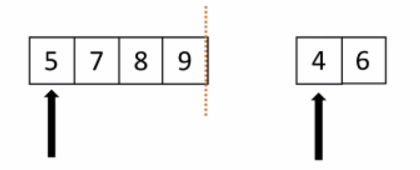
应用到排序就是把列表分成一个元素一个元素的,一个元素当然是有序的,将有序列表一个一个合并,列表越来越大,最终合并成一个有序的列表。
归并排序如图所示:
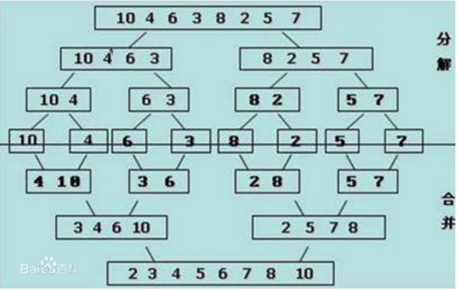
归并排序代码如下:
def merge(li, low, mid, high):
i = low # i为左边列表开头元素的坐标
j = mid + 1 # j为右边列表开头元素的坐标
ltmpd = [] # 临时列表
# 只要两边都有数
while i <= mid and j <= high:
if li[i] < li[j]:
ltmpd.append(li[i])
i += 1
else:
ltmpd.append(li[j])
j += 1
# while执行完,肯定有一部分没数字了,就是两个箭头肯定有一个指向没数了
while i <= mid:
ltmpd.append(li[i])
i += 1
while j <= high:
ltmpd.append(li[j])
j += 1
li[low:high + 1] = ltmpd
# return ltmpd
def merge_sort(li, low, high):
if low < high: # 列表中至少两个元素,递归
mid = (low + high) // 2
merge_sort(li, low, mid)
merge_sort(li, mid + 1, high)
merge(li, low, mid, high)
li = list(range(10))
import random
random.shuffle(li)
print(li)
merge_sort(li, 0, len(li)-1)
print(li)
归并排序的时间复杂度:O(nlogn)
归并排序的空间复杂度:O(n)
2.3.8 快速排序,堆排序,归并排序三种算法的总结
1,三种排序算法的时间复杂度都是O(nlogn)
2,一般情况下,就运行时间而言:快速排序 < 归并排序 < 堆排序
3,三种排序算法的缺点
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
2.3.9 希尔排序(Shell Sort)
希尔排序(Shell Sort)是一种分组插入排序算法。
其算法步骤如下:
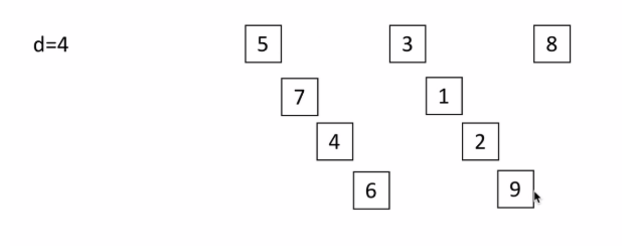
- 首先取一个整数 d1=n/2,将元素分为 d1个组,每组相邻量元素之间距离为 d1,在各组内进行直接插入排序;
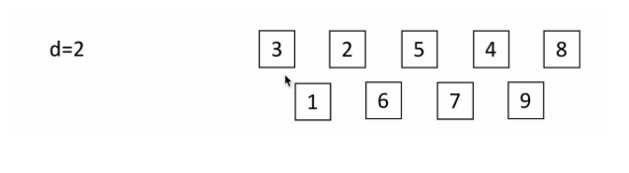
- 然后取第二个整数 d2=d1/2,重复上述分组排序过程,知道 di=1,即所有元素在同一组内进行直接插入排序;
- 最后希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序,最后一趟排序使得所有数据有序
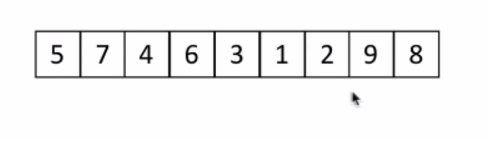
图解如下:
1,数组(列表)如下:
2,d=4(即d=len(li)/2):
3,d=2:
4,d=1:

在wiki查找地址如下:https://en.wikipedia.org/wiki/Shellsort#Gap_sequences
希尔排序的时间复杂度讨论比较复杂,并且和选取的gap序列有关。
2.3.10 计数排序(Count Sort)
简单来说如下图所示:
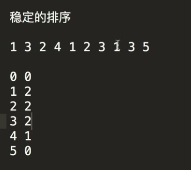
出现那个数,就给那个数的数量加一。
代码如下:
def count_sort(li, max_count=100):
count = [0 for _ in range(max_count+1)]
for val in li:
count[val] += 1
li.clear() # 原列表清空,这样就不用建新列表,省内存
for ind, val in enumerate(count):
for i in range(val):
li.append(ind)
import random
li = [random.randint(0, 19) for _ in range(30)]
print(li)
count_sort(li)
print(li)
'''
[1, 4, 13, 6, 19, 4, 9, 14, 10, 15, 7, 1, 1, 9, 3, 8, 17, 3, 18, 1, 8, 17, 14, 2, 10, 0, 5, 8, 12, 15]
[0, 1, 1, 1, 1, 2, 3, 3, 4, 4, 5, 6, 7, 8, 8, 8, 9, 9, 10, 10, 12, 13, 14, 14, 15, 15, 17, 17, 18, 19]
'''
对列表进行排序,已知列表中的数范围都在0到100之间,设计时间复杂度为O(n)的算法。就可以使用此算法,即使列表长度大约为100万,虽然列表长度很大,但是数据量很小,会有大量的重复数据,我们可以考虑对这100个数进行排序。
2.3.11 桶排序(Bucket Sort)
桶排序也叫计数排序,简单来说,就是将数据集里面所有元素按顺序列举出来,然后统计元素出现的次数,最后按照顺序输出数据集里面的元素。
在计数排序中,如果元素的范围比较大(比如在1到1亿之间),如何改造算法?
桶排序(Bucket Sort):首先将元素分在不同的桶中,在对每个桶中的元素排序。
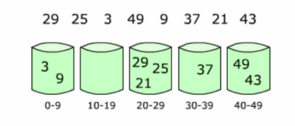
如上图,列表为 [29, 25, 3, 49, 9, 37, 21, 43]排序,我们知道数组的范围是0~49,我们将其分为5个桶,然后放入数字,一次对桶中的元素排序。
桶排序的表现取决于数据的分布。也就是需要对不同数据排序采取不同的分桶策略。
- 平均情况时间复杂度为:O(n+k)
- 最坏情况时间复杂度为:O(n2k)
- 空间复杂度为:O(nk)
代码如下:
#_*_coding:utf-8_*_
def bucket_sort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶
for var in li:
# 0 -》 0, 86
i = min(var // (max_num // n), n-1) # i表示var放到几号桶里
buckets[i].append(var) # 把var加入到桶里
# [0, 2, 4]
# 保持桶内的顺序
for j in range(len(buckets[i])-1, 0, -1):
if buckets[i][j] < buckets[i][j-1]:
buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j]
else:
break
sorted_li = []
for buc in buckets:
sorted_li.extend(buc)
return sorted_li
import random
if __name__ == '__main__':
li = [random.randint(0, 10000) for i in range(10000)]
# print(li)
li = bucket_sort(li)
print(li)
2.3.12 基数排序
多关键字排序:加入现在有一个员工表,要求按照薪资排序,年龄相同的员工按照年龄排序。
方法:先按照年龄进行排序,再按照薪资进行稳定的排序。
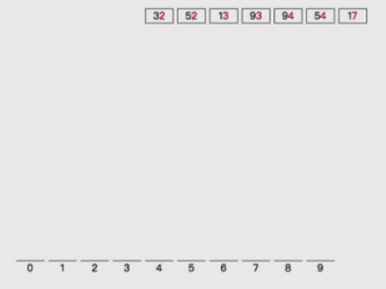
比如对 [32, 13, 94, 52, 17, 54, 93] 排序是否可以看成多关键字排序?
实现示例如下:
1,首先按照个位分桶:
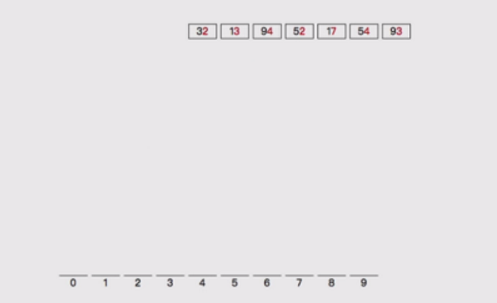
2,按照个位数分好,桶,然后摆回原位
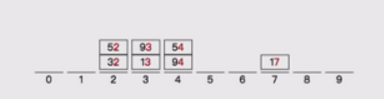
3,按照十位数进行分桶,然后将桶里的数排序
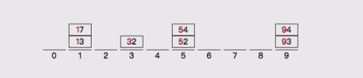
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按照每个位数分别比较。由于整数也可以表达字符串(比如名称或日期)和特定格式的浮点数,所以基础排序也不是只能使用于整数。
基数排序的时间复杂度为:O(kn)
基数排序的空间复杂度为:O(k+n)
基数排序中 k 表示数字位数
由于基数排序使用了桶排序,所以空间复杂度和桶排序的空间复杂度是一样的。
代码如下:
def list_to_buckets(li, base, iteration):
buckets = [[] for _ in range(base)]
for number in li:
digit = (number // (base ** iteration)) % base
buckets[digit].append(number)
return buckets
def buckets_to_list(buckets):
return [x for bucket in buckets for x in bucket]
def radix_sort(li, base=10):
maxval = max(li)
it = 0
while base ** it <= maxval:
li = buckets_to_list(list_to_buckets(it, base, it))
it += 1
return li
2.3.13 基数排序 VS 计数排序 VS 桶排序
这三种排序算法都利用了桶的概念,但对于桶的使用方法上有明显差异。
- 基数排序:根据键值的每位数字来分配桶
- 计数排序:每个桶只存储单一键值
- 桶排序:每个桶存储一定范围内的数值
三,几道查找排序习题
这一节是对前面学习的算法的应用,也就是习题练习。
1,给两个字符串s和t,判断 t是否为s的重新排列后组成的单词
s = 'anagram' t='nagaram' return true
s='rat', t='car', return false
两种方法一种直接使用Python的list排序,当然这种时间复杂度可能高一些。另一种方法使用字典记录list中出现字母的次数。代码如下:
def isAnagram0(s, t):
return sorted(list(s)) == sorted(list(t))
def isAnagram1(s, t):
dict1 = [] # ['a':1, 'b':2]
dict2 = []
for ch in s:
dict1[ch] = dict1.get(ch, 0) + 1
for ch in t:
dict2[ch] = dict2.get(ch, 0) + 1
return dict1 == dict2
2,给定一个 m*n 的二维列表,查找一个数是否存在,列表有下列特性:
-
每一行的列表从左到右已经排序好
-
每一行第一个数比上一行最后一个数大

思路如下:有两个方法,第一个是暴力遍历法,但是这种时间复杂度会很高,而相对来说改进的方法是二分查找。
实现代码如下:
def searchMatrix(matrix, target):
for line in matrix:
if target in line:
return True
return False
def searchMatrix1(matrix, target):
h = len(matrix)
if h == 0:
return False # h=0 即为 []
# 当然也出现一种可能就是 [[],[]]
w = len(matrix[0])
if w == 0:
return False
left = 0
right = w * h - 1
# 直接使用二分查找的代码
while left <= right:
mid = (left + right) // 2
i = mid // w
j = mid % w
if matrix[i][j] == target:
return True
elif matrix[i][j] > target:
right = mid - 1
else:
left = mid + 1
else:
return False
matrix = [[1, 2, 3], [5, 6, 7], [9, 12, 23]]
target = 32
res = searchMatrix1(matrix, target)
print(res)
3,给定一个列表和一个整数,设计算法找到两个数的下标,使得两个数之和为给定的整数。保证肯定仅有一个结果。例如,列表[1,2,5,4] 与目标整数3,1+2=3,结果为(0,1)
代码如下:
def TwoSum(nums, target):
'''
:param nums: nums是代表一个list
:param target: target是一个数
:return: 结果返回的时两个数的下标
'''
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[i] + nums[j] == target:
return (i, j)
def TwoSum1(nums, target):
# 新建一个空字典用来保存数值及在其列表中对应的索引
dict1 = {}
for i in range(len(nums)):
# 相减得到另一个数值
num = target - nums[i]
if num not in dict1:
dict1[nums[i]] = i
# 如果在字典中则返回
else:
return [dict1[num], i]
def binary_search(li,left, right, val):
while left <= right: # 候选区有值
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] < val:
left = mid +1
else:
right = mid -1
else:
return None
def TwoSum2(nums, target):
for i in range(len(nums)):
a = nums[i]
b = target - a
if b >=a:
j = binary_search(nums, i+1, len(nums)-1, a)
else:
j = binary_search(nums, 0, i-1, b)
return (i, j)



