带花树算法
题目描述
给定一张 $n$ 个点 $m$ 条边的无向简单图,求图的一个最大匹配。
输入格式
第一行两个正整数 $n, m$ ($2 \leq n \leq 500; 1 \leq m \leq \dbinom n2$),表示图的边数和点数。
接下来 $m$ 行,每行两个整数 $u, v$ ($1 \leq u, v \leq n; u \neq v$),表示 $u$ 到 $v$ 之间有一条边相连,保证同一条边不会出现两次。
输出格式
第一行一个整数,表示最大匹配的大小。
接下来一行 $n$ 个整数,描述这个最大匹配。第 $v$ 个整数表示点 $v$ 在最大匹配中的匹配点,如果不存在输出 $0$。
题解
先来回忆一下二分图最大匹配时的几个概念:
交错路:对路径 $v_1 \xrightarrow {e_1} v_2 \xrightarrow {e_2} \cdots \xrightarrow {e_{n-1}} v_n$,如果匹配边和未匹配边交替出现,且当 $e_1$ 为非匹配边时 $v_1$ 为非匹配点,当 $e_{n-1}$ 为非匹配边时 $v_n$ 为非匹配点,这样的路径为交错路。
交错路的基本性质:将交错路中的所有边的匹配状态改变,所得的匹配还是一个合法匹配。
增广路:满足 $e_1$ 和 $e_{n-1}$ 均为非匹配边的交错路称为增广路,其中 $v_1$ 和 $v_n$ 称为增广路的端点。
增广路的基本性质:将增广路中的所有边的匹配状态改变,所得的匹配的大小比原匹配大小多 $1$。
增广路引理:对于一个匹配 $M$,如果不存在以点 $v$ 为端点的增广路,则存在一个最大匹配 $M'$,其中 $v$ 不为匹配点。(证明略,主要思路为取两个匹配的对称差 $M \oplus M'$)
可以发现,最大匹配中一定不存在增广路,那不存在增广路的匹配是否是最大匹配呢?
答案是肯定的,这就是增广路定理:匹配 $M$ 为最大匹配当且仅当 $M$ 中不存在增广路。
证明:(仅证充分性) 对匹配 $M$,设 $v$ 是未匹配点,由于不存在以 $v$ 为端点的增广路,由增广路引理,可得存在一个最大匹配,$v$ 不为匹配点,因此可以删去 $v$。重复操作直到所有的点都为匹配点,此时的匹配显然是 (删点后的) 图的最大匹配,由于删点过程中原图的最大匹配等于新图的最大匹配,因此 $M$ 就是原图的最大匹配。
可以发现,上述结论没有遇到二分图的性质。因此对于一般的图 $G$,它也是成立的。
因此,对于图的匹配问题,算法的流程就是这样的:
按顺序枚举每个点,寻找以它为端点的增广路径,如果找到了,就将它增广;如果找不到,由增广路引理,点 $v$ 就没有用了,枚举下一个点。由于增广的过程中匹配点不会变为非匹配点,因此我们只需按照顺序将各个点枚举一次,最终的匹配就是最大匹配。
现在问题是,如何寻找以给定点 $v$ 为端点的增广路径?
显然暴力搜索 (dfs) 的复杂度是 $O(V!)$ 的,太大了。我们考虑记忆化搜索,即如果一个点搜索过了,记录下它的信息,下次重复搜索的时候直接调用即可。
此时,如果 $G = (V_1, V_2; E)$ 为二分图,不妨设 $v \in V_1$,则增广路中匹配边一定是从 $V_2$ 到 $V_1$ 的边,非匹配边则一定从 $V_1$ 连向 $V_2$。
那么,如果在某次搜索中,$V_1$ 中的点 $u$ 找不到连出去的增广路,那么下一次到达点 $u$ 时下一步也需要为非匹配边,根据之前搜索的结果,也是找不到增广路的,因此不需要再去 $u$ 搜索。这样一来,每个点至多被访问到一遍,因此寻找增广路的复杂度就变成了 $O \left( \sum d(v) \right) = O(E)$ 的,总时间复杂度 $O \left( VE \right)$。
接下来考虑一般的图。一般图显然没有显式地分图策略,因此我们要在搜索 (dfs) 的过程中动态地为点分类。
我们将起点定义为 $B$ 类点,增广奇数次的点定义为 $G$ 类点,增广偶数次的点定义为 $B$ 类点。
由增广路的定义,从 $G$ 类点出发一定经过匹配边,故只需将它匹配的点定义为 $B$ 类点,加入队列/栈即可,非常简单。
而从 $B$ 类点出发,就需要枚举边了:首先显然不能枚举刚刚过来的匹配点 ($G$ 类点),其次,如果遇到了另一个 (找不到增广路的) $G$ 类点 $u$,那么如果把 $u$ 加入到增广路的话,那么根据之前搜索的结果,也是找不到增广路的,因此不需要把 $u$ 加入队列/栈。综上所述,我们有 (结论 1) 如果 $B$ 类点枚举到了 $G$ 类点,直接忽略。
如果遇到一个还没有分类的点 $u$,如果 $u$ 是非匹配点,那么由增广路的定义,$v \leadsto u$ 就是一条增广路,直接把它增广即可。即 (结论 2) 如果 $B$ 类点枚举到了非匹配点,说明已经找到增广路,直接增广即可。
反之,如果 $u$ 是匹配点,我们把 $u$ 归为 $G$ 类,由增广路的定义,我们需要经过匹配边,因此把 $u$ 的匹配点归为 $B$ 类,继续搜索。即 (结论 3) 如果 $B$ 类点枚举到了未分类的匹配点,将它归为 $G$ 类,它匹配的边的另一个端点归为 $B$ 类,继续搜索。
最后,就是最讨厌的一般图独有的情况:如果 $B$ 类点又遇到一个 $B$ 类点,这该怎么办呢?
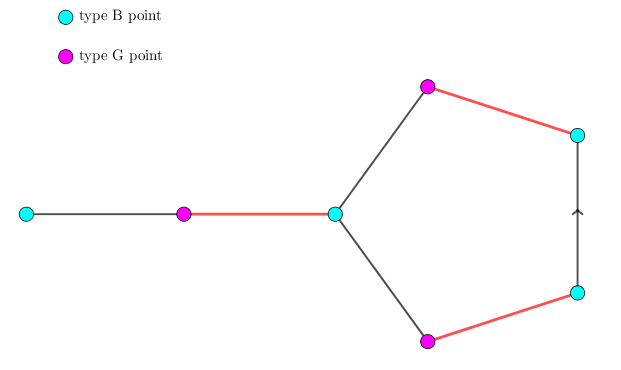
我们将这种情况的图画出来,可以发现,这其实是一个奇环 (长度为奇数的环):(图中青色点为 $B$ 类点,粉色点为 $G$ 类点,红色边为匹配边,灰色边为非匹配边,最左边的青色点为寻找增广路的端点 $v$)
这里我们要引入花的定义:
花:对于一个长度为 $2k + 1$ 的奇环 ($k \in \mathbb N^*$),如果其中有 $k$ 条匹配边,则称这个奇环为花 (blossom),其中 (在花中) 唯一的未匹配点称为花托 (base)。
有两个注意点:1. 对整张图而言,花托既可能是未匹配点,也可能是匹配点。2. 如果一个 $2k + 1$ 元环中匹配边的个数 $< k$,则这个奇环不是花。
对上图来说,这个 $5$ 元环中有 $2$ 条匹配边,则这个环就是一朵花,其中左边的青色点为花托。
可以证明,如果 $B$ 类点遇到 $B$ 类点,那么一定是遇到了一朵花,经过这两个 $B$ 类点。
对于这朵花,我们一定是最先枚举到了花托,然后在花中相遇。由于花中除了花托外的所有 $2k$ 个点都是匹配点,因此它们都不可能再与外面的点进行匹配。
对这朵花 (的 $2k$ 个节点) 中的任意一个节点 $u$,如果 $u$ 有一条连向花外的未匹配边。按照之前的算法,只有 $B$ 类点才能枚举未匹配边。但是!在花中,每个点都能向外枚举未匹配边,换句话说,花中的每个点都是 $B$ 类点!
如下图所示,花中的任意一个点向外连边,都是可以被增广到的 (只要选取合适的方向)!
因此,可以把整个花进行缩点操作,缩成一个 $B$ 类点,这个操作就叫缩花 (也叫开花?)。
注意在缩花的过程中,顺便维护一下每个点的 prev 数组 (可以发现连接 x 与 pre[x] 的边都是未匹配边)。
缩花后的 $B$ 点,可以看成是一个普通的点,可以与其它的点继续缩花。直到找到一条增广路,再将缩完的花展开即可。
因此结论 4 就是,当 $B$ 类点遇到 $B$ 类点,则形成一朵花,进行缩花操作,将花中的所有点改为 $B$ 类点,把花中每个点加入队列/栈进行增广。
有了这 4 个结论,我们就可以写出增广函数了。
关于如何求出花托的问题,其实花托就是搜索树中的 LCA 节点,可以 (通过 match 和 prev) 暴力跳 $B$ 类点来求,因为每次缩花至少缩掉 $2$ 个节点,缩花的次数不超过 $\dfrac V2$,具体的花可以用并查集的树形结构来维护 (其中并查集的祖先为花托)。
缩花是为找增广路服务的,因此找完一条增广路,找下一条时需要把原先的花清除掉。
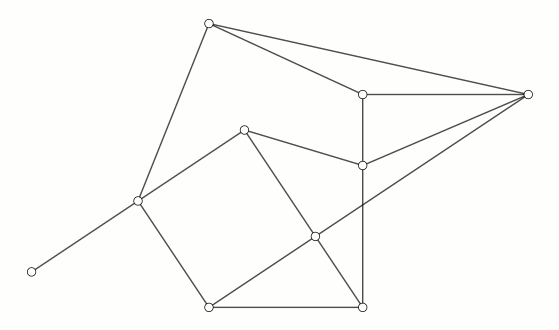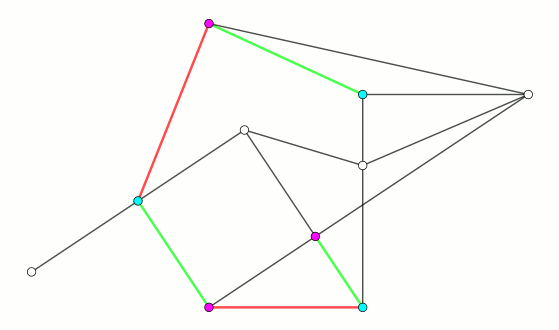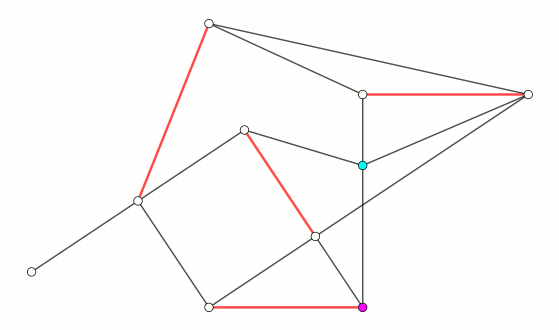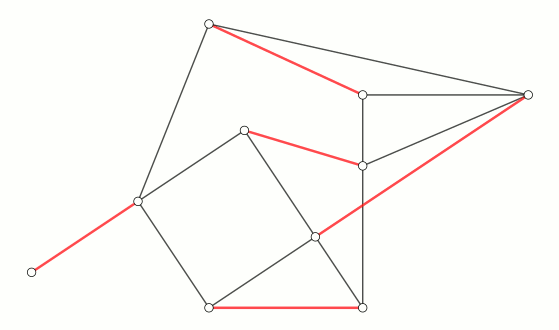
最后给个 demo GIF 来演示一下带花树算法运行的过程:
代码
坑
坑1:缩花的过程中,注意更新 prev 数组。
坑2:寻找 LCA (花托) 时,可以使用 hash 判断是否出现过。要注意当 $y = 0$ 时,就不要交换 $x, y$,否则花托可能会返回 $0$。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号