关于float 

 1 #include <iostream>
 2 using namespace std;
 3 
 4 void main()
 5 {
 6     float a = 1.0f;
 7     cout << (int)a << endl;
 8     cout << (int&)a << endl;
 9     cout << boolalpha << ((int)a == (int&)a) << endl;
10     float b = 0.0f;
11     cout << (int)b << endl;
12     cout << (int&)b << endl;
13     cout << boolalpha << ((int)b == (int&)b) << endl;
14 }
View Code

这个题非常好，考查浮点数在计算机中的表示。

现在一般的计算机浮点数都是使用IEEE754标准，可到如下网站恶补：

https://en.wikipedia.org/wiki/IEEE_754-1985

通过查看IEEE754标准可知，单精度浮点数的表示为：

1位表示符号位，8位表示指数位（需加127的指数偏移），23位表示尾数位

所以 0.1562510 = 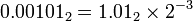0.00101_2 = 1.01_2 \times 2^{-3} 在计算机中的表示为

 

这样，上例中的浮点数 float a = 1.0f在计算机中的表示为

1.0 = 1.0x20

符号位    -> 0

指数部分 -> 0+127 = 01111111

尾数部分 -> 0

即 0011 1111 1000 0000 0000 0000 0000 0000 = 0x3f800000

所以

cout << (int)a << endl;

编译器的做法是取整数部分，即尾数部分1x2(127-127)=1

cout << (int&)a << endl;

编译器对引用的做法与强制类型转换又不一样，(int&)a相当于*(int*)&a，所以编译器并没有经过上述运算，直接将这个浮点数当作int类型来对待，故输出0x3f800000 = 1065353216。

所以其实引用与指针很相似，只不过不分配存储空间，且一经初始化就不可以再更改而已。它在传参时同样高效。

 

而float b = 0.0f是正0

在计算机中的表示为全0

即 0000 0000 0000 0000 0000 0000 0000 0000

所以cout << (int)b << endl; cout << (int&)b << endl;的结果都为0

=================================================================================================================

在论坛还看到一个例子，也很好

1 #include "stdio.h"
2 int main(void)
3 {
4     float a;
5     int b;
6     a=222222222;
7     b=(int)a;   
8     printf("%d",b);
9 }
View Code

问题为：

输出结果为什么会是222222224而不是222222222。

高手的解答很详细：

这个问题需要一步一步来解释：

我们先看看单精度浮点数的格式：
31 30...23 22...0，bit[31]表示符号位，bit[30...23]表示指数位，bit[22...0]表示尾数位。还有一个默认的整数部分为1。

1. float a = 222222222.
222222222 
=> 0b 1101 0011 1110 1101 0111 1000 1110 总共28个bit需去掉4位
=> 1.101 0011 1110 1101 0111 1000 1110 提取整数部分
=> 1.101 0011 1110 1101 0111 1001 [1110]去掉多余的部分且经过了round
开始组合
符号位：0
指数位：27+127（单精度偏置数）= 154= 0b 1001 1010
尾数位：0b 101 0011 1110 1101 0111 1001
最终结果：0b 0 1001 1010 101 0011 1110 1101 0111 1001
上面的结果就是a这个浮点数在内存中的二进制表示。

2. int b = (int)a.
0b 0 1001 1010 101 0011 1110 1101 0111 1001
=> 1.101 0011 1110 1101 0111 1001 乘以 2^27
=> 0b 1101 0011 1110 1101 0111 1001 0000 正数
=> 222222224

 =================================================================================================================

与上类似，double型的数也按上述规则转化，只不过数据长度稍有不同，如下：

以double 3.5为例：

3.510 = 11.12 = 1.112 x 2 1

=>

符号位    -> 0

指数部分 -> 1+1023 = 100 0000 0000

尾数部分 -> 11 -> 11 0000 ...

组合起来即为 0100 0000 0000 1100 ... = 0x400c0000 00000000

little endian的计算机表示为 00 00 00 00 00 00 0c 40

posted @ 2015-11-14 19:30  witxjp  阅读(337)  评论(0)  编辑  收藏  举报