**When your values are clear to you, making decisions become easier. **
— Roy E. Disney
一. 决策树模型
决策树算法属于监督学习,既可以解决回归问题,也可以解决分类问题。决策树由节点和有向边组成,如下图所示为决定是否去打网球的决策树,内部节点代表了特征属性,如“天空情况”;外部节点(叶子节点)代表了类别,如“Y”(去打网球),“N”(不去打网球):

决策树也可以看成一个if-then规则的集合,并且if-then规则集合有一个重要性质:互斥并且完备。也就是说,每一个实例都被一条路径或者一条规则所覆盖,并且只被一条路径或者一条规则所覆盖,例如上图中红线所示:
if ( 天空情况 == 晴 && 湿度 == 正常 ) then Y
决策树算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得对各个子数据集有一个最好的分类的过程,这一过程对应着对特征空间的划分,也对应着决策树的构建,如下图所示:
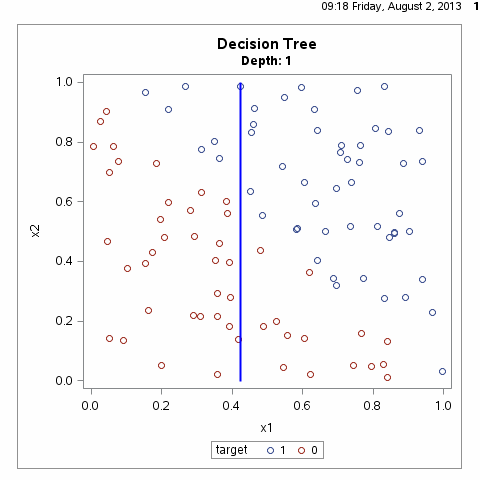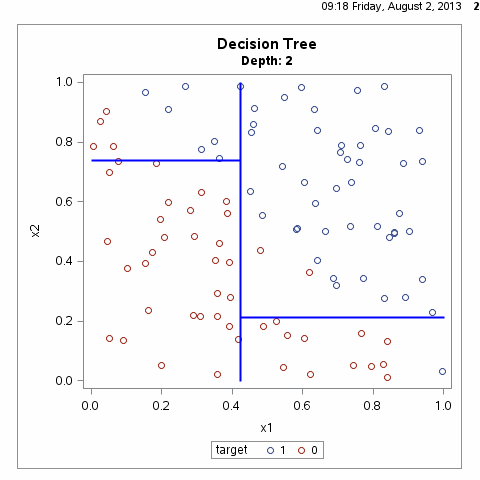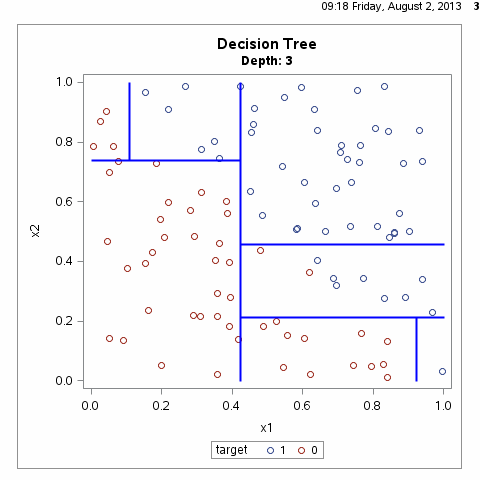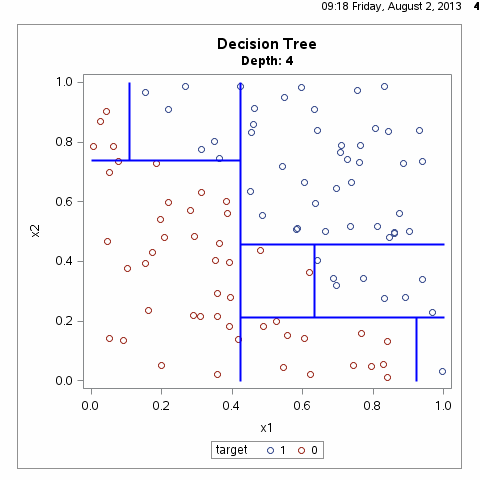
根据上图我们不难想到,满足样本划分的决策树有无数种,什么样的决策树才算是一颗好的决策树呢?
性能良好的决策树的选择标准是一个与训练数据矛盾较小的决策树,同时具有很好的泛化能力。也就是说,好的决策树不仅对训练样本有着很好的分类效果,对于测试集也有着较低的误差率。
二. 特征选择
上节提到决策树创建过程中会涉及特征空间划分,那么我们首先了解下特征划分的原则,假设有特征\(x\),类别\(y\):

如果在 \(x<3.5\) 处划分,我们得到最佳的划分;
如果在 \(x<4.5\) 处划分,就会出现分类错误。
核心思想:好的划分应该使样本变得纯粹(homogeneous)
有了特征划分的衡量标准,就可以选择能提供最好划分的特征,即进行特征选择。接下来我们来介绍衡量特征划分好坏的一些标准。
2.1 香农熵(shannon entropy)
1948 年,香农(Claude Elwood Shannon)提出了“信息熵”的概念,解决了对信息的量化度量问题。 一条信息的信息量大小和它的不确定性有直接的关系。比如说,我们要搞清楚一件非常非常不确定的事,或是我们一无所知的事情,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。
为了理解“信息熵”,我们先从bit说起,1 bit可以表示两个不同的结果,0或1(真或假)。假设1945年第二次世界大战中,电报员报告战争结果,如果纳粹投降,他会发送‘1’,如果纳粹不投降,他会发送‘0’。现在假设有四种可能的战争结果:
1)德国和日本都投降了;
2)德国投降,日本不投降;
3)日本投降,德国不投降;
4)两者都不投降。
电报员需要2 bit(00,01,10,11)来编码这条信息。同样,即使有256种不同的场景,电报员也只需要8 bit来编码。
假设纳粹投降的可能性为50%(\(p=1/2\))。然后,电报员报告他们投降了,我们消除总共2个事件(投降和不投降)的不确定性,这是\(p(=1/2)\)的倒数。因此如果事件发生是等可能的,已知一个事件刚刚发生时,就可以消除总共\(1/p\)个事件发生的可能性。例如,假设有4个事件,它们发生是等可能的(\(p=1/4\))。当一个事件发生时,意味着其他三个事件没有发生。因此,总共消除了4个事件的不确定性。
如果事件发生不是等可能的呢?假设纳粹有75%的可能投降,25%的可能不会投降。我们以黑点作为电报员的消息,如果已知纳粹没投降,那么4个点都可以抹去了,如下图所示:

如果已知纳粹投降了,那我们可以抹去多少个点呢?如下图所示:

我们可以抹去1个黑点 + 1/3个白点 = 1.333个点,即3/4的倒数,如下图所示:

香农认为任何事件的信息都可以用bit来衡量,为了将上面的不确定性换算成bit的数量,我们对抹去点的数量取对数(log) ,以2为底。
“投降”这一事件有多少信息?
$ log_2(1/0.75) = log_2(1.333) = 0.41$
“不投降”事件有多少信息?
$ log_2(1/0.25) = log_2 4 = 2 $
可以看出,不太可能发生的事件具有更高的熵。
每条消息所包含的信息量可以计算为:\(0.25 * log_24 + 0.75 * log_21.333= 0.81\)
我们再来重新算一下,假设纳粹投降的可能性为50%(\(p=1/2\)),也就是我们完全不确定,那么每条消息所包含的信息量可以计算为:\(0.5 * log_22 + 0.5 * log_22= 1\),信息熵更大。前面举了几个例子,接下来我们给出信息熵的正式定义:
设Y是一个取有限个值的离散随机变量,其概率分布为:
则随机变量Y的信息熵(或熵)定义为:
例:设随机变量Y为根据天气情况去打网球,则

2.2 条件熵(conditional entropy)
条件熵(conditional entropy)表示在随机变量X的条件下随机变量Y的不确定性度量。
设随机变量(X, Y),其联合概率分布为$ P(X, Y) = p_{ij}(i=1,2, ... , n; j=1,2, ... , m)\(,在随机变量X给定的条件下随机变量Y的条件熵\)H(Y|X)$,定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
这里,\(P(X=x_i)=p_i \qquad i=1,2, ... , n\)。设随机变量X为湿度,有两个取值:大,正常。则


2.3 信息增益(infomation gain)
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。 定义为:
2.2节的例子中湿度的信息增益为:
同上,计算天空情况,温度,风速的信息增益。每个特征的信息增益总结如下:
- 天空情况 = 0.247
- 温度 = 0.029
- 湿度 = 0.152
- 风速 = 0.048
因此将“天空情况”作为决策树的跟节点(root node),因为“天空情况”最有最大的信息增益。
按照上面的过程继续选择特征构建决策树:
“天空情况”是“晴”的样本集为:

分别对"温度"(Temperature),"湿度"(Humidity),"风速"(Windy)三个特征按照之前的方法进行选择,如下图,最终选择"湿度"(Humidity),它将子数据集彻底拆分了:

“天空情况”是“阴”的样本集为:

“天空情况”是“雨”的样本集为:

最终构建的决策树为:

这里需要注意的是并不是所有叶子节点都是相同类别;有时候类似的样本实例有不同的类别;拆分到不能继续拆分为止。
2.4 信息增益比(Information Gain Ratio)
信息增益比\(g_R(D, A)\)定义为其信息增益\(g(D, A)\)与训练数据集D关于特征A的值的熵\(H_A(D)\)之比,即
其中,\(H_A(D)=-\sum \limits_{i=1}^{n} \frac{|Di|}{|D|}*log2 \frac{|Di|}{|D|}\), n是特征A取值的个数。
2.5 基尼系数(Gini Index)
基尼系数\(Gini(D)\)表示集合\(D\)的不确定性,基尼系数越大,样本集合的不确定性也就越大,这一点与信息熵相似。对于给定的样本集合\(D\),其基尼系数为:
这里,\(C_k\)是\(D\)中属于第\(k\)类的样本子集。如果样本集合\(D\)根据特征\(A\)划分成n个部分,则在特征\(A\)的条件下,集合\(D\)的基尼指数定义为:
例如我们要拆分特征\(x\)和类别\(y\):

如果我们在\(x<3.5\)处拆分,\(Gini(D|A) = \frac{3}{8} \centerdot 0 + \frac{5}{8} \centerdot 0 = 0\);
而如果我们在\(x<4.5\)处拆分,\(Gini(D|A) = \frac{4}{8} \centerdot \frac{3}{8} + \frac{4}{8} \centerdot 0 = \frac{3}{16}\);
\(x\)在3.5处划分基尼系数更小,因此选择在3.5处划分。
三. ID3、C4.5及CART
不同的决策树学习算法选择特征的依据不同,但决策树的生成过程都是一样的(对特征进行贪婪的选择)。
ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征,每一次都选择使得信息增益最大的特征进行分裂,递归地构建决策树。但以信息增益作为划分训练数据集的特征的标准有一个致命的缺点,即选择取值比较多的特征往往会具有较大的信息增益,所以ID3偏向于选择取值较多的特征。
针对ID3算法的不足,C4.5算法根据信息增益比来选择特征,对这一问题进行了校正。
CART指的是分类回归树,它既可以用来分类,又可以被用来进行回归。CART用作回归树时用平方误差最小化作为选择特征的准则,用作分类树时采用基尼指数最小化原则,进行特征选择,递归地生成二叉树。
四. 树剪枝
剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段。在决策树学习中,为了尽可能正确分类训练样本,节点划分过程将不断重复,有时会造成决策树分支过多,这时就有可能因训练样本学的“太好了”,以至于把训练集自身的一些特点当作所有数据都具有的性质而导致过拟合。
决策树剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(postpruning)两种:
- 预剪枝是在决策树生成过程中,对树进行剪枝,提前结束树的分支生长;
- 后剪枝是在决策树生长完成之后,对树进行剪枝,得到简化版的决策树。
不论是预剪枝还是后剪枝,都需要先确定判断是否剪枝的标准,即根据什么决定是否剪枝呢?周志华的西瓜书中介绍的是评估泛化性能:假设采用留出法,即将数据集(数据集见西瓜书中表4.2)划分为训练集和验证集,如果采用预剪枝策略,则对每个节点在划分前先进行评估,若当前节点的划分不能带来决策树泛化性能提升,则停止划分并将当前节点标记为叶节点,比如下图中的节点①,如果不划分,验证集精确度为42.9%,如果划分验证集精确度提高到71.4%,因此预剪枝决策是划分,而节点②根据特征选择标准选择“色泽”来进行划分,划分前验证集的精度是71.4%,而划分后降低到57.1%,因此因此预剪枝决策是不划分,节点③同理。预剪枝基于“贪心”思想,尽量不让分支展开,可能给决策树带来欠拟合的风险:

如果采用后剪枝策略,先生成完整决策树,再自底向上对每一个非叶子进行考察,若将该节点对应的子树替换为叶节点(一般选择多数来作为新的叶节点类别)能带来泛化性能的提升,则将该子树替换为叶节点,例如下图是剪枝后的决策树,红色箭头指向剪枝后新生成的叶节点,西瓜书中提还提到后剪枝通常比预剪枝决策树保留了更多的分支,降低了欠拟合的风险:




