20200924-5 四则运算试题生成,结对
此作业的要求参见:https://edu.cnblogs.com/campus/nenu/2020Fall/homework/11245
结对对象:侯文鑫同学
一.代码说明:选择语言为python; 开发环境为PyCharm; python版本为:3.8.6
对作业要求的功能一、二、三进行合并编程
功能1. 四则运算
支持出题4个数的四则运算题目,所有题目要求作者有能力正确回答 (提示:1/3 != 0.33333333333333333333333333333333,而是无限长)。
功能2. 支持括号
老师看了你的表演,大大赞赏了你。然后她说,"你的题库里怎么都是没有括号的题呢,我记得你当初括号就掌握得不好啊。"你的脸红了,对老师说,"给我2个小时时间,我给你一个新版本,有括号的。"
你拿出笔记本,偷偷微信你们《构建之法》班的学霸,她说肯定能行,但是细节信号不好你听不清,只捕捉到隐约几个词"逆波兰""后缀表达式""堆栈""我看好你""数据结构"。
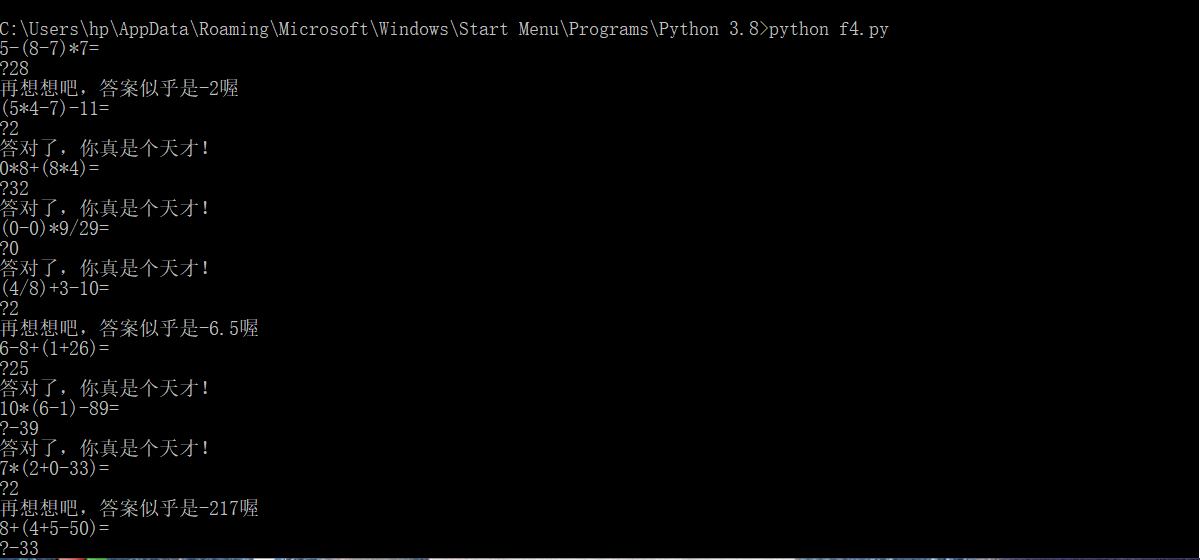
功能一、二运行截图:

功能3. 限定题目数量,"精美"打印输出,避免重复
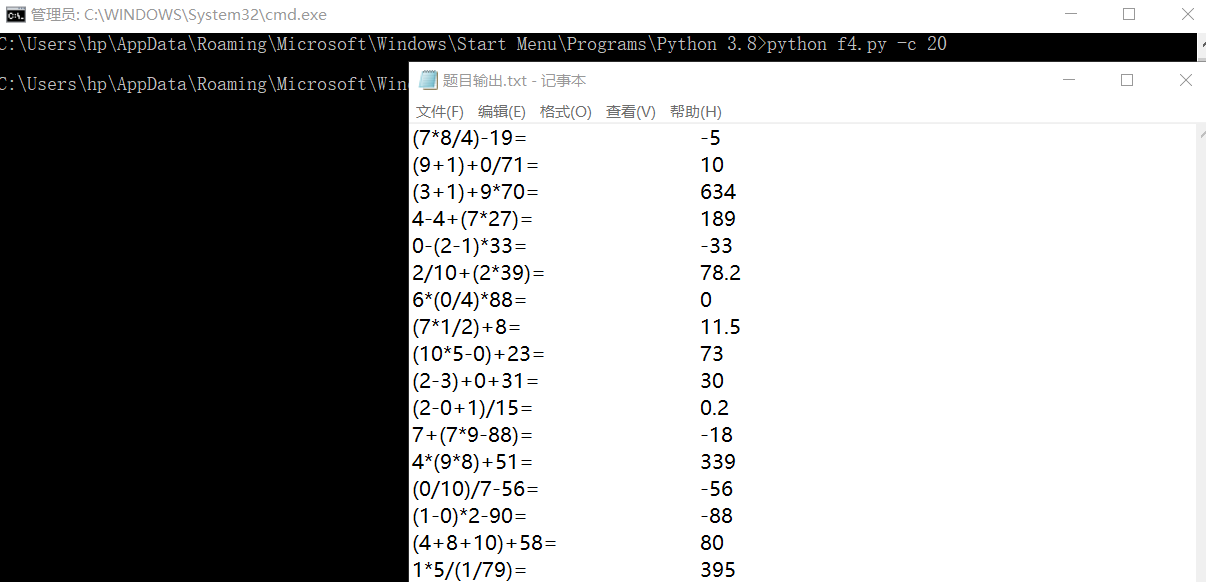
功能三运行截图:
功能4. 支持分数出题和运算

二.代码分析、重难点分析
对于功能一的算法实现,首先要考虑利用随机函数生成四个整型数和三个操作符,此处调用random()函数进行实现。对于算式的运算还要考虑到四则运算的优先级,先乘除后加减。
对于功能二的括号,参考了往届学长的代码,我们列举了四个数字和三个操作符在存在括号的情况下的所有可能性。在每种情况下匹配追加其右括号。
下面是生成算式和确定括号位置的代码:
def create_formula(): # 随机生成算式
equation = []
for i in range(3): # 随机生成前三个数字和操作符
equation.append(random.randint(0, 10)) # 随机生成0到100的整数型随机数
equation.append(operator[random.randint(0, 3)]) # 为随机生成操作符生成0到3的整数型随机数
equation.append(random.randint(0, 100)) # 随机在0到100内生成第四个数字
p = random.randint(1, 5) # 括号存在的位置
if p == 1: # 括号括前两位数字
equation.insert(0, "(")
equation.insert(4, ")")
elif p == 2: # 括号括前三位数字
equation.insert(0, "(")
equation.insert(6, ")")
elif p == 3: # 括号括二三位数字
equation.insert(2, "(")
equation.insert(6, ")")
elif p == 4: # 括号括后三位数字
equation.insert(2, "(")
equation.append(")")
elif p == 5: # 括号括后两位数字
equation.insert(4, "(")
equation.append(")")
return equation
在思考转化逆波兰式的过程,我们讨论和查找了数据结构中栈的内容和栈的初始化定义,以及出栈入栈的操作。
在随机生成算式后,再通过逆波兰式,也就是后缀表达式存入定义的栈中。下面是转化逆波兰式的代码:
def inverse_polish(formula): # 转化逆波兰表达式
result = []
c = []
slist = [i for i in formula]
for item in slist:
if item in range(0, 100):
result.append(item)
elif not c and item in operator1.keys():
c.append(item)
continue
elif c and item in operator1.keys():
for x in range(c.__len__()):
z = c[-1]
temp = operator1[z] if z in operator1 else brackets[z]
if temp >= operator1[item]:
result.append(c.pop())
else:
c.append(item)
break
if not c:
c.append(item)
elif item == ")":
for x in range(c.__len__()):
if c[-1] == "(":
c.pop()
break
else:
result.append(c.pop())
elif item == "(":
c.append(item)
for x in range(c.__len__()):
result.append(c.pop())
return result
对于结果也是依赖栈进行计算的
def calculate(re_formula):
stack = Stack()
sum = 0
if len(re_formula) == 0:
return sum
for i in re_formula:
if i in range(0, 100):
stack.push(float(i))
elif '+' == i:
a = stack.pop() # a 后进栈
b = stack.pop()
stack.push(b + a)
elif '-' == i:
a = stack.pop()
b = stack.pop()
stack.push(b - a)
elif '*' == i:
a = stack.pop()
b = stack.pop()
stack.push(b * a)
elif '/' == i:
a = stack.pop()
b = stack.pop()
if a == 0:
return False
else:
stack.push(b / a)
return stack.pop()
而对于我们使用的列表的输出和追加也是我们两个人讨论的最多的一个部分,下面是功能一的实现代码:
def function_one():
correct = 0
i = 0
while i in range(20):
i = i + 1
formula = create_formula() # 生成表达式
re_formula = inverse_polish(formula)
result = calculate(re_formula)
answer0 = result # 表达式计算的值
if result is False or len(str(result)) > 15:
i = i - 1
continue
str_formula = "".join("%s" % id for id in formula)
print(str_formula + "=")
print("?", end="") # end在输出中自动包含换行的默认行为
answer = float(input())
if abs(result - int(result)) < 1.0e-16:
result = int(result)
if answer == answer0:
print("答对了,你真是个天才!")
correct += 1
else:
print("再想想吧,答案似乎是" + repr(result) + "喔") # repr函数将对象转化为解释器可读的形式
print("你一共答对" + repr(correct) + "道题,共%d道题" % i)
功能三的难点在于将算式和结果写入文件并对齐格式,这里对于文件的读入和格式控制也是思考了非常久的一个难点:
def function_one():
correct = 0
i = 0
while i in range(20):
i = i + 1
formula = create_formula() # 生成表达式
re_formula = inverse_polish(formula)
result = calculate(re_formula)
answer0 = result # 表达式计算的值
if result is False or len(str(result)) > 15:
i = i - 1
continue
str_formula = "".join("%s" % id for id in formula)
print(str_formula + "=")
print("?", end="") # end在输出中自动包含换行的默认行为
answer = float(input())
if abs(result - int(result)) < 1.0e-16:
result = int(result)
if answer == answer0:
print("答对了,你真是个天才!")
correct += 1
else:
print("再想想吧,答案似乎是" + repr(result) + "喔") # repr函数将对象转化为解释器可读的形式
print("你一共答对" + repr(correct) + "道题,共%d道题" % i)
而对于功能四分数运算的实现,我们依然考虑操作符的优先级和对栈的依赖。这个功能的代码实现不依赖逆波兰式。对于算式中数字和运算符的随机产生也依然是放入列表中。
priority = {"+": 1, "-": 1, "*": 2, "/": 2} # 对优先级的定义
while i < n:
i = i + 1
first_num = random.randint(1, 10)
second_num = random.randint(1, 10)
third_num = random.randint(1, 10)
fourth_num = random.randint(1, 10)
if second_num == 1:
x = first_num
else:
x = fractions.Fraction(first_num, second_num) # 第一个数是分子、第二个是分母
if fourth_num == 1:
y = second_num
else:
assert isinstance(fourth_num, object)
y = fractions.Fraction(second_num, fourth_num)
fifth_num = random.randint(1, 10)
sixth_num = random.randint(1, 10)
a = random.choice("+-*/")
b = random.choice("+-*/")
c = random.choice("+-*/")
list0 = [x, a, y, b, fifth_num, c, sixth_num]
equation = " ".join('%s' % id for id in list0)
stack = PyStack()
stack.push(x)
stack.push(y)
if priority[b] > priority[a]: # 先算第二个第三个数
stack.push(operate(stack.pop(), fifth_num, b))
if priority[c] > priority[a]: # 再算四个数字
stack.push(operate(stack.pop(), sixth_num, c))
stack.push(operate(stack.pop(), stack.pop(), a))
else: # 再算第一个数字
stack.push(operate(stack.pop(), stack.pop(), a))
# 再算最后一个
stack.push(operate(stack.pop(), sixth_num, c))
else: # 先算第一个第二个
stack.push(operate(stack.pop(), stack.pop(), a))
if priority[c] > priority[b]: # 再算第三第四个
if len(str(operate(fifth_num, sixth_num, c))) > 15:
i = i-1
continue
stack.push(operate(fifth_num, sixth_num, c))
stack.push(operate(stack.pop(), stack.pop(), b))
else:
stack.push(operate(stack.pop(), fifth_num, b))
stack.push(operate(stack.pop(), sixth_num, c))
print('%-30s %-30s' % (equation+'=', stack.pop()))
三.结对编程体会(在编码、争论、复审等活动中花费时间较长,给你较大收获的事件)
(1)首先在对语言的选择上,我们最初考虑了C,因为对C的熟悉程度更高,但是在一起认真的的分析了题目的功能要求后,觉得C的代码实现起来会过于的复杂和困难,于是我们统一决定了将编程语言改为python,虽然两个人也都是刚刚接触但还是决定一起探索尝试。
(2)编码的过程中,对于随机产生运算数和运算符以及对于考虑优先级的过程的思路和想法都是统一的,但是随机产生的元素我们都是存进列表中,而对于如何将列表中的元素连接起来形成完整正常的算式这一过程,我们真的争论了非常久。因为双方对列表追加的理解有出入,虽然我们都知道生成后的元素都是按顺序存在于列表中了,但是最初我们没有考虑到,元素其实就是只是存在而并未连接在一起,和字符串不同的是不能直接通过"+"就连在一起。通过查找了很多相关的函数,我们认真的讨论了append()追加函数的使用方法和思路。误区是我们只追加进列表但并未连接算式。真正对于算式的形成并不是在我们将随机元素后产生后,而是要另外调用.join()函数。
(3)功能二中括号的位置我们第一反应都是随机放置,但是随机放置又要考虑左右括号不能重复和顺序的问题,我们最后用了最原始的办法,也是考虑到就算我们列举出所有的可能性也不算很多,所以直接在纸上列出所有括号存在的可能,然后将每一种可能性都写进代码中实现。
(4)对于栈和逆波兰式的学习也是我们花费很长时间的一个部分。但是除了在功能三中使用了栈,我们在功能四的中栈的构建也是复制功能三中一样的思路,这一点收获非常大。而写入文件和对于输出在文本文件中的格式问题,也是我们修改了很多次的地方。
(5)贯穿整个结对编程的一个问题就是两个人都因为python的缩进吃了很多苦头,由于python对于缩进的敏感和两人接触的都不是很成熟,出现过很多次马虎的失误,但也都在审查中相互提醒改正了。代码风格其实也很不同,我的习惯是怕自己忘记如果有过多的变量名或是函数定义非常喜欢加注释提醒自己,这一点上其实也为后来我们检查代码提供了方便。
四.结对编程的证明照片

五.使用coding.net做版本控制。
https://e.coding.net/mochi0828/f4/formula.git



