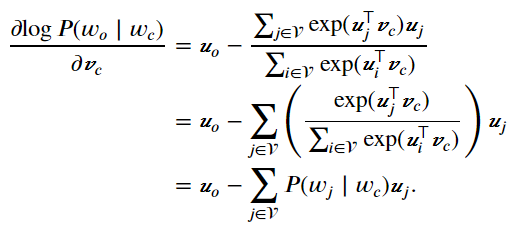Word2vec

一、Word2vec简介

  一个将词表示为含有语义信息的向量的模型。
  一段文本——> 向量表示——>含有语义信息的向量表示。
例如：
输入:自然 语言 处理 包含 很多

二、CBoW

CBoW原理图

  通过上下文预测中间词。设置窗口为2，根据同中心词距离不超过2的背景词，生成中心词。即根据“自然”、“语言”、“包含”、“很多”预测生成“处理”的概率。
  因为连续词袋模型的背景词有多个，我们将这些背景词向量取平均，然后使用和Skip-gram模型一样的方法来计算条件概率。设\(v_{i}\)和\(u_{i}\)分别表示词典中索引为i的词作为背景词和中心词的向量（注意符号的含义与跳字模型中的相反）。设中心词w_{c}在词典中索引为c，背景词\(w_{o_{1}},...,w_{o_{2m}}\)在词典中索引为o_{1},...,o_{2m}，那么给定背景词生成中心词的条件概率:

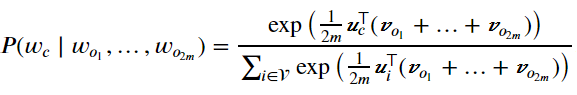
令\(W_{o}=\left \{ w_{o_{1}},...,w_{o_{2m}} \right \}\)，\(\hat{v}_{o}=\left ( v_{o_{1}}+...+v_{o_{2m}} \right )/\left ( 2m \right )\)，化简后的公式如下：

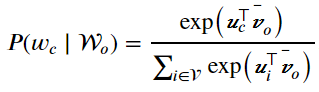
  给定一个长度为T的文本序列，设时间步t的词为\(w^{\left ( t \right )}\)，背景窗口大小为m。连续词袋模型的似然函数是由背景词生成任一中心词的概率。

  损失函数定义为log函数处理最大似然估计后的反函数。


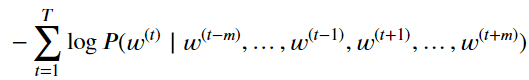
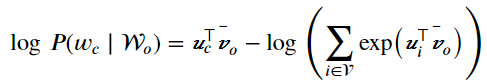
  可以计算出上式中条件概率的对数有关任一背景词向量\(v_{o_{i}}\)\(\left ( i=1,...,2m \right )\)的梯度

三、Skip-gram

Skip-gram原理图

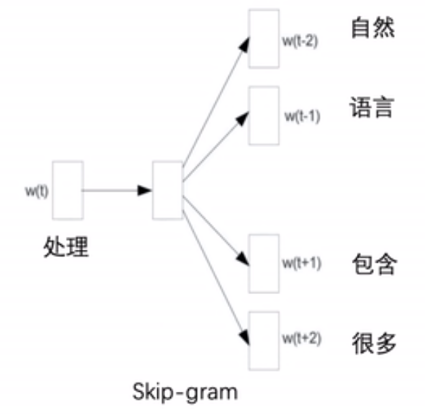
  通过中心词预测上下文。设置窗口为2，生成与中心词距离不超过2的背景词的条件概率。即根据“处理”预测生成“自然”、“语言”、“包含”、“很多”的概率。
\(P\left ( "自然","语言","包含","很多"\mid "处理" \right )\)
假设给定中心词的情况下，背景词的生成是相互独立的，那么上式可以改写成
\(P\left ( "自然"\mid "处理" \right )\cdot P\left ( "语言"\mid "处理" \right )\cdot P\left ( "包含"\mid "处理" \right )\cdot P\left ( "很多"\mid "处理" \right )\)
  在Skip-gram模型中，每个词被表示成两个d维向量，用来计算条件概率。假设这个词在词典中索引为i，当它为中心词时向量表示为\(v_{i}\)，而为背景词时向量表示为\(u_{i}\)。设中心词\(w_{c}\)在词典中索引为c，背景词\(w_{o}\)在词典中索引为o，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

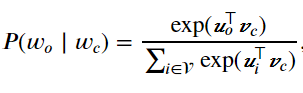
  其中词典索引集\(v=\left \{ 0,1,...,\left | v \right |-1\right \}\)。假设给定一个长度为T的文本序列，设时间步t的词为\(w^{\left ( t \right )}\)。假设给定中心词的情况下背景词的生成相互独立，当背景窗口大小为m时，跳字模型的似然函数即给定任一中心词生成所有背景词的概率。

  损失函数定义为log函数处理最大似然估计后的反函数。


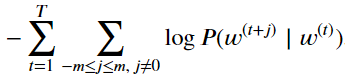
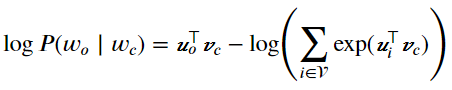
  参数梯度的求导。