RNN-2-前向传播、BPTT反向传播

一、RNN的网络结构

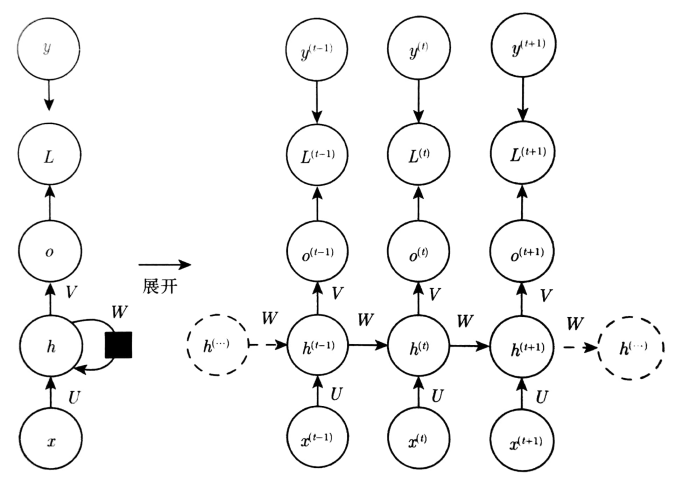
二、前向传播

  假定隐藏单元的激活函数是tanh，输出是离散的。表示离散变量的常规方式是把输出O作为每个离散变量可能值的非标准化对数概率。然后经softmax函数处理后，获得标准化后概率的输出向量\(\hat{y}\)。RNN从特定的初始状态\(h^{\left ( 0 \right )}\)开始传播。从t=1到\(t=\tau\)的每个时间步，更新方程如下：

  其中b和c是偏置向量权重矩阵U、V、W分别对应输入到隐层，隐层到输出，隐层到隐层的连接。这个神经网络将一个输入序列映射到相同长度的输出序列。与x序列配对的y的总损失为所有时间步的损失之和。
例如：\(L^{\left ( t \right )}\)为给定的\(x^{\left ( 1 \right )},...,x^{\left ( t \right )}\)后\(y^{\left ( t \right )}\)的负对数似然（最大似然估计的反数，可用作损失函数，进一步通过梯度下降来确定各参数值）。

  其中\(p_{model}\left ( y^{\left ( t \right )}\mid \left \{ x^{\left ( 1 \right )},...,x^{\left ( t \right )} \right \} \right )\)需要读取模型输出的向量
\(\hat{y}^{\left ( t \right )}\)中对应于\(y^{\left ( t \right )}\)的项。

三、BPTT（back-propagation through time）反向传播

  使用BPTT计算RNN的公式中用红色框线框出来的公式。包括参数U、V、W、b、c以及以t为索引的节点序列\(x^{\left ( t \right )}\)、\(h^{\left ( t \right )}\)、\(o^{\left ( t \right )}\)、\(L^{\left ( t \right )}\)。对于每一个节点N，我们需要基于N后面的节点的梯度，递归的计算梯度\(\bigtriangledown_{N}L\)。从离最终损失最近的节点开始递归：

  在这个导数中，假设输出\(o^{\left ( t \right )}\)作为softmax函数的参数，从softmax可以获得关于输出的概率向量\(\hat{y}\)，所有i、t，关于时间步t输出的梯度\(\bigtriangledown_{o^{\left ( t \right )}}L\)如下：

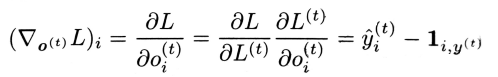
对化简公式的过程进行补充：

  从序列的尾端开始，反向计算。在最后的时间步$\tau \(，\)h^{\left ( \tau \right )}\(只有\)o^{\left ( \tau \right )}$作为后续节点，因此该梯度很简单。

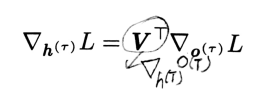
  从时刻\(t=\tau -1\)到t=1反向迭代，通过时间反向传播梯度，注意\(h^{\left ( t \right )}\left ( t<\tau \right )\)同时具有\(o^{\left ( t \right )}\)和\(h^{\left ( t+1\right )}\)两个后续节点。因此，它的梯度由下式计算:

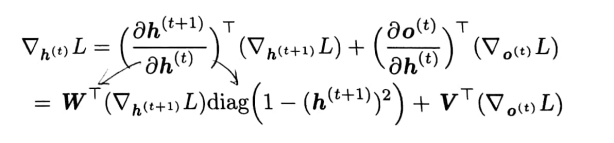
对化简公示的补充：

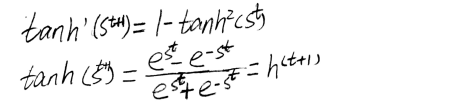
  其中\(diag(1-\left ( h^{t+1} \right )^{2})\)表示包含元素\(1-\left ( h^{t+1} \right )^{2}\)的对角阵。这是关于时刻t+1与隐藏单元i关联的双曲正切的Jacobian。
  定义只在t时刻使用虚拟变量\(W^{\left ( t \right )}\)作为W的副本。然后使用\(\bigtriangledown_{W^{\left ( t \right )}}\)表示权重在时间步t对梯度的贡献。剩下参数的梯度如下：

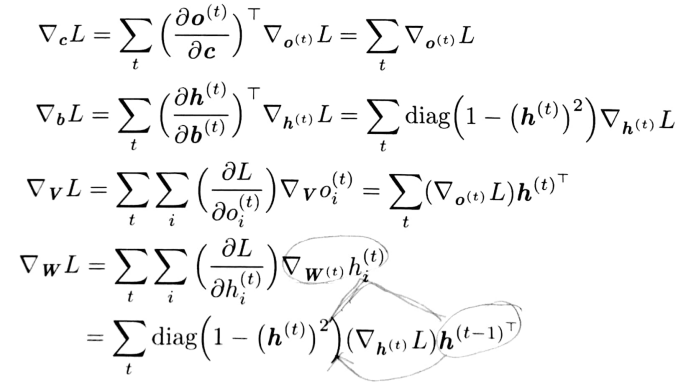
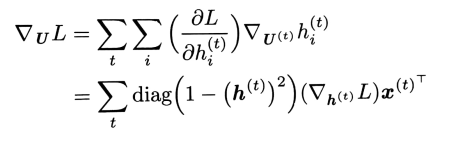
三、总结

  理论上循环神经网络可以支持任意长度的序列，然而在实际训练过程中，如果序列过长，一方面会导致优化时出现梯度消散和梯度爆炸的问题，另一方面，展开后的前馈神经网络会占用过大的内存，所以实际中会规定一个最大长度，当序列长度超过规定长度之后会对序列进行截断。