线性回归

一、线性回归

  定位：监督学习，回归用于预测输入变量和输出变量之间的关系。
  回归问题的学习等价于函数拟合：使用一条函数曲线使其很好的拟合已知函数且很好的预测未知数据。

二、回归问题分类

  回归问题按照输入变量的个数可以分为一元回归和多元回归；按照输入变量和输出变量之间关系的类型，可以分为线性回归和非线性回归。

1、一元线性回归

公式：y = ax + b

误差公式：

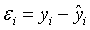(1)

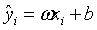
误差服从高斯分布：

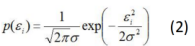
(1)式代入(2)式：

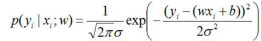
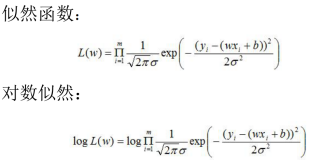
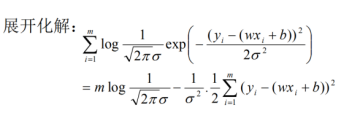
  对数似然函数越大预测结果越好，此时目标函数即预测值与真实值之间的误差就越小。

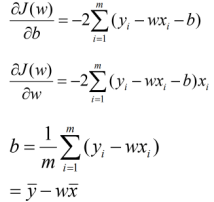
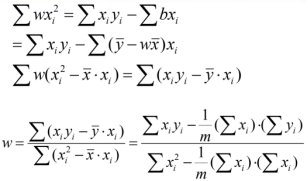
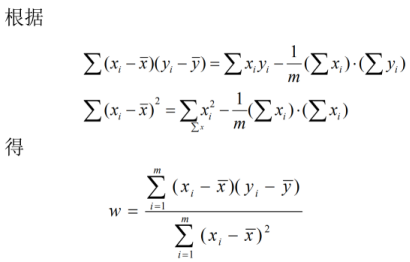
2、多元线性回归

  多元线性回归：有两个或两个以上的自变量，就称为多元回归。

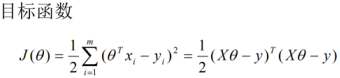
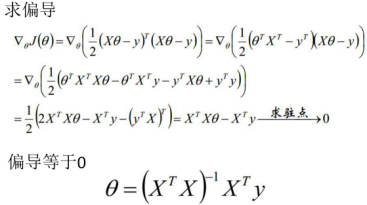
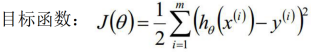
3、优化目标函数采用梯度下降算法

步骤：

1、初始化参数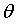

2、梯度更新公式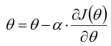
其中α表示学习率在线性回归中，目标函数收敛而且为凸函数，是有一个极值点，所以局部最小值就是全局最小值。