常见的深度学习优化器
优化器的使用:在机器学习与深度学习中,主要应用于梯度下降。比如:传统的优化器主要结合数据集,通过变化单次循环所采用的数据量的大小来对梯度下降进行控制;非传统的优化器则进一步结合数据集的特点和模型的训练时间,以不同的形式变化梯度下降的学习率。常见的优化器SGD、BGD、MBGD、Momentum、NAG、Adagrad、RMSprop、Adam梯度下降的原理:$\theta ^{n+1}=\theta ^{n}-\eta \bigtriangledown _{\theta }J\left ( \theta \right )$其中$\eta$为学习率;$\theta ^{n}$为更新前的参数;$\theta ^{n+1}$为更新后的参数;$ \bigtriangledown _{\theta }J\left ( \theta \right )$是当前参数的导数。 1.SGD(Stochastic Gradient Descent )SGD随机梯度下降参数更新原则:单条数据就可对参数进行一次更新。优点:参数更新速度快。 缺点:由于每次参数更新时采用的数据量很小,造成梯度更新时震荡幅度大,但大多数情况都是向着梯度减小的方向。 
2.BGD(Batch Gradient Descent )BGD批量梯度下降参数更新原则:所有数据都参与参数的每一次更新。优点:由于每次参数更新时采用的数据量很大,梯度更新时很平滑。 缺点:由于每次参数更新时采用的数据量很大,造成参数更新速度慢。 
3.MBGD(Mini-Batch Gradient Descent )MBGD小批量梯度下降参数更新原则:只用所有数据的一部分进行参数的每一次更新。优点:相比于SGD,由于每次参数更新时采用的数据量相对较大,梯度更新时相对平滑;相比于BGD,由于每次参数更新时采用的数据量相对较小,参数更新速度相对较快。 缺点:没有考虑数据集的稀疏度和模型的训练时间对参数更新的影响。 
4.MomentumMomentum解决的问题:SGD随机梯度下降时的震荡问题。Momentum参数更新原则:通过加入 $\gamma v_{n}$ ,加速 SGD, 并且抑制震荡。 更新公式: $v_{n+1}=\gamma v_{n}+\eta \bigtriangledown _{\theta }J\left ( \theta \right )$ $\theta ^{n+1}=\theta ^{n}-v_{n+1}$ 超参数设定值: 一般$\gamma$取值 0.9 左右。 优点:加入的这一项,可以使得梯度方向不变的维度上速度变快,梯度方向有所改变的维度上的更新速度变慢,这样就可以加快收敛并减小震荡。 缺点:这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚,如果它能具备一些先知,例如快要到坡底时,就知道需要减速了的话,适应性会更好。 5.NAG(Nesterov Accelerated Gradient)NAG解决的问题:在Momentum的基础上进一步解决SGD随机梯度下降时的震荡问题。NAG参数更新原则:用 $\theta -\gamma v_{n}$ 来近似当做参数下一步会变成的值,则在计算梯度时,不是在当前位置,而是未来的位置上。 更新公式: $v_{n+1}=\gamma v_{n}+\eta \bigtriangledown _{\theta }J\left ( \theta- \gamma v_{n} \right )$ $\theta ^{n+1}=\theta ^{n}-v_{n+1}$ 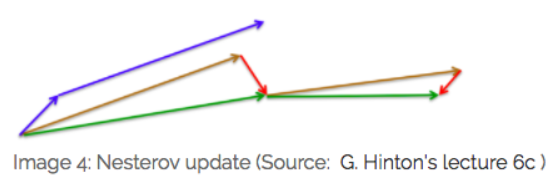 超参数设定值: 一般$\gamma$仍取值 0.9 左右。 优点:蓝色是 Momentum 的过程,会先计算当前的梯度,然后在更新后的累积梯度后会有一个大的跳跃。而NAG 会先在前一步的累积梯度上(brown vector)有一个大的跳跃,然后衡量一下梯度做一下修正(red vector),这种预期的更新可以避免我们走的太快。 应用:NAG 可以使 RNN 在很多任务上有更好的表现。 缺点:不能根据参数的重要性而对不同的参数进行不同程度的更新。 6.Adagrad(Adaptive gradient algorithm)Adagrad解决的问题:解决不能根据参数的重要性而对不同的参数进行不同程度的更新的问题。Adagrad参数更新原则:对低频的参数做较大的更新,对高频的做较小的更新。 更新公式: $\theta _{t+1,i}=\theta _{t,i}-\frac{\eta }{\sqrt{G_{t,ii}+\epsilon }}g_{t,i}$ 其中$g$为$t$时刻$\theta _{i}$的梯度。 $g_{t,i}=\bigtriangledown _{\theta }J\left ( \theta _{i} \right )$ 如果是普通的 SGD, 那么$\theta _{i}$在每一时刻的梯度更新公式为: $\theta _{t+1,i}=\theta _{t,i}-\eta g_{t,i}$ 其中 $G_{t,ii}$是个对角矩阵, $(i,i)$ 元素就是$t$ 时刻参数 $\theta _{i} $ 的梯度平方和。 超参数设定值:一般$ \eta$ 选取0.01。 优点:减少了学习率的手动调节。 缺点:它的缺点是分母会不断积累,这样学习率就会收缩并最终会变得非常小。 7.AdadeltaAdadelta解决的问题:解决Adagrad分母会不断积累,这样学习率就会收缩并最终会变得非常小的问题。Adadelta参数更新原则:和 Adagrad 相比,就是分母的 $G_{t,ii}$ 换成了过去的梯度平方的衰减平均值,指数衰减平均值。 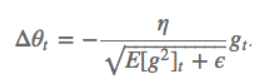 这个分母相当于梯度的均方根 root mean squared (RMS),在数据统计分析中,将所有值平方求和,求其均值,再开平方,就得到均方根值 ,所以可以用 RMS 简写: 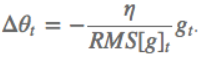 其中 $E$ 的计算公式如下,$t$ 时刻的依赖于前一时刻的平均和当前的梯度: 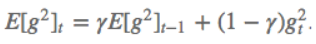 更新公式: 此外,还将学习率$ \eta$换成了 $RMSE\left ( \bigtriangleup \theta \right )$,这样的话,我们甚至都不需要提前设定学习率了: 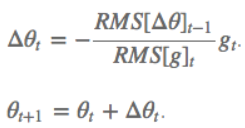 超参数设定值: $\gamma$一般设定为 0.9。 优点:减少了学习率的手动调节。 8.RMSpropRMSprop解决的问题:RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题。RMSprop参数更新原则:RMSprop 与 Adadelta 的第一种形式相同:(使用的是指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动。允许使用一个更大的学习率$ \eta$)。 更新公式: 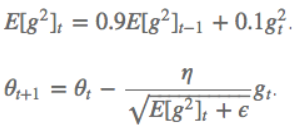 超参数设定值:Hinton 建议设定 $\gamma$为 0.9, 学习率$ \eta$ 为 0.001。 优点:减少了学习率的手动调节。 9.Adam(Adaptive Moment Estimation)Adam解决的问题:这个算法是另一种计算每个参数的自适应学习率的方法。Adam参数更新原则:相当于 RMSprop + Momentum。除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方$ v_{t}$ 的指数衰减平均值 ,也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值:   更新公式: 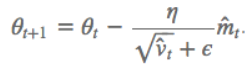 超参数设定值:建议 β1 = 0.9,β2 = 0.999,ϵ = 10e−8。 优点:实践表明,Adam 比其他适应性学习方法效果要好。 如何选择优化算法?1.如果数据是稀疏的,就用自适用方法,即 Adagrad, Adadelta, RMSprop, Adam。2.RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum,随着梯度变的稀疏,Adam 比 RMSprop 效果会好。 3.整体来讲,Adam 是最好的选择 4.SGD 虽然能达到极小值,但是比其它算法用的时间长,而且可能会被困在鞍点。 5.如果需要更快的收敛,或者是训练更深更复杂的神经网络,需要用一种自适应的算法。 |



