矩阵求导

矩阵的迹求导法则

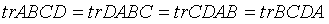
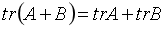
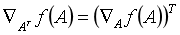
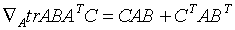
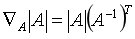
矩阵的求导计算法则

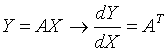
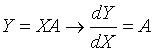
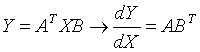
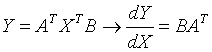
乘积的导数

一些结论：

1.矩阵\(Y\)对标量\(X\)求导：
相当于每个元素求导数后转置一下，注意\(m\times n\)矩阵求导后变成了\(n\times m\)

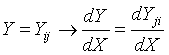
2.标量\(y\)对列向量\(X\)求导：
注意与上面不同，这次括号内是求偏导，不转置，对\(n\times 1\)向量求导后还是\(n\times 1\)向量

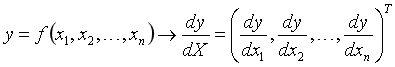
3.行向量\(Y^{T}\)对列向量\(X\)求导：
注意\(1\times m\)向量对\(n\times 1\)向量求导后是\(n\times m\)矩阵。
将的\(Y\)每一列对\(X\)求偏导，将各列构成一个矩阵。
重要结论：


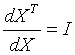
4.列向量\(Y\)对行向量\(X^{T}\)求导：
转化为行向量\(Y^{T}\)对列向量\(X\)的导数，然后转置。
注意\(m\times 1\)向量对\(1\times n\)向量求导结果为\(m\times n\)矩阵。

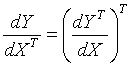
5.向量积对列向量\(X\)求导运算法则：
注意与标量求导有点不同。


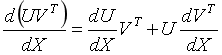
重要结论：



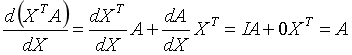
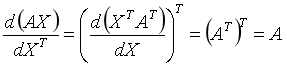
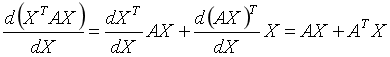
6.矩阵\(Y\)对列向量\(X\)求导：
将\(Y\)对\(X\)的每一个分量求偏导，构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
7.矩阵积对列向量求导法则：


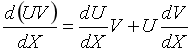
重要结论：

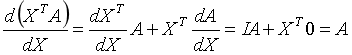
8.标量\(y\)对矩阵\(X\)的导数：
类似标量\(y\)对列向量\(X\)的导数，
把\(y\)对每个\(X\)的元素求偏导，不用转置。

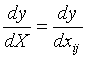
重要结论：
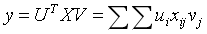于是
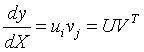
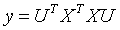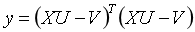则
则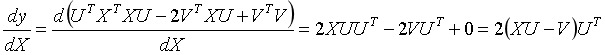
9.矩阵\(Y\)对矩阵\(X\)的导数：
将\(Y\)的每个元素对\(X\)求导，然后排在一起形成超级矩阵。
10.乘积的导数

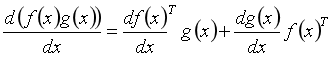
结论