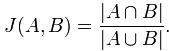Approximate Nearest Neighbors.接近最近邻搜索
有少量修改;如有疑问,请看链接原文.....
1.Survey:
Nearest neighbor search (NNS), also known as proximity search,similarity search orclosest point search, is anoptimization problem for finding closest (or most similar) points. Closeness is typically expressed in terms of a dissimilarity function: The less similar are the objects the larger are the function values. Formally, the nearest-neighbor (NN) search problem is defined as follows: given a setS of points in a spaceM and a query pointq ∈ M, find the closest point inS toq. Donald Knuth in vol. 3 of The Art of Computer Programming (1973) called it thepost-office problem, referring to an application of assigning to a residence the nearest post office. A direct generalization of this problem is ak-NN search, where we need to find thek closest points.寻找高维近邻点的最优化问题;
Most commonly M is a metric space and dissimilarity is expressed as a distance metric, which is symmetric and satisfies the triangle inequality. Even more common, M is taken to be the d-dimensionalvector space where dissimilarity is measured using theEuclidean distance, Manhattan distance or other distance metric. However, the dissimilarity function can be arbitrary. One example are asymmetricBregman divergences, for which the triangle inequality does not hold.[1]
距离矩阵的度量问题;
2.方法:(遇到的问题:维数灾难;)
Linear search(适合小范围的距离计算)
The simplest solution to the NNS problem is to compute the distance from the query point to every other point in the database, keeping track of the "best so far". This algorithm, sometimes referred to as the naive approach, has a running time of O(Nd) where N is the cardinality of S and d is the dimensionality of M. There are no search data structures to maintain, so linear search has no space complexity beyond the storage of the database. Naive search can, on average, outperform space partitioning approaches on higher dimensional spaces.[2]
Space partitioning(决策树?)
Since the 1970s, branch and bound methodology has been applied to the problem. In the case of Euclidean space this approach is known asspatial index or spatial access methods. Several space-partitioning methods have been developed for solving the NNS problem. Perhaps the simplest is thek-d tree, which iteratively bisects the search space into two regions containing half of the points of the parent region. Queries are performed via traversal of the tree from the root to a leaf by evaluating the query point at each split. Depending on the distance specified in the query, neighboring branches that might contain hits may also need to be evaluated. For constant dimension query time, average complexity isO(log N)[3] in the case of randomly distributed points, worst case complexity analyses have been performed.[4] Alternatively theR-tree data structure was designed to support nearest neighbor search in dynamic context, as it has efficient algorithms for insertions and deletions.
In case of general metric space branch and bound approach is known under the name ofmetric trees. Particular examples include vp-tree and BK-tree.
Using a set of points taken from a 3-dimensional space and put into aBSP tree, and given a query point taken from the same space, a possible solution to the problem of finding the nearest point-cloud point to the query point is given in the following description of an algorithm. (Strictly speaking, no such point may exist, because it may not be unique. But in practice, usually we only care about finding any one of the subset of all point-cloud points that exist at the shortest distance to a given query point.) The idea is, for each branching of the tree, guess that the closest point in the cloud resides in the half-space containing the query point. This may not be the case, but it is a good heuristic. After having recursively gone through all the trouble of solving the problem for the guessed half-space, now compare the distance returned by this result with the shortest distance from the query point to the partitioning plane. This latter distance is that between the query point and the closest possible point that could exist in the half-space not searched. If this distance is greater than that returned in the earlier result, then clearly there is no need to search the other half-space. If there is such a need, then you must go through the trouble of solving the problem for the other half space, and then compare its result to the former result, and then return the proper result. The performance of this algorithm is nearer to logarithmic time than linear time when the query point is near the cloud, because as the distance between the query point and the closest point-cloud point nears zero, the algorithm needs only perform a look-up using the query point as a key to get the correct result.
空间划分是一个构建空间树的过程,其构建过程比较复杂,涉及到大量的计算;
Locality sensitive hashing(hash过程,可以近似O(1)的时间查询表)
Locality sensitive hashing (LSH) is a technique for grouping points in space into 'buckets' based on some distance metric operating on the points. Points that are close to each other under the chosen metric are mapped to the same bucket with high probability.[5]
Nearest neighbor search in spaces with small intrinsicdimension
The cover tree has a theoretical bound that is based on the dataset's doubling constant. The bound on search time is O(c12 log n) wherec is theexpansion constant of the dataset.
Vector approximation files
In high dimensional spaces, tree indexing structures become useless because an increasing percentage of the nodes need to be examined anyway. To speed up linear search, a compressed version of the feature vectors stored in RAM is used to prefilter the datasets in a first run. The final candidates are determined in a second stage using the uncompressed data from the disk for distance calculation.[6]
Compression/clustering based search
The VA-file approach is a special case of a compression based search, where each feature component is compressed uniformly and independently. The optimal compression technique in multidimensional spaces is Vector Quantization (VQ), implemented through clustering. The database is clustered and the most "promising" clusters are retrieved. Huge gains over VA-File, tree-based indexes and sequential scan have been observed.[7][8] Also note the parallels between clustering and LSH.
3.次优最近邻
Algorithms that support the approximate nearest neighbor search includelocality-sensitive hashing,best bin first andbalanced box-decomposition tree based search.[9]
(1):ε-approximate nearest neighbor search is a special case of thenearest neighbor search problem. The solution to the ε-approximate nearest neighbor search is a point or multiple points within distance (1+ε) R from a query point, where R is the distance between the query point and its true nearest neighbor.
Reasons to approximate nearest neighbor search include the space and time costs of exact solutions in high dimensional spaces (seecurse of dimensionality) and that in some domains, finding an approximate nearest neighbor is an acceptable solution.
Approaches for solving ε-approximate nearest neighbor search includekd-trees,Locality Sensitive Hashing andbrute force search.
(2):Best bin first is a search algorithm that is designed to efficiently find an approximate solution to the nearest neighbor search problem in very-high-dimensional spaces. The algorithm is based on a variant of thekd-tree search algorithm which makes indexing higher dimensional spaces possible. Best bin first is an approximate algorithm which returns the nearest neighbor for a large fraction of queries and a very close neighbor otherwise.[1]
Differences from kd tree:
- Backtracking is according to a priority queue based on closeness.
- Search a fixed number of nearest candidates and stop.
- A speedup of two orders of magnitude is typical. 主要是对于超大型数据库进行相似性查询;
References:Beis, J.; Lowe, D. G. (1997). "Shape indexing
using approximate nearest-neighbour search in high-dimensional spaces". Conference on Computer Vision and Pattern Recognition. Puerto Rico. pp. 1000–1006.CiteSeerX:10.1.1.23.9493.
(3):LSH:http://en.wikipedia.org/wiki/Locality_sensitive_hashingLocality-sensitive hashing (LSH) is a method of performing probabilisticdimension reduction of high-dimensional data. The basic idea is tohash the input items so that similar items are mapped to the same buckets with high probability (the number of buckets being much smaller than the universe of possible input items). This is different from the conventional hash functions, such as those used incryptography, as in the LSH case the goal is to maximize probability of "collision" of similar items rather than avoid collisions.[1] Note how locality-sensitive hashing, in many ways, mirrors data clustering andNearest neighbor search.
(二):局部敏感hash:
(三):minihash:原文链接:http://my.oschina.net/pathenon/blog/65210
转自wiki:http://en.wikipedia.org/wiki/Locality_sensitive_hashing
1.概述introduction:
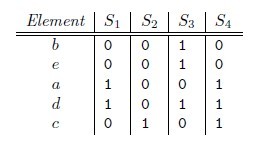
Jaccard index是用来计算相似性,也就是距离的一种度量标准。假如有集合A、B,那么,
假定h是一个将A和B中的元素映射到一些不相交整数的哈希函数,而且针对给定的S,定义hmin(S)为S集合中具有最小h(x)函数值的元素x。这样,只有当最小哈希值的并集A ∪ B依赖于交集A ∩B时,有hmin(A) =hmin(B)。 因此,
- Pr[hmin(A) =hmin(B)] =J(A,B).
另一方面来说,如果r是一个当hmin(A) =hmin(B)时值为1,其它情况下值为0的随机变量,那么r可认为是J(A,B)的无偏估计。尽管此时方差过高,单独使用时没什么用处。最小哈希方法的思想是通过平均用同一方式构造的许多随机变量,从而减少方差。
那么对集合A、B,hmin(A) = hmin(B)成立的条件是A ∪ B 中具有最小哈希值的元素也在 ∩ B中。这里有一个假设,h(x)是一个良好的哈希函数,它具有很好的均匀性,能够把不同元素映射成不同的整数。
所以有,Pr[hmin(A) = hmin(B)] = J(A,B),即集合A和B的相似度为集合A、B经过hash后最小哈希值相等的概率。
第一种:使用多个hash函数
(3):^Chum, Ond?ej; Philbin, James; Isard, Michael; Zisserman, Andrew, Scalable near identical image and shot detection, Proceedings of the 6th ACM International Conference on Image and Cideo Retrieval (CIVR'07). 2007,doi:10.1145/1282280.1282359;Chum, Ond?ej; Philbin, James; Zisserman, Andrew,Near duplicate image detection: min-hash and tf-idf weighting, Proceedings of the British Machine Vision Conference,