Canopy聚类算法分析

      原文链接：http://blog.csdn.net/yclzh0522/article/details/6839643

      Canopy聚类算法是可以并行运行的算法，数据并行意味着可以多线程进行，加快聚类速度，开源ML库Mahout使用。

一、概念    

       与传统的聚类算法(比如 K-means )不同，Canopy 聚类最大的特点是不需要事先指定 k 值( 即 clustering 的个数)，因此具有很大的实际应用价值。与其他聚类算法相比，Canopy聚类虽然精度较低，但其在速度上有很大优势，因此可以使用 Canopy 聚类先对数据进行“粗”聚类，（摘自于Mahout一书：Canopy算法是一种快速地聚类技术，只需一次遍历数据科技得到结果，无法给出精确的簇结果，但能给出最优的簇数量。可为K均值算法优化超参数..K....）得到 k 值后再使用 K-means 进行进一步“细”聚类。这种Canopy + K-means的混合聚类方式分为以下两步：

 Step1、聚类最耗费计算的地方是计算对象相似性的时候，Canopy 聚类在第一阶段选择简单、计算代价较低的方法计算对象相似性，将相似的对象放在一个子集中，这个子集被叫做Canopy ，通过一系列计算得到若干Canopy，Canopy 之间可以是重叠的，但不会存在某个对象不属于任何Canopy的情况，可以把这一阶段看做数据预处理；

 Step2、在各个Canopy 内使用传统的聚类方法(如K-means)，不属于同一Canopy 的对象之间不进行相似性计算。

      从这个方法起码可以看出两点好处：首先，Canopy 不要太大且Canopy 之间重叠的不要太多的话会大大减少后续需要计算相似性的对象的个数；其次，类似于K-means这样的聚类方法是需要人为指出K的值的，通过Stage1得到的Canopy 个数完全可以作为这个K值，一定程度上减少了选择K的盲目性。

二、聚类精度

      对传统聚类来说，例如K-means、Expectation-Maximization、Greedy Agglomerative Clustering，某个对象与Cluster的相似性是该点到Cluster中心的距离，那么聚类精度能够被很好保证的条件是：

      对于每个Cluster都存在一个Canopy，它包含所有属于这个Cluster的元素。

      如果这种相似性的度量为当前点与某个Cluster中离的最近的点的距离，那么聚类精度能够被很好保证的条件是：

      对于每个Cluster都存在若干个Canopy，这些Canopy之间由Cluster中的元素连接（重叠的部分包含Cluster中的元素）。

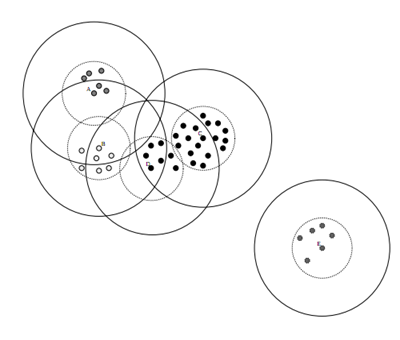
      数据集的Canopy划分完成后，类似于下图：

三、Canopy算法流程

      （1）将数据集向量化得到一个list后放入内存，选择两个距离阈值：T1和T2，其中T1 > T2，对应上图，实线圈为T1，虚线圈为T2，T1和T2的值可以用交叉校验来确定；

      （2）从list中任取一点P，用低计算成本方法快速计算点P与所有Canopy之间的距离（如果当前不存在Canopy，则把点P作为一个Canopy），如果点P与某个Canopy距离在T1以内，则将点P加入到这个Canopy；

      （3）如果点P曾经与某个Canopy的距离在T2以内，则需要把点P从list中删除，这一步是认为点P此时与这个Canopy已经够近了，因此它不可以再做其它Canopy的中心了；

      （4）重复步骤2、3，直到list为空结束。

       注意：Canopy聚类不要求指定簇中心的个数，中心的个数仅仅依赖于举例度量，T1和T2的选择。

Python代码：

#-*- coding:utf-8 -*- 
'''
'''
import numpy as np
import matplotlib as nlp

#The first op
import scipy as sp  
import scipy.sparse.linalg  
import time  
from Old_regression import crossValidation

#使用K均值
import kMeans as km

def canopyClustering(datalist):
    state =[];
    #交叉验证获取T1和T2;
    T1,T2 = crossValidation(datalist);
    #canopy 预聚类
    canopybins= canopy(datalist, T1 , T2);
    #使用K均值聚类
    k =len(canopybins);
    createCent = [canopy[0] for canopy in canopybins];#获取canopybins中心
    dataSet    = datalist；
    centroids, clusterAssment =km.kMeans(dataSet, k, distMeas=distEclud, createCent);
    return clusterAssment;

#得到一个list后放入内存，选择两个距离阈值：T1和T2，其中T1 > T2
#Canopy聚类不要求指定簇中心的个数，中心的个数仅仅依赖于举例度量，T1和T2的选择。
def canopy(datalist, T1 , T2):
    #state  = [];datalist  = [];
    #初始化第一个canopy元素
    canopyInit = datalist.pop();
    canopyCenter= calCanopyCenter([canopyInit] );
    
    canopyC = [canopyInit];#建立第一个canopy
    canopybins = [];
    canopybins.append([canopyCenter,canopyC ] );
    
    while not(len(datalist) ==0 ):
        PointNow =datalist[len(datalist)-1 ];#PointNow =datalist.pop();
        counter = 0;
        for canopy in canopybins:
            dis =calDis(PointNow, canopy[0]);
            #如果点P与某个Canopy距离在T1以内，则将点P加入到这个Canopy；
            if dis<T1:
                canopy[1].append(PointNow);
                counter +=1;
                #break;
            if dis<T2:
                #点P曾经与某个Canopy的距离在T2以内，则需要把点P从list中删除，
                #这一步是认为点P此时与这个Canopy已经够近了，因此它不可以再做其它Canopy的中心了
                if not(counter ==0):#保证必须率属于一个canopy
                    del list[len(datalist)-1 ];
                    break;
                else:#建立一个新的Canopy
                    canopyC = [PointNow];
                    canopyCenter= PointNow;
                    canopybins.append([canopyCenter,canopyC ] );
                   
    return canopybins;

def calDis(va,vb):
    dis =0;
    for i in range(len(va) ):
        dis += va[i]*va[i]+ vb[i]*vb[i];
    return dis;

#计算canopy中心
def calCanopyCenter(datalist):
    center =datalist[0];
    for i in len(range(center) ):
        center[i]=0;
        
    for data in datalist:
        center +=data;
    center /= len(center);
    
    return center;