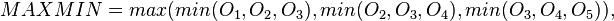图像基本群运算--滤波

       工业和消费领域，图像获取主要依赖于电子元件CMOS和CCD，以光电转化的形式转化为电信号。信号在传输的过程中会因为电信号的本身干扰，发生失真。常见的噪声有椒盐噪声、高斯白噪声等。

1、高斯白噪声

         一般性的光线教暗容易使图像产生高斯白噪声，噪声产生并非严格遵循高斯分布，一般为高斯分布的近似形式。

         一般没有明显的颗粒感，为随机噪声。

         抵消高斯噪声影响的方法一般为使用高斯平滑滤波器，高斯平滑核一般取高斯分布：

                                  F(x, y, z) = 1/2pi*u^2  *Exp(-(x^2+ y^2 ) /2*u^2 )

         一个五层高斯卷积核：

               [ 0.002              

                 0.013      0.060          

                 0.220      0.098      0.162

                                                           0.096

                                                                        0.002   ]  ，整个核为对称阵，并且轴对称...

       加速：快速卷积算法为把一次二维卷积拆成两次一维卷积，使用向量化进行并行计算。

        使用OpenCV：

        获得高斯核: Mat getGaussianKernel(int ksize, double sigma, int ktype=CV_64F );

        使用高斯核：

    Mat img, gray;
    if( argc != 2 && !(img=imread(argv[1], 1)).data) return -1;
    cvtColor(img, gray, CV_BGR2GRAY);
    GaussianBlur( gray, gray, Size(9, 9), 2, 2 );  // smooth it, otherwise a lot of false circles may be detected

2.均值滤波：

       使用一个均值滤波器来模糊图像来模糊噪声，效果当然是不太好的。

        一个三层卷积核：

               [ 1      1        1

                 1      1       1

                 1      1       1 ]  *   1/9

        使用OpenCV：C++:    void medianBlur(InputArray src, OutputArray dst, int ksize)

3.椒盐噪声：

       也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的孤立白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。盐和胡椒噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误（传输干扰、解码误差）等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。

        转自于 维基：

       
       

       常用的去除这种噪声的有效手段是使用中值滤波器。下面的实例图像分别是原始图像、带有椒盐噪声的图像、经过平均滤波器修复的图像以及经过中值滤波器修复的图像。

       效果：凭视觉感受一下椒盐的颗粒大小Pixels，把中值滤波器的卷积核的Pixels个中间像素设置为0，一般能达到效果。

       一个三层卷积核：

               [ 1      1        1

                 1       0       1

                 1      1        1 ]  *   1/8

                                                                                                                                                                                 

非线性处理方式

一般使用非线性滤波器处理椒盐噪声的方法，以下将简介三种解决方法。

异常值侦测

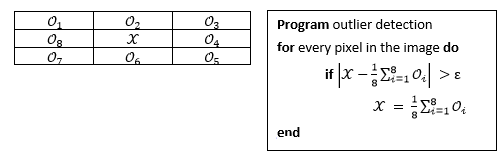
异常侦测（Anomaly detection）有时称为异常值侦测（Outlier detection），如其名所隐含的，在给定的资料集合中，它将侦测在已有的规律中表现异常者。现今常用的方法以计算距离为基础的K-近邻算法或是机器学习中的支持向量机等，下图的例子以平均数为基础，在3X3的遮罩中，计算每个像素的平均值，与平均值相差绝对值ε的像素值将被平均值取代，其中，遮罩大小和误差值ε则是和输入图片内容相关。

Outlier detection的缺点在于用平均值替代像素值，会造成像素值单一的背景出现异常的杂点（如天空），虽然相较于原本的盐与胡椒噪声不明显，但仍然可以看出噪声。

中值滤波器

中值滤波器（Median filtering） 如其名所隐含的，它将一个像素的值用该像素邻域中强度值的中间值来取代（计算中间值的过程中，也会将该像素的原始值包含），中值滤波器在处理盐和胡椒噪声上能提供绝佳的噪声降低效能。中值滤波器所衍伸的问题是计算速率，举例而言，要计算5个元素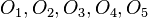的中值滤波器的计算过程如下：

       

    

          先取最小值再取最大值可以得到中间值，但做最小值的过程中，需要先考虑10个可能的选项（），由于计算速度的考量，因此促进了Pseudo-median filtering (PMED)的产生。 中值滤波器的缺点为让边缘模糊、较不锐利，由于使用中间值替代向素值，在像素值容易有较大变化的地方，如边界或细节的地方，会被模糊。

伪中值滤波器

为了改进中值滤波器的计算速率，伪中值滤波器（Pseudo-median filtering） 以近似的方法算出中间值，以5个元素的伪中值滤波器为例，

          

其中，MAXMIN会低估中间值，而MINMAX会高估中间值，将两者平均起来以近似中间值。应用在2D的伪中值滤波器可以有许多取法，例如：

            

          

4.双边滤波器

         参考：http://blog.csdn.net/abcjennifer/article/details/7616663

        源于高斯模糊方法，用于保边去噪。方法为：当亮度差值过大时，通过下降滤波器权重来防止边界模糊，算是一个动态滤波器。

Matlab实现保边滤波器的函数是：　　

w = 5;       % bilateral filter half-width  
sigma = [3 0.1]; % bilateral filter standard deviations
N =double(Img)/255; 
S =bfilter2(N,w,sigma);

OpenCV实现保边滤波器的函数是：

int d=2; 
double sigmaColor=0.1; double sigmaSpace=0.3;
int borderType = BORDER_DEFAULT;
Mat pFilterMatB = Mat(Size(pGrayMat.rows, pGrayMat.cols), CV_8SC1);

cv::bilateralFilter(pGrayMat, pFilterMatB, d, sigmaColor, sigmaSpace, borderType);

5、实验结果：

参考链接：图像滤波常见方法原理总结及VC下实现

    

    自己写的Conv2滤波器效果还是不如Matlab,差距太明显了...