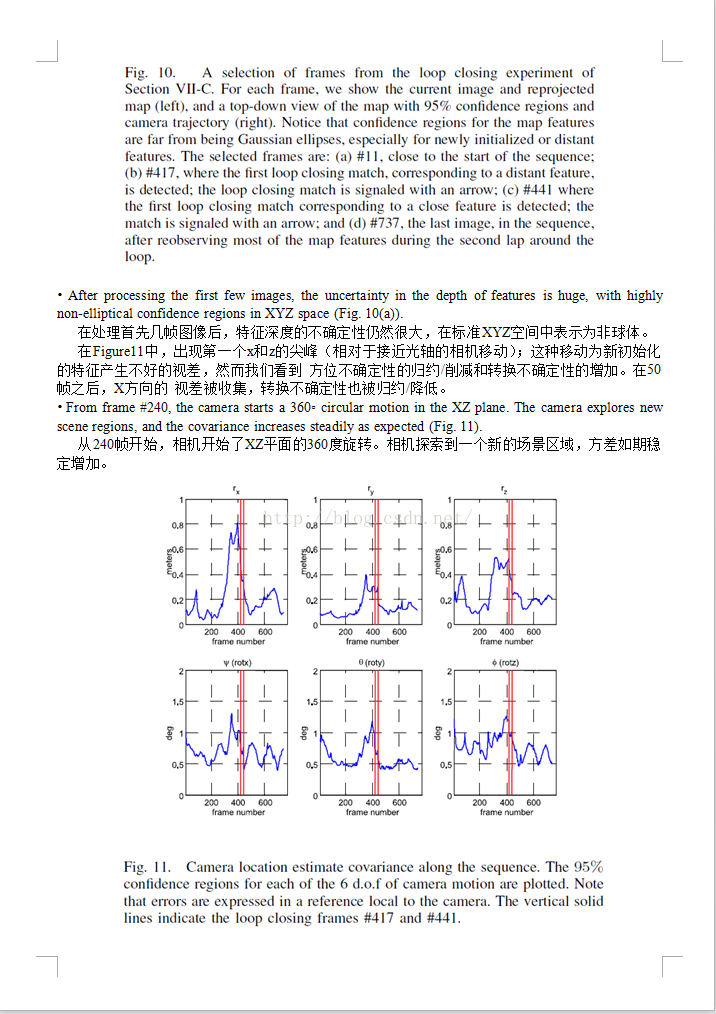
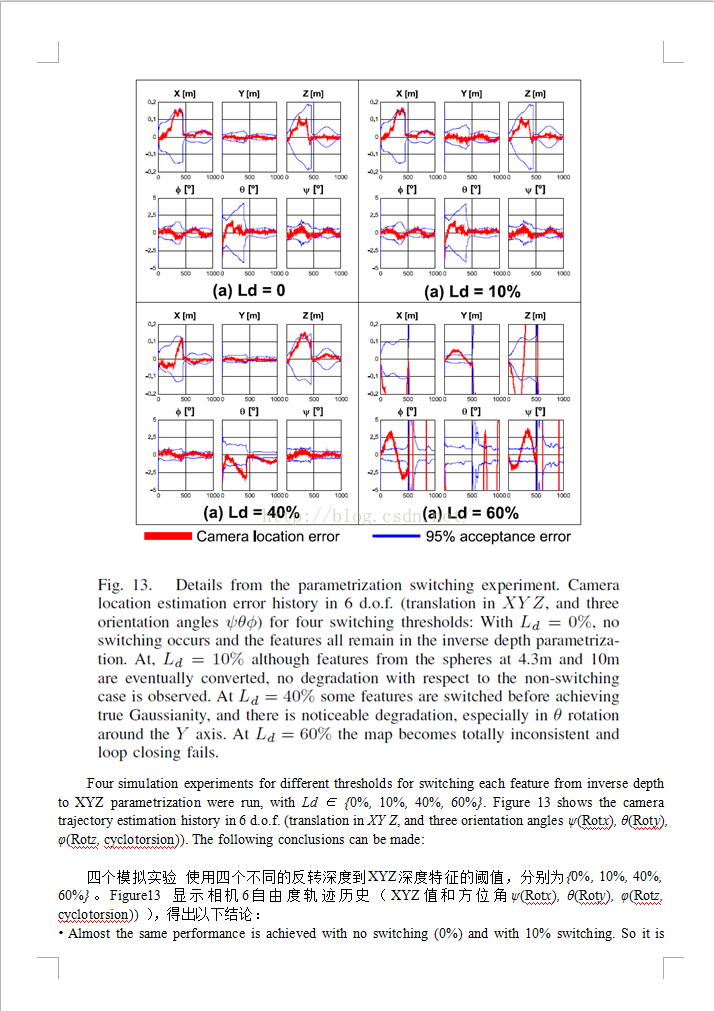
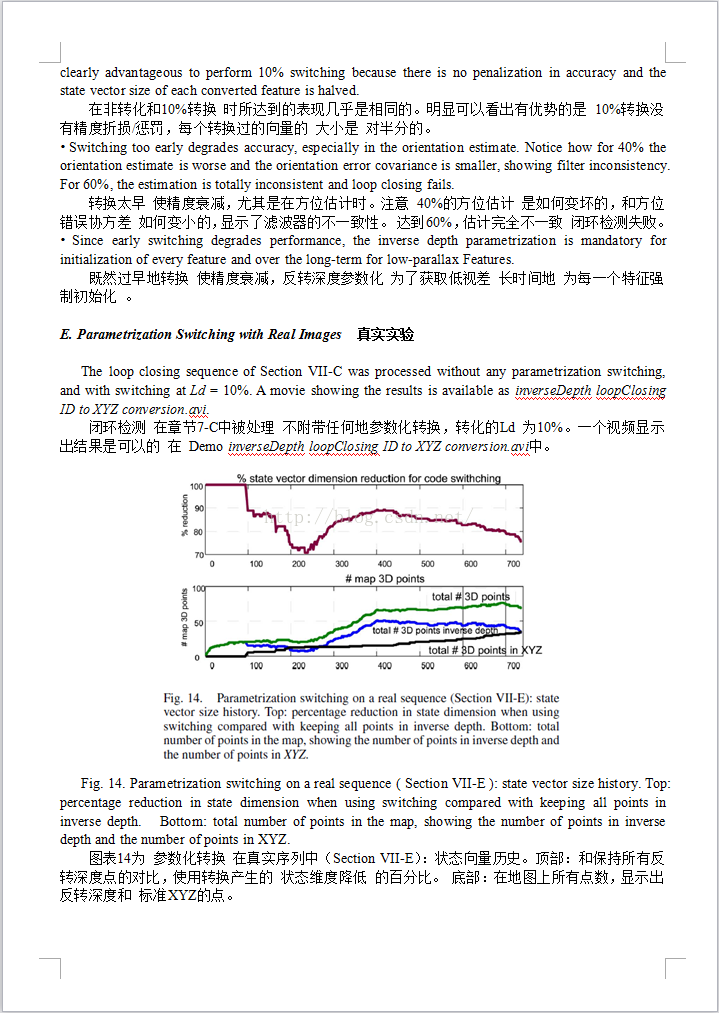
SLAM: Inverse Depth Parametrization for Monocular SALM

首语：

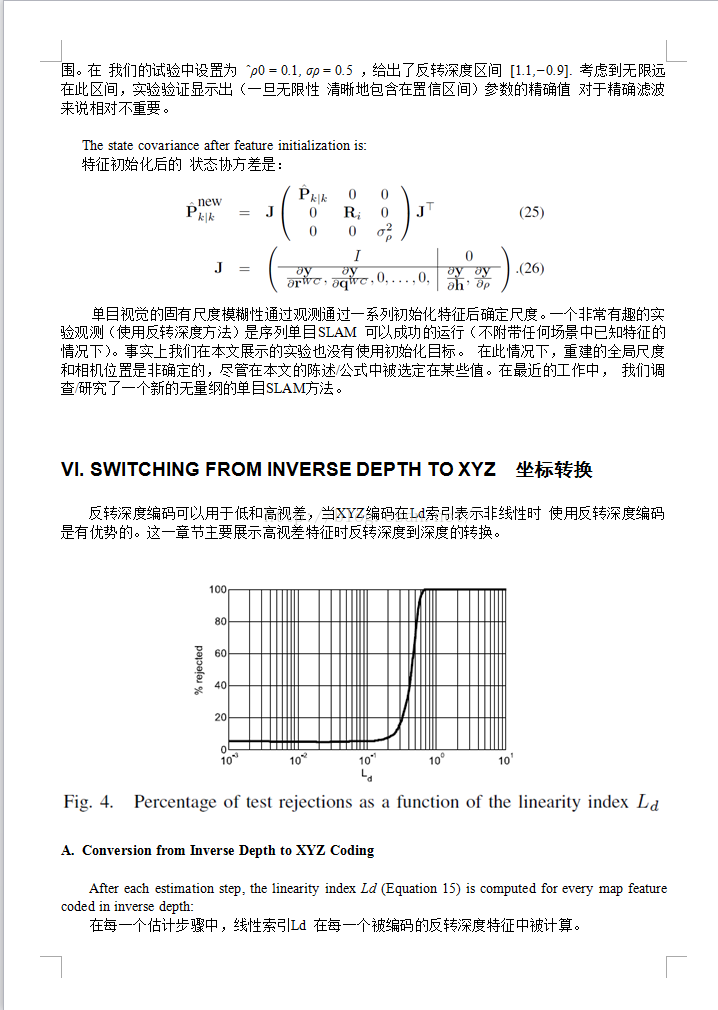
          此文实现客观的评测了使线性化的反转深度的效果。整篇只在表明反转可以线性化，解决距离增加带来的增长问题，有多少优势……%！

          我的天呢！我竟然完整得翻译了一遍。

        使用标记点地图构建SLAM的方法，有一种EKFmonocularSLAM的存在，可以不使用BA直接完成稀疏场景地图重建，详细方法和代码见官网：http://www.openslam.org/

        EKF-SLAM使用EKF方法，所使用的方法参考两篇论文：

Long Description
        This code contains a complete EKF SLAM system from a monocular sequence, taking as input a sequence from a monocular camera and estimating the 6 DOF camera motion and a sparse 3D map of salient point features. The key contributions in this code are two:

        1)  INVERSE DEPTH POINT PARAMETRIZATION. This point model suits the projective nature of the camera sensor, allowing to code in the SLAM map very distant points naturally captured by a camera. It is also able to code infinite depth uncertainty, allowing undelayed initialization of point features from the first frame they were seen. At any step, the measurement equation shows the high degree of linearity demanded by the EKF.

        2)  1-POINT RANSAC. Robust data association has proven to be a key issue in any SLAM algorithm. 1-Point RANSAC is an algorithm based on traditional random sampling but adapted to the EKF. Specifically, it exploits probabilistic information from the EKF to greatly improve the efficiency over standard RANSAC.

       本文翻译第一篇：《 nverse Depth Parametrization for Monocular SALM 》

Inverse Depth Parametrization for Monocular SLAM
Javier Civera, Andrew J. Davison, J.M.M Montiel, Member, IEEE

Abstract

     We present a new parametrization for point features within monocular SLAM which permits efficient and accurate representation of uncertainty during undelayed initialisation and beyond, all within the standard EKF (Extended Kalman Filter). The key concept is direct parametrization of the inverse depth of features relative to the camera locations from which they were first viewed, which produces measurement equations with a high degree of linearity. Importantly, our parametrization can cope with features over a huge range of depths, even those which are so far from the camera that they present little parallax during motion — maintaining sufficient representative uncertainty that these points retain the opportunity to ‘come in’ smoothly from infinity if the camera makes larger movements. Feature initialization is undelayed in the sense that even distant features are immediately used to improve camera motion estimates, acting initially as bearing references but not permanently labeled as such.
     The inverse depth parametrization remains well behaved for features at all stages of SLAM processing, but has the drawback in computational terms that each point is represented by a six dimensional state vector as opposed to the standard three of a Euclidean XYZ representation. We show that once the depth estimate of a feature is sufficiently accurate, its representation can safely be converted to the Euclidean XYZ form, and propose a linearity index which allows automatic detection and conversion to maintain maximum efficiency — only low parallax features
need be maintained in inverse depth form for long periods. We present a real-time implementation at 30Hz where the parametrization is validated in a fully automatic 3D SLAM system featuring a hand-held single camera with no additional sensing. Experiments show robust operation in challenging indoor and outdoor environments with very large ranges of scene depth, varied motion and also real-time 360 ◦ loop closing.

 Index Terms—Real-time vision, monocular SLAM.实时视觉，单目视觉。

    本文为单目SLAM方法 提出一个 点特征参数化的 新方法， 使用标准EKF方法为非延迟初始化完成有效和精确的表示。主要内容是（涉及到 初次探测的相机位置/世界坐标系）直接参数化 ，产生一个高度线性的测量方程。 重要的是，我们的方法可以处理长程/长距离的特征，甚至一些远到 移动期间视差很小的运动——并可维持 有效地表达 典型非确定性（在非特定情况下的有效表达）——若相机有一个长距离的移动（从离相机无限远平滑地接近）。在需要即时进行提升相机估计的场景中可以做到无延迟的特征初始化，只是作为对照引用而非永久标记。

    深度反转参数法在SLAM过程中所有的阶段 保持良好的运行，但是在 计算(方面) 与 标准XYZ欧式表达相反 的标记六自由度状态向量的每一个点（对比）时仍有缺点。 我们表明 一旦特征的深度估计 足够精确， 其表示可以安全地转换为标准欧式XYZ形式，并且 提出/生成 一个允许可保持最大效率的 自动探测和转换——在相当长的时间内 只需要需要保留 很少的并行特征用于深度生成。 我们提出一个 实时的 可以达到30Hz（用于在自动3D场景SLAM过程）--单目手持（不附带额外场景模式）的稳固的参数化过程 。实验显示算法在室内/室外场景中在360度闭环检测中具有鲁棒性。

I. INTRODUCTION

     单目摄像机是一个测量系列图像投影的设备。给出移动摄像获得的， 一个3维刚体物体的序列图像，可以根据 一个比例因子 同时计算出整个场景和摄像机的移动。摄像机必须重复地观测一个物体，每次获取物体影像到图像光心。从不同的视角获取的图像，计算出的（测定）的角度 为特征的视差——这就是允许/用于深度估计的参数。

    在离线SFM（移动中重建）文献的解决方案(e.g. [11], [23])中，移动和结构从一系列图像中被估计（ 利用相邻成对图像中的鲁棒特征 估计运动相关性)。然后一个优化方法 迭代地更新估计全局相机位置和场景特征位置（以至于特征投影尽可能地靠近他们的测量位置（光束法平差） ）。本着这种精神/源自于此种精髓 的一些方法 使用了滑窗过程替代全局优化，得到/演变出令人印象深刻的 “视觉里程法”解决方案， 已应用于立体图像序列[21] 和单目图像序列 [20]（构建）。

    达到实时SFM的另一个途径是在线SLAM方法， 利用一个概率滤波进行位置特征序列（地图）和摄像机角度位置 的更新。SLAM方法相对于视觉里程法有特定的优势和弱点，能够利用有限的地图特征构建连续和无漂移的全局地图。核心算法为扩展卡尔曼滤波，（此方法）在多传感器机器人中被证明，首次被应用于Davison et al. [8] [9] 实时单目重建 ，其可以进行30Hz的稀疏重建。

    Davison’s 方法和类似方法的一个局限是，他们只能处理 小幅度相机-距离变化的图像特征，并且要求具有显著的视差。此问题在 非确定性深度估计（远距离特征被初始化）：采用 直接欧式XYZ方法参数化，当高斯分布应用于 EKF方法时 造成的位置不确定性的小视差特征，不能被较好地表达。这些特征的深度坐标有一个概率密度， 能明显增强一个良定义的小深度值的尖峰，然而随后逐渐缩小到无穷远（以/从一个小视差测量）， 这很难给出是否一个特征拥有10 个单位而不是100个、1000个或者更多。随后的论文中我们偏向于直接的欧式XYZ坐标的使用。？？？

     最近有一些较新的方法提出用于解决此类问题，依赖于（不被普遍需要的）新的特征。在此文中，我们提出一个新的特征参数化方法 能都平滑的用于所有深度的特征初始化——甚至是“无穷远”，并直接使用标准EKF框架。关键内容是使用与摄像机位置相关的（第一次被）首先被观测到特征 进行直接参数化。

A. Delayed and Undelayed Initialization  何时初始化？延迟还是不延迟？

    最常见的处理特征初始化的方法是，将处理新探测到的特征汇 从主地图中抽离，在/从特定过程中（在嵌入整个使用标准XYZ表达的滤波器之前）从几帧图像中收集信息降低不确定性。这种延迟初始化策略 (e.g. [8], [14], [3])有一样缺陷 ：维持在主要概率状态之外的新特征，不能够 对最终地图中的相机位置估计做出贡献（对 会存在的最终的地图中的相机位置估计没有效果）。更深刻地说，那些多帧仍持有较低视差的特征（那些远离摄像机的块，或者靠近移动 核/极点位置的块）通常会被完全拒绝掉， 因为不能通过包含(可利用)测试？

    在延迟方法中Bailey [2]，初始化被推迟直到测量方程接近高斯，且点可以安全地被三角化时。如在2D中被提出和在模拟实验中被验证的，一个相似的方法（附有惯性传感器的3D视觉）被提出 [3]， Davison引用一个新的特征[8]（通过 嵌入一个3D半无限雷达 到主 地图（表示了除了深度以外的各种特征） ），然后使用一个辅助粒子滤波器经过几帧去清晰地更新深度，利用了高帧率序列的所有测量（除了在主状态之外的状态向量）。

    更近一段时间，几个非延迟初始化的方法被提出，依然是使用一些特殊方法处理新进特征但 能够立刻对摄像机位置估计产生效用，主要视角是 尽管带有高度非确定深度的特征 对于估计相机转换 提供的信息太少，但对方向估计有极大的as轴承/参考的作用。非延迟方法为Kwok and Dissanayake所提出 [15] ，是一个多假设方法，初始化特征到多深度，并在子序列未被观察时进行剪枝。

    Sola et al. [25], [24] 描述了一个更为严格的非延迟方法 使用一个近似高斯和滤波器（通过联合信息）使保持计算负载较低。一个重要的视点是扩展高斯深度假设（通过反转深度到ray方向射线），在此方式上得到更好的表达。这种方法可能是 Davison的粒子算法和我们的反转深度方法的垫脚石。(一个)高斯和 是比粒子更为有效的表达（足够有效到各自的高斯可以被放入主状态向量），但仍然不如单个的（使用反转深度参数化的）高斯表达 ；注意的是 [15] nor [25] 考虑特征在一个非常大的 “无限的”深度。

B. Points at Infinity 无限远点

    本文的一个主要动机/推进/改进 不仅是非延迟初始化，还包括处理所有深度的特征的需求，尤其是在室外场景。在SFM中，无穷远点在相机变换时是表示为无视差的（因其为极限深度）。比如一个星星可能在一个图像中表示为一个位置（尽管其在数千里之外移动了数千米）。这样的特征不能被使用用于估计相机变化，但可以作为一个完美的轴承/参考用于旋转估计。视觉投影几何 的齐次坐标系（被正常使用 在SFM中的）可以清晰地表示无穷远点， 并且在离线构建和姿态估计中 表示为一个 重要的角色。

     在序列SLAM系统中，困难是 我们并不预先知道那些特征是无穷远的，Montiel and Davison [19]表示在特定的情况下所有的特征被认为是无穷远的。——在大范围的室外场景或者相机在三角桌上旋转时，SLAM在纯角度/极坐标系表现为实时摄像机视觉罗盘。     在更一般的场合，让我们想象一个相机穿越一个3D场景（即观测一个长程的深度特征）。从点的视角估计开始，我们可以认为所有的特征从无限远开始，并且“接近” （随着摄像机移动的足够远到）直到可以测量有效的视差。    在室内的场景中，仅仅几分米的距离便足够有效。远距特征可能要求更多的米数或者数千米（在视差被观测到之前），重要的是这些特征是并非长久地标记——一个看似无穷远的特征， 应当一直有机会（通过移动足够的距离）证明他的无限远深度，否则在建立场景地图时将会产生严重的同步错误。    我们的概率SLAM算法应当能够表达看起来无限远的深度的非特定性。在摄像机变化10个单位之后（若是特征比我们可以观测到的视差更近）仍然观测不到误差，其不能告诉我们关于深度的任何信息—（他给出了可信赖的更低的边界——这又依赖于相机造成的移动的数量）。这种对非确定性的清晰考虑并不被离线算法事先要求，但是对(实现起来)更困难的在线算法 非常重要。

C. Inverse Depth Representation 反转深度表达

       Our contribution is to show that in fact there is a unified and straightforward parametrization for feature locations which can handle both initialisation and standard tracking of both close and very distant features within the standard EKF framework.An explicit parametrization of the inverse depth of a feature along a semi-infinite ray from the position from which it was first viewed allows a Gaussian distribution to cover uncertainty in depth which spans a depth range from nearby to infinity, and permits seamless crossing over to finite depth estimates of features which have been apparently infinite for long periods of time.  The unified representation means that our algorithm requires no special initialisation process for features. They are simply tracked right from the start, immediately contribute to improved camera estimates and have their correlations with all other features in the map correctly modeled. Note that our parameterization would be equally compatible with other variants of Gaussian filtering such as sparse information filters.

    我们的贡献是揭示事实上 对于特征定位（可以使用标准EKF框架 同时进行初始化和对近距离与极远距离的标准追踪）有一致（标准的）和直接的测参数化方法。一个清晰地对来自于正无穷半轴的特征的参数化（  这一句太长了，翻译不了...）               。统一的表达意味着我们的算法不要求对特征进行特别的初始化过程。特征一般从开始即被追踪，立刻起作用于提升相机估计和正确对地图建模的所有特征的联系。 值得注意的是：我们的参数化过程能够平稳兼容高斯滤波比如稀疏信息滤波器。

    我们引入线性索引并使用它分析和提升 对于全部低和高视差的深度反转特征的表达能力。深度反转算法的唯一的缺陷是: 不断增长的状态向量（我艹，不能丢帧吗），因为反转深度参数点需要记6个参数 而不是3个XYZ编码。作为此问题的解决方案，我们展示了我们的线性索引（当特征可以安全地从反转深度到标准XYZ 时,也可应用于XYZ参数化到信号）。反转深度表达可以因此应用于小视差特征情形（当XYZ编码从高斯分离时）。值得注意的是：这种“转换”，不像延迟初始化方法，能够直接减少计算负担。(此时)SLAM精度带有或者没有转换方法的效果是一样的。

    事实上一个摄像机的投影性质意味着，图像测量过程是接近线性的（在反转深度坐标系中）（注释：一个距离-大小反比关系）。反转深度图像是一个在计算机视觉中广泛应用的概念：被译为图像差别和点的深度。 在立体视觉中：被译为 （相对于无限远中的平面的）视差（在[12]）. 反转深度图像也用于表示被场景点集包含的相机移动速率（在光流分析法中）。在追踪社区中，“修改后的极坐标系[1] ”依然探索了深度反转表达的线性属性（轻度不同但紧密相关的）问题：TMA 利用纯相位法传感器 （获得的已知运动）收集（到的）测量数据 做目标运动分析。

    However, the inverse depth idea has not previously been properly integrated in sequential, probabilistic estimation of motion and structure. It has been used in EKF based sequential depth estimation from camera known motion [16] and in multibaseline stereo Okutomi and Kanade [22] used the inverse depth to increase matching robustness for scene symmetries; matching scores coming from multiple stereo pairs with different baselines were accumulated in a common reference coded in inverse depth, this paper focusing on matchingrobustness and not on probabilistic uncertainty propagation. In [5] Chowdhury and Chellappa proposed a sequential EKF process using inverse depth but this was some way short of full SLAM in its details. Images are first processed pairwise to obtain a sequence of 3D motions which are then fused with an individual EKF per feature.

     然而，反转深度图像没有被正确的在序列图像、运动和结构估计中融合使用。被应用于基于EKF的从已知摄像机移动进行序列深度图像估计[16]，在多基线立体视觉中Okutomi and Kanade [22]使用深度反转图像去增加场景均匀匹配的鲁棒程度。匹配得分 来自于从多基线收集的（在反转深度中统一参考编码的）多立体对。这篇文章聚焦于匹配鲁棒性而不是概率不确定性推导/传播。在 [5] Chowdhury and Chellappa 提出一个序列EKF过程(使用反转深度)，但这只是SLAM过程中的一部分。从被首先处理的图像对得到一个3D运动，融合到每个特征特定的EKF状态。

    我们的与位置有关的反转深度图像的参数化（从首先被观测到的特征）意味着高斯表达（必须）是特别地良表现的，这也是为什么在SFM的齐次坐标系中的单目SLAM的直接参数化不能给出一个好的结果。这些表示只能有效地表达（相对于坐标原点的）相对无限的点集。可以这样说 我们定义的投影主体是独立的，但对于每帧特征是相关的。另外一个有趣的对比是在我们的方法中间，每个被首先观测到的包含相机位置的特征的表达和（平滑地/全局SLAM 方法的）所有的/历史的传感器的位姿估计被维持在一个滤波器中。

    两个其他作者最近出版的文章 使用了与我们相似的方法。Trawny and Roumeliotis 在 [26]提出一个非延迟的初始化 为2D单目SLAM 编码方式为一个三维点编码为两个投影射线。这种表达是过参数化的但允许非延迟初始化和编码近距远距特征，这个方法可用于同步验证结果。

    Eade and Drummond 为单目视觉提出了一个深度反转方法[10] （使用他们的Fast SLAM-based system 的内容），给出了一些声明（关于我们线性化的优势）。每一个添加到地图的新的部分初始化的特征的位置（通过 相对于初次观察到的三坐标系（世界坐标系） 在各个方向上进行初始化，然后三坐标系更新（通过每一个地图粒子的一系列卡尔曼滤波 进行更新）。 若是反转深度估计崩溃/失效，则特征转化为全初始化的标准XYZ表达。当保留的部分特征和全初始化的特征不同时，  使用部分初始化特征( 带有未知深度信息 ) 提高Camera方向和转移估计（通过一个空间向量 更新步骤）。 他们的方法明显适合 FastSLAM方法的执行，然而缺少(类似于我们文章中的)令人满意的统一/标准 的参数化方法（的质量）——（部分初始化到全部初始化 不需要清晰地固定  所有用法，都是自动的且由可观测到的测量信息组成）。

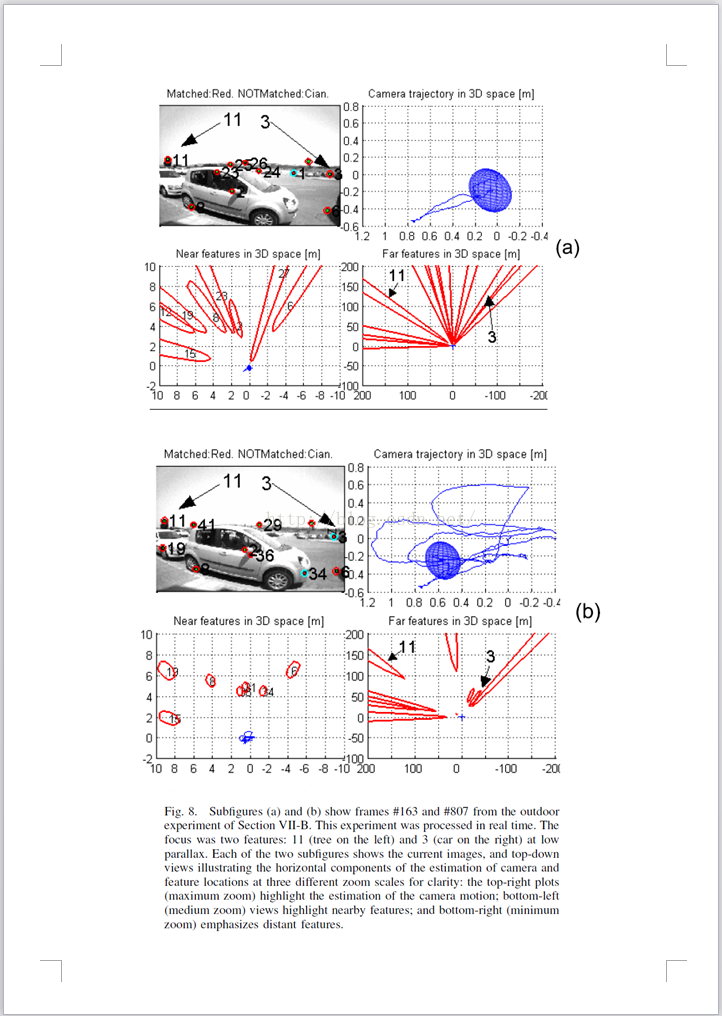
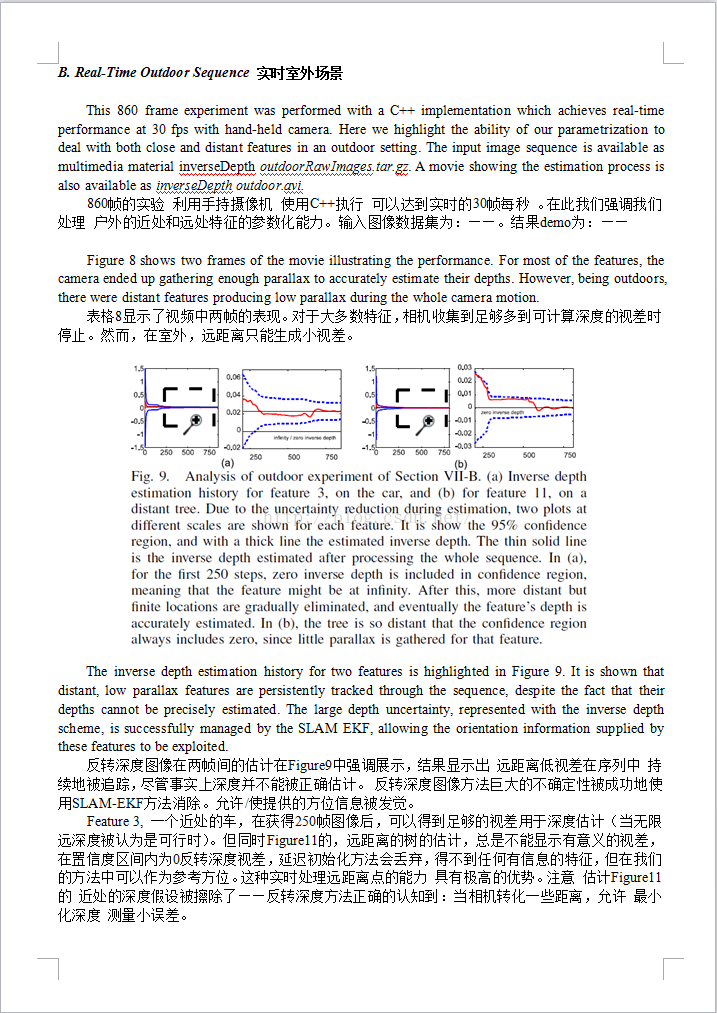
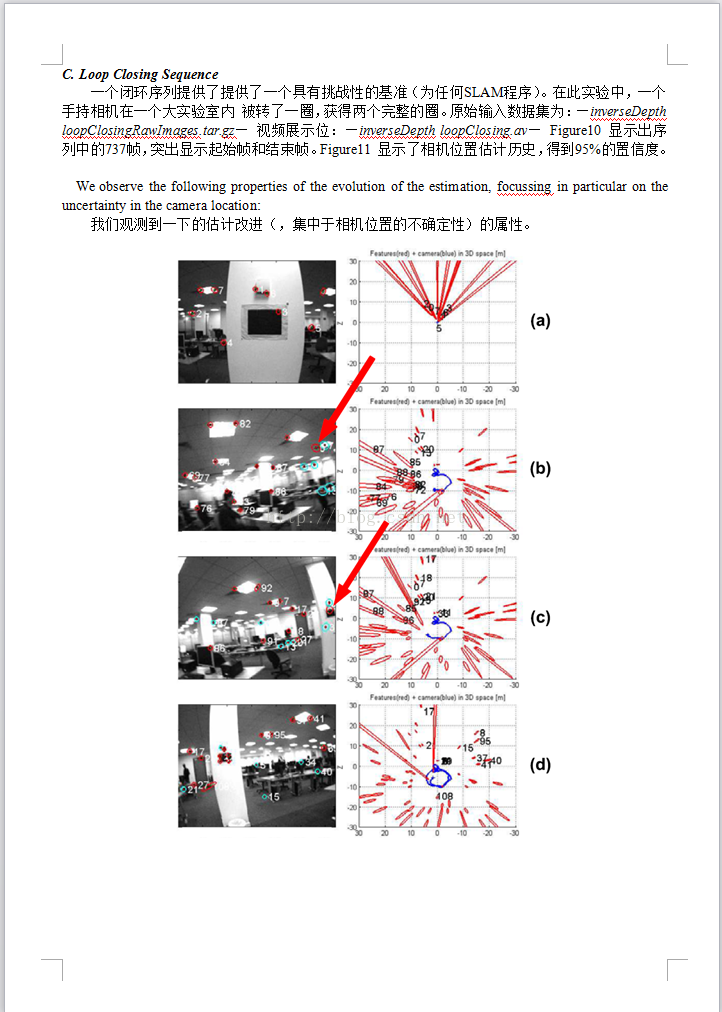
    本文提供了一个综合的/广泛地和扩展的视野（相对于我们前两篇出版的论文[18] [7]）。我们现在提出一个全实时性的 深度反转参数化的执行过程，可以达到50-70个特征（在台式机上实时运行时）。实验验证显示出精确的相机标定的重要性，可以提高系统表现尤其是对于广角摄像机。我们的结果章节 包含了一个实时的实验，包括 闭环检测的（主要结果）。输入测试图像序列和显示计算解决方案的视频 作为多媒体材料 附加在论文里。

    第二部分专注于定义一个状态向量，包括相机移动模型。XYZ点编码和反转深度点参数化，测量方程在第三部分被描述。第四部分陈述了一个讨论关于测量方程的线性误差。接着，一个特征的特征初始化细节在第五部分。在第六部分陈述反转深度到标准XYZ，在第七部分我们陈述了实际图像序列的实验验证 以30H的频率(在大范围环境中)，包括了实时实验和一个闭环检测实验。并提供指向视频的链接。最后第八部分全文总结。

REFERENCES

[1] V. J. Aidala and S. E. Hammel, “Utilization of modified polar coordinates for bearing-only tracking,” IEEE Trans. Autom. Control, vol. 28, no. 3,pp. 283–294, Mar. 1983.

[2] T. Bailey, “Constrained initialisation for bearing-only SLAM,” in Proc. IEEE Int. Conf. Robot. Autom., Taipei, Taiwan, R.O.C., Sep. 14–19, 2003, vol. 2, pp. 1966–1971.

[3] M. Bryson and S. Sukkarieh, “Bearing-only SLAM for an airborne vehicle,” presented at the Australasian Conf. Robot. Autom. (ACRA 2005),Sydney, Australia.

[4] G. C. Canavos, Applied Probability and Statistical Methods. Boston, MA: Little, Brow, 1984.

[5] A. Chowdhury and R. Chellappa, “Stochastic approximation and ratedistortion analysis for robust structure and motion estimation,” Int. J. Comput. Vis., vol. 55, no. 1, pp. 27–53, 2003.

[6] J. Civera, A. J. Davison, and J.M.M.Montiel, “Dimensionless monocular SLAM,” in Proc. 3rd Iberian Conf. Pattern Recogn. Image Anal., 2007, pp. 412–419.

[7] J. Civera, A. J. Davison, and J. M. M. Montiel, “Inverse depth to depth conversion for monocular SLAM,” in Proc. Int. Conf. Robot. Autom., 2007, pp. 2778–2783.

[8] A. Davison, “Real-time simultaneous localization and mapping with a single camera,” in Proc. Int. Conf. Comput. Vis., Oct. 2003, pp. 1403– 1410.

[9] A. J. Davison, I. Reid, N.Molton, and O. Stasse, “Real-time single camera SLAM,” IEEE Trans. Pattern Anal.Mach. Intell., vol. 29, no. 6, pp. 1052– 1067, Jun. 2007.

[10] E. Eade and T. Drummond, “Scalable monocular SLAM,” in Proc. IEEE Conf. Comput. Vis. Pattern Recogn. Jun. 17–22, 2006, vol. 1, pp. 469–476.

[11] A. W. Fitzgibbon and A. Zisserman, “Automatic camera recovery for closed or open image sequences,” in Proc. Eur. Conf. Comput. Vis., Jun. 1998, pp. 311–326.

[12] R. I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, 2nd ed. Cambridge, U.K.: Cambridge Univ. Press, 2004.

[13] D. Heeger and A. Jepson, “Subspace methods for recovering rigid motion I: Algorithm and implementation,” Int. J. Comput. Vis., vol. 7, no. 2, pp. 95–117, Jan. 1992.

[14] J. H. Kim and S. Sukkarieh, “Airborne simultaneous localisation and map building,” in Proc. IEEE Int. Conf. Robot. Autom. Sep. 14–19, 2003, vol. 1, pp. 406–411.

[15] N. Kwok and G. Dissanayake, “An efficient multiple hypothesis filter for bearing-only SLAM,” in Proc. IROS, 28 Sep.–2–Oct. 2004, vol. 1,pp. 736–741.

[16] L. Matthies, T. Kanade, and R. Szeliski, “Kalman filter-based algorithms for estimating depth from image sequences,” Int. J. Comput. Vis., vol. 3, no. 3, pp. 209–238, 1989.

[17] E. Mikhail, J. Bethel, and J. C. McGlone, Introduction to Modern Photogrammetry.New York: Wiley, 2001.

[18] J. Montiel, J. Civera, and A. J. Davison, “Unified inverse depth parametrization for monocular SLAM,” presented at the Robot. Sci. Syst. Conf., Philadelphia, PA, Aug. 2006.

[19] J. Montiel andA. J.Davison, “A visual compass based on SLAM,” in Proc. Int. Conf. Robot. Autom., Orlando, FL,May 15–19, 2006, pp. 1917–1922.

[20] E. Mouragnon, M. Lhuillier, M. Dhome, F. Dekeyser, and P. Sayd, “Realtime localization and 3-D reconstruction,” in Proc. IEEE Conf. Comput. Vis. Pattern Recogn., 2006, vol. 3, pp. 1027–1031.

[21] D. Nister, O. Naroditsky, and J. Bergen, “Visual odometry for ground vehicle applications,” J. Field Robot., vol. 23, no. 1, pp. 3–26, 2006.

[22] M. Okutomi and T. Kanade, “A multiple-baseline stereo,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 15, no. 4, pp. 353–363, Apr. 1993.

[23] M. Pollefeys, R. Koch, and L. Van Gool, “Self-calibration and metric reconstruction inspite of varying and unknown intrinsic camera parameters,” Int. J. Comput. Vis., vol. 32, no. 1, pp. 7–25, 1999.

[24] J. Sola, “Towards visual localization, mapping and moving objects tracking by a mobile robot: A geometric and probabilistic approach,” Ph.D. dissertation, LAAS-CNRS, Toulouse, France, 2007.

[25] J. Sola, A. Monin, M. Devy, and T. Lemaire, “Undelayed initialization in bearing only SLAM,” in Proc. 2005 IEEE/RSJ Int. Conf. Intell. Robots Syst., 2–6 Aug., 2005, pp. 2499–2504.

[26] N. Trawny and S. I. Roumeliotis, “A unified framework for nearby and distant landmarks in bearing-only SLAM,” in Proc. Int. Conf. Robot. Autom., May 15–19, 2006, pp. 1923–1929.