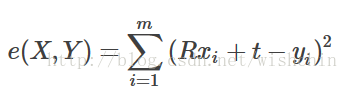三维重建10：点云配准和点云匹配

         点云的配准一般分为等价集合和律属集合两种配准，其中等价集合配准叫做匹配过程，律属集合配准被称为Alignment。

        点云的匹配一般使用ICP方法（  ICP：Iterative Closest Point迭代最近点），即两个点云纯粹通过刚体位姿变换即可大致重合，参考三维点集拟合：平面拟合、RANSAC、ICP算法。

        若找稠密/稀疏点的匹配关系，ICP算法即简化成一个最小二乘问题，可以通过解方程的方法得到解析解，使用优化方式迭代求解则一定可以得到全局最优解。若没有匹配关系，纯粹的迭代最近点方法也能得到一个极值结果，但不一定是最优的。

ICP的求解方法：

         把ICP方法看做一个点云位姿变换的过程，可以使用代数方法和非线性优化方法。

          假设有两堆点云，分别记为两个集合X=x1,x2,...,xm和Y=y1,y2,...,ym（m并不总是等于n）。

           ICP公式为：

         

1.SVD等代数方法

         先构建误差矩阵，构建最小二乘问题，求使得误差平方和最小的点云旋转和位移R，T。

         初始化估计：ICP发展了多年之后，当然有很多的方法来估计初始的R和t，PCL自己的函数 SampleConsensusInitalAlignment 函数以及TransformationEstimationSVD函数 都可以得到较好的初始估计。

         优化：得到初始化估计之后仍然存在误差问题，RANSAC之后，若已存在完全正确匹配，则可以再次求取旋转的essential矩阵，通过SVD分解得到最终旋转R和平移t。

2.非线性优化方法

         RANSAC算法之后，去除掉 外点之后。

         使用位姿的代数变化转换构建一个误差项，在非线性优化过程中不停地迭代，一般能找到极小值。

3.PCL的ICP方法

code:

// A translation on Z axis (0.4 meters)
  transformation_matrix (2, 3) = 0.4;

  
// Executing the transformation
  pcl::transformPointCloud (*cloud_in, *cloud_icp, transformation_matrix);
  *cloud_tr = *cloud_icp;  // We backup cloud_icp into cloud_tr for later use

  // The Iterative Closest Point algorithm
  time.tic ();
  pcl::IterativeClosestPoint<PointT, PointT> icp;
  icp.setMaximumIterations (iterations);
  icp.setInputSource (cloud_icp);
  icp.setInputTarget (cloud_in);
  icp.align (*cloud_icp);
  icp.setMaximumIterations (1);  // We set this variable to 1 for the next time we will call .align () function
  std::cout << "Applied " << iterations << " ICP iteration(s) in " << time.toc () << " ms" << std::endl;

transformation_matrix = icp.getFinalTransformation ().cast<double>();

Alignment方法：

PCL链接：http://pointclouds.org/documentation/tutorials/template_alignment.php#template-alignment

        Alignment分特殊情况即目标单侧面匹配，即是确定可见面对应目标物体的位姿。此种方案有多种解决方法，可以划分到物体位姿识别的范畴，使用位姿识别的通用方法来完成Alignment。

        Alignment的通常情况是可见面是目标物体的一部分，并非单侧面全覆盖，同时对应了单侧面被遮挡的状况，此种平凡状态使用不同于位姿识别的简单方法。一般使用体素化降采样，先找到大致可能的位姿变换；再通过特征匹配的方法，使用RANSAC方法，找到可视子集的目标附属位置；而后使用ICP方法，进行再次精准配准。

PCL代码：

// ... and downsampling the point cloud
  const float voxel_grid_size = 0.005f;
  pcl::VoxelGrid<pcl::PointXYZ> vox_grid;
  vox_grid.setInputCloud (cloud);
  vox_grid.setLeafSize (voxel_grid_size, voxel_grid_size, voxel_grid_size);
  //vox_grid.filter (*cloud); // Please see this http://www.pcl-developers.org/Possible-problem-in-new-VoxelGrid-implementation-from-PCL-1-5-0-td5490361.html
  pcl::PointCloud<pcl::PointXYZ>::Ptr tempCloud (new pcl::PointCloud<pcl::PointXYZ>); 
  vox_grid.filter (*tempCloud);
  cloud = tempCloud; 

  // Assign to the target FeatureCloud
  FeatureCloud target_cloud;
  target_cloud.setInputCloud (cloud);

  // Set the TemplateAlignment inputs
  TemplateAlignment template_align;
  for (size_t i = 0; i < object_templates.size (); ++i)
  {
    template_align.addTemplateCloud (object_templates[i]);
  }
  template_align.setTargetCloud (target_cloud);

  // Find the best template alignment
  TemplateAlignment::Result best_alignment;
  int best_index = template_align.findBestAlignment (best_alignment);
  const FeatureCloud &best_template = object_templates[best_index];

  // Print the alignment fitness score (values less than 0.00002 are good)
  printf ("Best fitness score: %f\n", best_alignment.fitness_score);

  // Print the rotation matrix and translation vector
  Eigen::Matrix3f rotation = best_alignment.final_transformation.block<3,3>(0, 0);
  Eigen::Vector3f translation = best_alignment.final_transformation.block<3,1>(0, 3);

后记：

        在去除外点，匹配已知的情况下，ICP的最小二乘问题总会得到一个最优解，即ICP的SVD方法总会有一个解析解。