AI:PR的数学表示-传统方法PR
前言:
接上一篇:AI:模式识别的数学表示
在图像处理PR领域,相对于ANN方法,其他的方法一般称为传统方法。在结构上,几乎所有的PR方法都是可解释的。且任一传统方法,在一定约束下,可以转换为SV近邻法,即与SVM方法具有相似性,且理论函数复杂度不小于同精度的基于SV的决策树方法。
而在规则和语义上,ANN方法一般是无法使用明确函数解释的,称之为PR的语义黑箱。
对于图像处理IP来说,一般形式下的模式函数都是(降维)压缩hash函数。
而对于传统模式识别方法,特征提取和模式识别模型一般都有固定的函数模型,甚至是纯粹的概率观测模型(如Bayes方法)。固定的函数模型的优势是语义可解析,缺点是缺失了极端泛用性。
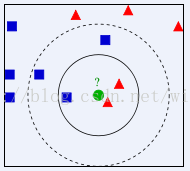
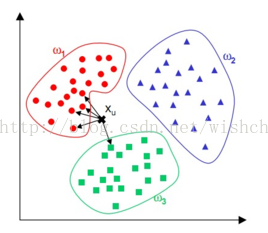
K近邻法:模式函数的近邻hash
从直观角度上看,相似的图片应该表示相似的语义,即相似的图片在集合张量空间内的距离较近,那么其模式值也应该是接近的,这就引出了模式函数的一般特性:近邻hash。
近邻hash定义:
对于函数 f( x ) = { X——>Y },其中f(x)是一个单射。Dx(t1,t2),Dy(t1,t2)表示距离函数。
且存在p>P(x){ P(x)> 0.9...9 }, 使得
Dx(x1,x2) <Dx(x1,x3) ——> Dy(y1,y2) <Dy(y1,y3) (蕴含式)
百科:KNN方法
欧式距离定义(2-范数)
因此,K近邻法从直观上描述了模式函数的自然语义-压缩近邻hash。
但近邻法的模式函数是这样的:
S(x)为取最小函数: S(xi) = min( Dx( xi, x ) ),运算符为“<”,实现方法为各种排序方法 Sort (yi){ yi ∈ Y} 。
语义分析:一般来说,近邻法模型是有语义的,而这个语义蕴含在距离判断函数Dx(
xi, x ) 里面,且另一个附加语义最近,表示了模式映射的一般特性,一旦你选择了什么样的距离,直接决定了会有什么样的分类结果。
贝叶斯方法:
贝叶斯方法是已知后验概率,收集条件概率,求取模型的先验分布的方法。
模型函数为贝叶斯公式和跃阶函数的复合函数。
参考文章:ML常用机器学习公式梳理
从思维方法上讲,贝叶斯方法表示了分类方法的一般极限,却是无语义的,纯粹从观测的角度分析结果。
PR的一般路径—线性可分判别函数
从样本出发直接设计分类器,而不去确定大概率情况下不会准确的条件概率和观测后验概率,是分类模型的形式转换要求。即样本分类一般有一个界面,这个界限对应了一个函数,即是分类器的模式函数。
从分界面的思想出发,设计分类函数,必然导致函数形式的具体化。直接在二维图像/张量空间里面寻找分类界面的函数形式,非常困难,因此模式识别发展为一般的传统模式识别方法:特征提取和模式识别。特征提取把图像从二维张量/欧氏空间,映射到N维向量空间,转化为特征集合;而模式识别只负责对特征集合进行分类,即把对N维向量特征再次进行压缩近邻hash,完成分类——模式函数建立。
传统IP模式识别的方法
定义X,和模式的种类Y,来确定函数
f( x ) = { X——>Y },其中f(x)是一个单射。
引入特征空间概念,分解为两个函数乘积/复合
定义X,和模式的种类Y,引入特征概念F 。模式 f( x ) = { X—>Y },分离处特征提取函数H(x),由此分解为特征函数 H(x)和 分类器/分类模型C(f)。
表示为f(
x ) = { X—>Y }=H(x)*C(f)或者C(
H(x) ) = {X—>F—>Y}。
意义:向量空间的压缩映射有完整的数学理论支持,且可以使整个PR系统围绕着模型逐步优化,且定能达到要求,符合工程学上复杂问题进行复杂度分解的一般要求。
文章:图像的局部特征综述-SIFT为例
——SIFT函数把图像块转化为128维向量空间中的向量
语义表示:特征函数
H(x)和 分类器/分类模型C(f)
必须都是近邻hash函数,且一般是压缩近邻hash函数。其中 特征函数
H(x)把二维欧氏空间中的图片集合压缩到一维欧式空间中的N维向量空间,而分类模型C(f)
完成模式函数 f(x) 的一般功能。
模式识别
经典SVM方法:SVM方法不直接对原始N维特征向量进行训练,寻找线性分类面,而是经过核函数映射,把N维向量映射到高维空间,寻找分类面,避开了非线性计算,分类时也使用了同样的过程。参考文章:支持向量机的近邻解释。

文章:支持向量机的近邻解释-(3)。 SVM完成特征高维映射,再进行判别分析。
经典ANN方法:ANN方法训练之后可视为分层复合连乘器,经过最后的判别层,把结果向量降低到0维,完成模式识别。
特征提取hash
特征提取的一些要求:缩放不变性、位移不变性、光照不变性等。也表示了相似的一般要求:一个物体在缩放、旋转、光线变化的环境中,所提取的特征也应该能表示此物体,即是特征也应该近邻。
基于不变性,出现了大量的局部特征,参考文章:图像的局部特征综述-SIFT为例。OpenCV几乎包含了已知的有效特征函数,包含在opencv\build\include\opencv2\features2d\features2d.hpp里面。即把2d图像转化为N维向量的函数。而全局特征函数比如HOG、LBP、HAAR等包含在检测特征里面。
意义:特征提取有什么意义?把2d图像转化为N维向量,是为了满足模型的要求。向量空间的压缩映射有完整的数学理论支持,且可以使整个PR系统围绕着模型逐步优化,且定能达到要求。
优势:专家得到的特征函数,从理论上给出了函数语义,怎么维持了不变性,在结构上怎样地保持近邻特性,甚至在语义上给出了可靠的支持,比如LBP表示的人脸模型方法。
压缩局限:每一个特征的产生,都是经过图像处理方面的专家经过理论证实且经过大量实验证明其在特定约束(比如旋转不变、位移不变性、光照不变性等的一个或多个)要求下有效的方法,是个经验过程。而对于不同类别的图像,可能特征近邻模式也不相同。以检测为例,人脸识别适合HARR和LBP,而行人检测更适合HOG,这表明了特定的图像集合即使在特征提取层面最优特征hash函数也会有不同,而特征模式的优化比模型本身更耗费精力,因为需要模型的反馈,而不是模型本身可以根据结果自行优化。

文章:图像的全局特征LBP。 图像的全局特征HOG。可以看出,两种不同全局特征的表示优势和适应范围。
HOG特征为例—(特征提取语义)
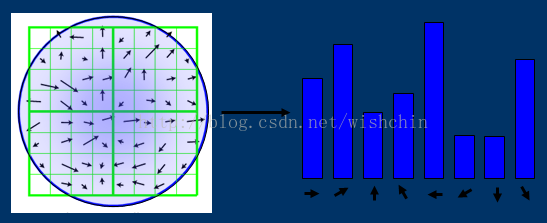
HOG特征使用局部梯度计算子(光照、旋转不变性),然后对每一个Cell块对梯度直方图进行投影(划分计算子),对每一个重叠块内的Cell进行对比度归一化(平移不变性),然后把所有Block内的向量组合成一个直方图(从二维欧式空间降低到一维欧式空间,使用块划分的模式)。
分别使用了归一化图像 N(X),梯度计算函数 G(p),直方图投影 P(g),归一化直方图 N(p),把二维降低到一维的函数 C(h),复合函数为N()*G()*P()*N()*C(),也可以表示为C( N( P( G( N(X) ) ) ) ) 。
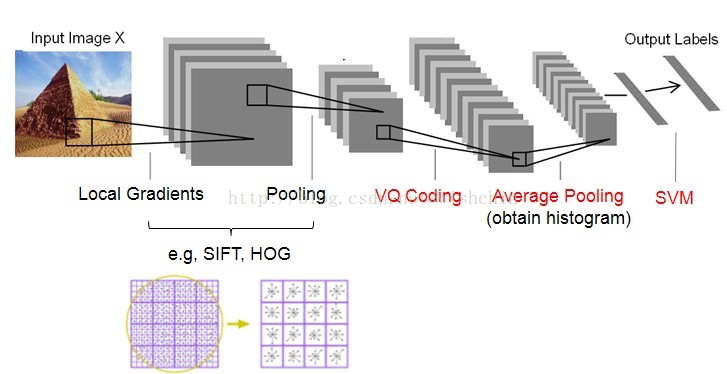
而对于整幅图像,以场景识别的特征SIFT+VQ方法为例,如下图。
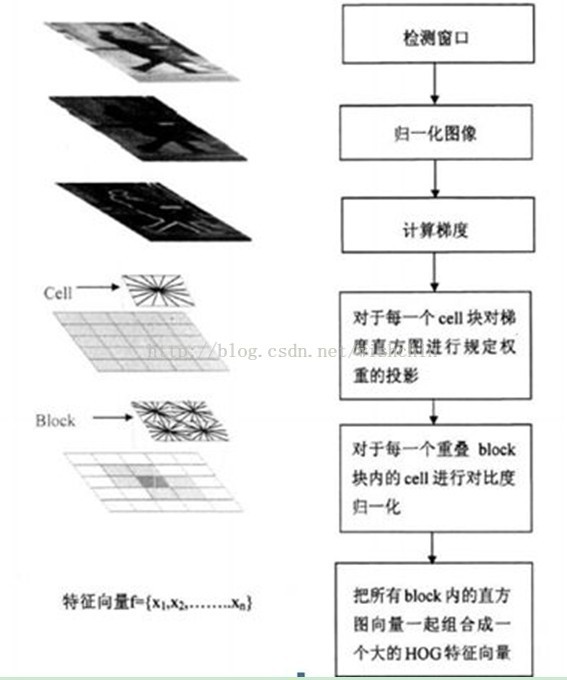
SIFT特征提取+VQ编码,图片来自:在线场景感知ScSPM和LLC总结
优势和缺点:优势是特征提取特定的方法给出了明确的语义,
缺点是形式上的固定限制了特征提取的可表达性,即即便如广受好评的SIFT特征和HOG特征,特征提取压缩函数形式上的固定决定了其压缩损失的固定性,这种损失率不会随着数据的增多而降低。
SIFT特征局限:即使广泛使用的SIFT特征,特征hash准确性和泛化性能出类拔萃,但在ImageNet ILSVRC比赛的最好结果的错误率也有26%以上,而且常年难以产生突破。这也验证了一个算法的普遍难题:没有一个合适的算法适合所有问题,如果在一个问题上体现足够的准确,那么在一个问题上也能体现足够的错误。而最通用的算法,则代表着通用的普通性能。
CNN方法—一站式PR方法(特征提取方向)
随着超量类别PR和高精度的需求,人工特征方法局限性凸显出来,特征hash压缩映射因其压缩损失,在海量的同类数据集上表现的近邻特性变差,而在不同类别的数据上面隔离性又出现问题。
既然人工构建的特征hash函数并不能满足每一个场景的需求,每个经验都有局限,且特征提取的压缩映射必然导致压缩损失,为何不略过此环节,使用数据来完成此过程。越多的数据可生成越精确的分类结果,这就引出了图像特征提取的自动化方法、一站式图像处理PR方法——CNN方法。IPPR又从分治法回到一站式方法。
从2012年AlexNet横空出世,获取制高点之后,图像处理PR进入了CNN方法的汪洋大海,而后以横扫之势统治了整个IPPR界。
后来随着类别的增加,和准确度要求的提高,CNN走向了更大、更深,且在这条路上越走越远。且随着对网络结构的进一步分析,特定的网络结构可以进行语义分析,甩开了“语义黑箱”的帽子。
Baging方法:传统方法随机森林应对多类和高精度挑战
在 Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? 这篇论文里,分析了各个家族的分类器结构、效果、以及分类器极限。这样介绍:we evaluate 179 classifiers arising from17families (discriminant analysis, Bayesian, neural networks,support vector machines, decision trees, rule-based classifiers,boosting, bagging, stacking, random forests and other ensembles,generalized linear models, nearest-neighbors, partial leastsquares and principal component regression, logistic andmultinomial regression, multiple adaptive regression splines andother methods), implemented in Weka, R (with and without thecaret package), C and Matlab, including all the relevantclassifiers available today. We use121 data sets。使用了121个经典数据集,分析了17个族的179种分类器,得出了随机森林方法乃是综合评价最好的集成学习方法。甚至:The classifiers mostlikely to be the bests are the random forest (RF) versions,the best of which (implemented in R and accessed via caret)achieves 94.1% of the maximum accuracy overcoming 90% in the84.3% of the data sets. However, the difference is notstatistically significant with the second best。除了随机森林方法,第二好的方法无法评判。
随机森林的优势一:精度优势。决策树对特征的权重进行选择,置为不同权重(即指明了那些特征的重要性),理论上数据越多且弱分类器相应增加的情况下,随机性带来的特征提取损失会相应降低,因为对特征进行赋权的方法,使组合分类器已经明显包含了特征选择的功能,可逐步降低特征hash的损失。直觉上,随机森林在精度上必然超过其他机器学习方法,且数据越多优势越明显。
随机森林的优势二:多类优势——随机森林进行多分类和模型调优。随机森林的多类优势是由决策树本身的结构而定,并且弱分类器组合的投票模型,有效的降低多类的识别误差。
随机深林的极限:随机深林使用随机策略保证最大似然概率为无偏估计,其复杂度大于基于SV的单颗决策树方法,甚至在一些时刻复杂度超过使用多项式核的SVM方法。
模型的处理极限
根据模型的PAC可学习理论分析,每一种分类器都有其处理极限,参考:PAC学习理论-机器学习那些事。
PAC可学习理论的公式:下列公式是机器学习的泛化误差和一些学习器参数的关系
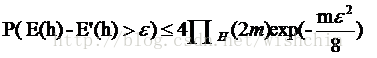
在机器学习中,简单的算法意味着增长函数
更广泛的场景意味着样本的分布更加复杂,因此分类界面也更加复杂,以分界面思想构建模式分类器的思路表明,代表分类界面的模型函数复杂度会随之增加。而特定类型的传统PR方法模式函数的形式是固定的,在理论上产生了特定的“局限性” 的,分类准确度可以使用PAC学习理论的方法计算出来。特定函数形式的模式识别准确度、泛化误差都受到模型本身VC维的限制。
更加复杂的分类面要求更复杂的分类函数,PAC理论给出了近似分类面的模式函数复杂度代价,更高的精度意味着更接近真实的分类面,固定领域模式函数的复杂度和泛化能力可以通过PAC计算得出。
既然ANN没有固定的函数形式,特定复杂的ANN可以有不受限制的VC维,理论上可以突破传统模式识别方法的可学习性限制。ANN理论上成为突破高精度和多类识别挑战的唯一选择。