NLP学习笔记-朴素贝叶斯
朴素贝叶斯(Native Bayes)算法是根据概率理论贝叶斯定理的分类算法，通过计算样本属于不同类别的概率来分类。朴素贝叶斯是贝叶斯分类器里的一种方法，朴素贝叶斯分类器可以说是最经典的基于统计的机器学习模型。
贝叶斯定理
回归到概率中学过的贝叶斯定理
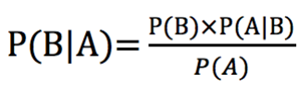
在分类算法的应用中，可以将其转化为下面的式子
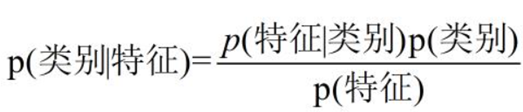
把公式中的A看作样本的特征，B看作分类目标的类别，那么就可以把公式分解为以下的部分。
P（A）称为先验概率，即在B之前，什么都不知识时对A事件概率的判断。
P(A|B)称为后验概率，即在B之后，对A事件概率的重新评估。
P(B|A)/P(B)称为可能性函数，这是一个调整因子，使得预估概率更接近真实概率。
所以条件概率可以理解为：后验概率=先验概率×调整因子
如果可能性函数大于1，证明先验概率被增强，A发生的可能性变大；
如果可能性函数等于1，证明B事件无助于判断事件A的可能性；
如果可能性函数小于1，证明先验概率被削弱，A发生的可能性变小。
基于贝叶斯决策理论的分类方法
那么是通过什么方式来进行分类的呢，假设有两类数据组成的数据集如下面这张图。
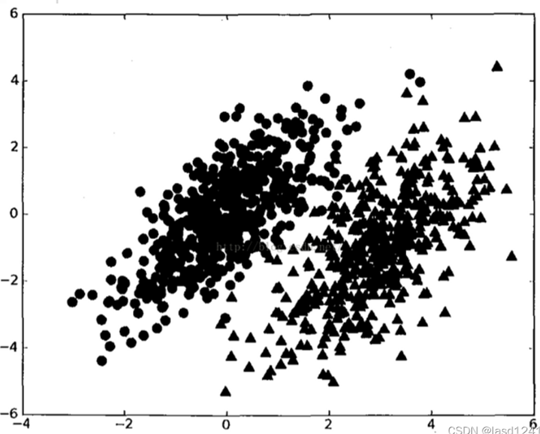
如果已经知道了以上两个概率分布的参数，假设P1（x,y）为点（x,y）属于第一个类别的概率；P2（x,y）为数据点属于类别二分概率。
贝叶斯决策理论的核心就是选择高概率所对应的类别，选择概率最高的决策。如果P1大于P2，那么（x,y）就会被判别属于第一个类别。即在上面的式子P（类别|特征）中，在特征不变的情况下选择使P更大的类别，那这个类别就是该特征所属的类别。
举例
下面我们借用参考的例子，来更加清晰具体的了解。
捕捞到了一批鱼其中有黑鱼和三文鱼两类，我们虽然无法方便这两种鱼但我们可以测量他肚皮亮度的等级（比如最白为10级，最黑为1级）。这时我们得到了一批标注好类别的黑鱼和三文鱼，那么借助这些我们就可以通过使用朴素贝叶斯的类器来给捕到的鱼打上标签，将三文鱼和黑鱼分类出来。
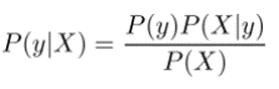
再回到贝叶斯公式，那么在这个例子里每条鱼肚皮的亮度就是特征X，黑鱼和三文鱼就是要分类的目标c0和c1。那么假如我们测得了某条鱼肚皮的亮度为2，我们要比较的P（y=c0|X=2）和P（y=c1|X=2），也就是上面说的选择概率最高的决策。那么公式右边的部分都可以通过样本得到，就可以算出左边的值进行比较了。
实际使用中，贝叶斯算法也常用于垃圾邮件的检验。假设有一份邮件，包含：代开，增值税，发票，sep。要通过这几个词，预测其为垃圾邮件的概率，即转化为求P（垃圾|代开,增值税,发票,sep），那么使用贝叶斯公式和全概率公式，就可以转换成下面的式子。
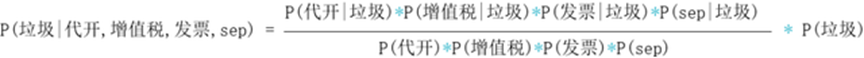
通过对样本中各个词语为垃圾邮件的计算，就可判断出这份邮件是否为垃圾。
零概率问题
认真思考上面关于垃圾邮件的算式你会发现，当模型训练过程中没有某个记录的特征，或某个分类中没有记录的特征，即在上式中可能出现P（y|X）为0分情况，那么在乘积过程中，整个分子都为0，算式的结果也为0。这样就无法真实表示某个特征在类别中的概率。
拉普拉斯平滑
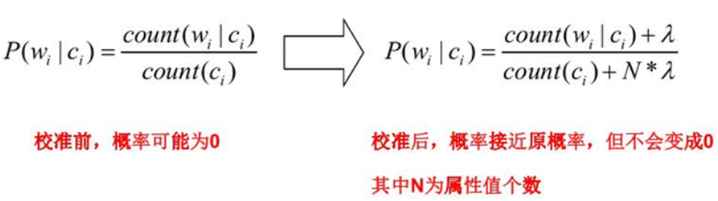
浮点数溢出问题
然而还会遇到另外一个问题，就是下溢出，就是各标签概率的值过小，在乘积的过程中，会导致浮点数的溢出，比如在计算乘积
大部分因子都很小时，乘积为一个非常小的数次，会导致计算出错。一种解决的办法就是对乘积取自然对数，在代数中 l n ( a ∗ b ) = l n ( a ) + l n ( b ) ，于是通过求对数可以避免下溢出或者浮点数舍入导致的错误，如下图把概率的相乘转化为相加。同时，采用自然对数进行处理不会有任何损失。
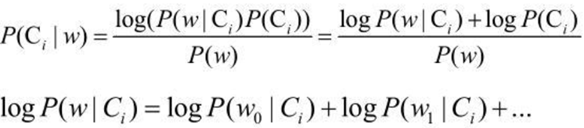
朴素Naive
一直在讲朴素贝叶斯（Naïve Bayes），贝叶斯即依据贝叶斯定理，那么何为朴素呢？其实就是代表简化问题的复杂度，朴素的意思就是“特征独立性假设”。独立性假设一般指“条件独立性假设”，但在处理序列问题时还有“位置独立性假设”。
条件独立性假设
假设识别一个人的性别需要身高和体重两个特征，我们这道身高和体重往往存在关联，但在贝叶斯分类器中，这两个特征没有关联，所以身高180cm体重50kg，则P（x1=180cm，x2=50kg）=P（x1=180cm）*P（x2=50kg）。
身高一米八体重五十的概率，等于两特征概率的乘积，虽然我们知道180cm概率很大，50kg概率也很大，但同时具备以上两特征的概率比较小，然而在贝叶斯独立性假设中，他们相对独立，所以算出的概率肯定大于实际值。这就是条件独立性假设。
位置独立性假设
使用朴素贝叶斯解决序列分类问题时，对于不考虑序列中的各特征向量的位置。假如在文本挖掘中，“我|喜欢|猫”这个句子中有三个特征向量，分别为向量“我”、向量“喜欢”、向量“猫”。
然而通过朴素贝叶斯计算分子时并不会考虑到特征向量的位置，因此在朴素贝叶斯看来“我|喜欢|猫”和“猫|喜欢|我”是同一个分类任务，这就是位置的独立性。
朴素贝叶斯基于概率理论进行分类，原理和实现都比较简单，学习和预测效率也很高，虽然其朴素性显得不切实际，但是在处理垃圾邮件过滤等任务时效果很好，是一种经典的分类算法。
参考文献：
https://baijiahao.baidu.com/s?id=1699439532250738747&wfr=spider&for=pc
https://blog.csdn.net/lasd12415/article/details/122203555
https://blog.csdn.net/li8zi8fa/article/details/76176597
https://mp.weixin.qq.com/s/_oTPcevGiaXl-bKa9nHD_w
