NLP学习笔记-感知机

　　感知机是一个二类分类的线性分类模型。输入为实例的向量，输出为类别，取值为+1或-1。实际上是将实例通过一个超平面划分为正负两类，属于判别模型。感知机学习旨在求出将训练 数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度 下降法对损失函数进行极小化，求得感知机模型．感知机学习算法具有简单而易 于实现的优点，分为原始形式和对偶形式．

 

感知机模型

　　输入空间x为特征向量，输出空间y为1或-1，即对x的分类，由输入到输出的函数为f(x)=sign(w·x+b)，称为感知机。b叫做偏置常数，w·x表示w和x的内积，sign是符号函数。

　　　　

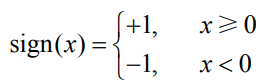
　　线性方程w·x+b=0对应在空间中的一个超平面S，w是超平面法向量，b是截距，这个面将特征划为两部分。感知机学习就是通过训练集，求得感知机模型中的参数w，b。然后用通过学习的感知机模型，对于新的输入给出输出。

 

感知机学习策略

　　 

　　对于一个数据集T，如果存在一个超平面wx+b=0可以将正负实例点完全正确划分，那么数据集T为线性可分数据集。

　　感知机的学习正是寻找这样的平面，为了能找到，需要定义损失函数并使损失函数最小。

　　 

　　损失函数是对于数据集中的误分类点，使用上式计算该点到超平面S的距离,求其总和就得到了感知机学习的损失函数。定义为

 　　 

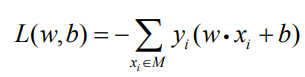
  　　其中M为误分类点的集合。误分类点越少，误分类点离超平面越近，损失函数就越小。

 

感知机的学习算法

　　感知机的学习算法就是求解损失函数式最优化的问题

　　原始形式

　　　　输入训练集T和学习率n；

　　　　输出为w，b；感知机模型为f(x)=sign(w·x+b)

　　　　（1）选取初值w0，b0，一般默认为0。

　　　　（2）在训练集中选取数据x，y

　　　　（3）如果y（w·x+b）≤0，即不符合要求，那么

　　　　　　　　w=w+nyx    b=b+ny

　　　　（4）转到（2），直到没有误分类点

 

　　对偶形式 

　　　　由原始形式可知，每次错误时w增加nyx，b增加ny，实际上w和b可以写为

　　　　

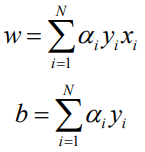
　　　　若经过m次修改，则a=mn。对偶学习的步骤可以写为

　　　　输入训练集T和学习率n；

　　　　输出为w，b；感知机模型为

　　　　（1）a，b赋值为零

　　　　（2）在训练集中选数据（x,y）

　　　　（3）如果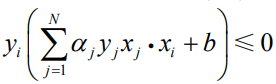

　　　　　　　　a=a+n  b=b+ny

　　　　（4）转至（2）直至没有误分类数据