[数据结构]哈夫曼编码实现文本压缩
要求:输入字符串,输出字符串的哈夫曼编码
输入:一行字符串。
输出:n行,n为包含的不同字符数
每行输出该字符的出现次数和编码。
最后一行输出该字符串转换成哈夫曼编码的形式。
实验结果:
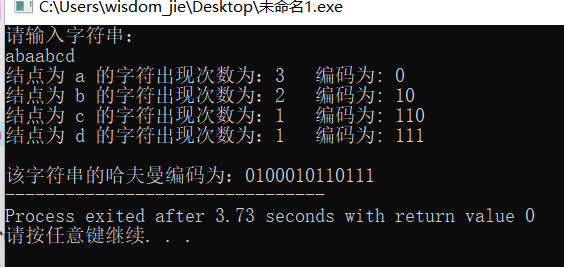
/*补充知识:哈夫曼树
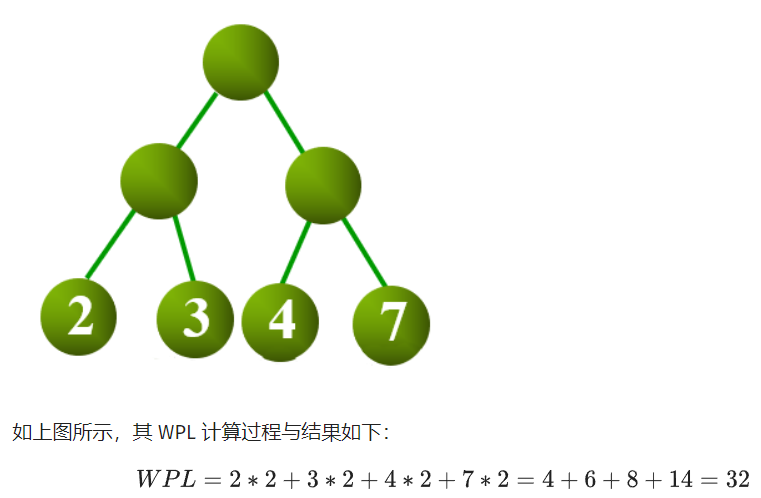
树的带权路径长度
设二叉树具有n个带权叶结点,从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度(Weighted Path Length of Tree,WPL)。
设wi为二叉树地l个叶结点的权值,li为从根结点到第i个叶结点的路径长度,则 WPL 计算公式如下:
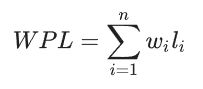
结构
对于给定一组具有确定权值的叶结点,可以构造出不同的二叉树,其中,WPL 最小的二叉树 称为 霍夫曼树(Huffman Tree)。
对于霍夫曼树来说,其叶结点权值越小,离根越远,叶结点权值越大,离根越近。
霍夫曼算法
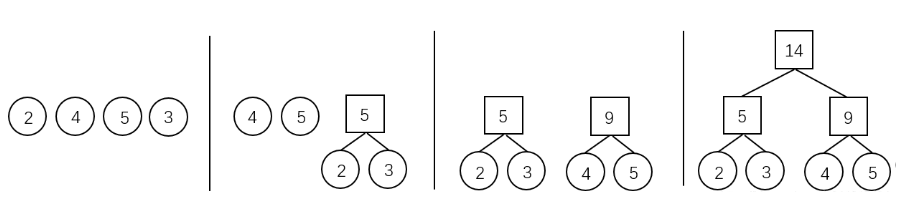
霍夫曼算法用于构造一棵霍夫曼树,算法步骤如下:
- 初始化:由给定的n个权值构造n棵只有一个根节点的二叉树,得到一个二叉树集合F。
- 选取与合并:从二叉树集合F中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树,这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
- 删除与加入:从F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到F中。
- 重复 2、3 步,当集合中只剩下一棵二叉树时,这棵二叉树就是霍夫曼树。
霍夫曼编码
霍夫曼树可用于构造 最短的前缀编码,即 霍夫曼编码(Huffman Code),其构造步骤如下:

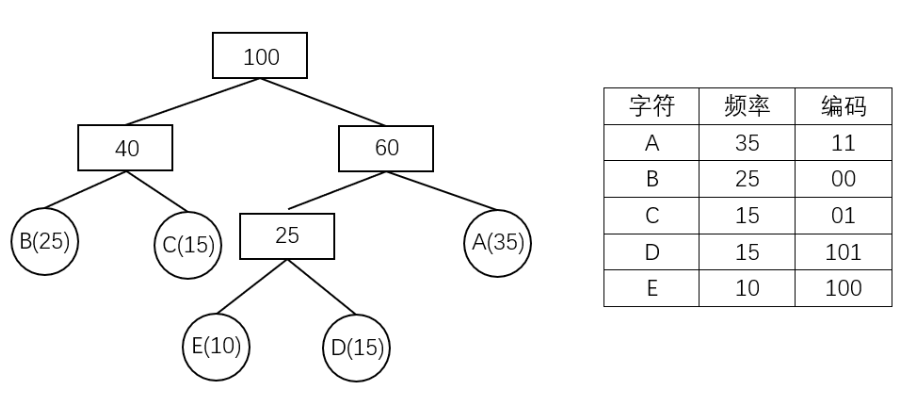
*/
OK,进入正题,我们来看看如何通过上面的步骤来将字符串转化为哈夫曼编码。
实验步骤:

将字符串读进s数组后,进入calcu函数。在calcu函数中,我们将输入的字符串中每个字符映射到以其ASCII码为下标的数组arr中,用arr数组记录每个字符出现的次数,比如arr[x]=3说明ASCII为x的字符出现了3次,我们就知道了每个字符所占的权重,方便接下来的createHuffmanTree()中哈夫曼以结点权重建树。
第二个for循环统计有多少字符出现过,就知道了哈夫曼树中有多少叶子结点。

建树中,记录每个结点的权重weight叶子结点即为字符出现次数,非叶子结点为以其为根的子树上叶子结点权重之和。value结点记录叶子结点实际代表的字符。
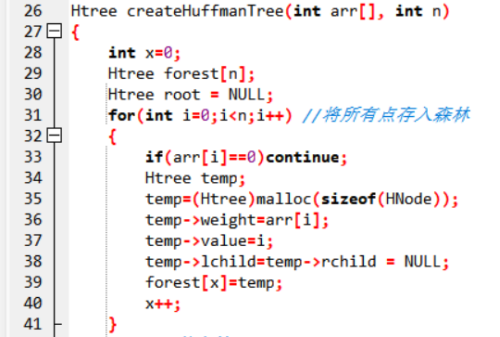
在建树时,首先通过arr数组将其中所有出现过的字符,构建一个单独的结点,并且全部归纳在数组forest数组中,这样forest数组就存储了一个全部结点的森林,接下来我们来对结点进行合并,最终构建一棵哈夫曼树。
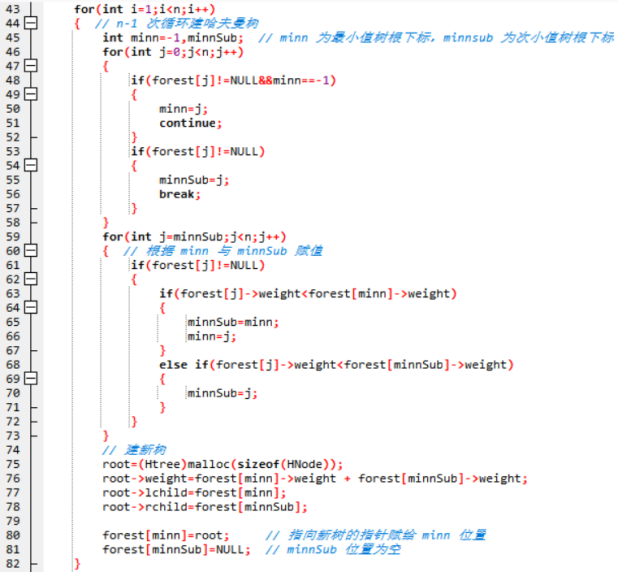
接下来通过n-1次循环,每次合并两个结点。通过两个for循环在forest森林中找到权值最小的结点minn和次小的结点minnsub,然后将他们合并在一个空的根节点上,形成一棵子树,并放入forest森林中,同时删除在森林中删除这两个结点。子树的根节点记录该树的权值,即两结点权值之和。然后继续在森林中继续找权值最小的两子树合并。当只剩下一棵二叉树时,这棵二叉树就是霍夫曼树。

接下来就可以通过刚才建好的哈夫曼树计算哈夫曼编码了。如果只有一种字符,那么直接输出。否则对该树进行深度优先遍历,如果是向左子树遍历,向编码中加入一个0,如果是向右遍历在编码中加入1。当找到叶子结点是,说明找到了字符输出它出现的次数weight和编码,同时将该字符的编码方式记录到diction字典中,方便接下来对照将字符串中每个字符转成编码。
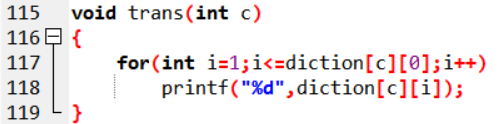

遍历字符串将每个字符送入trans函数将其转化为编码输出。
于是,大功告成,字符串被转换成了哈夫曼编码!!!
#include<stdio.h> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char s[1000005]; int arr[150],N,diction[200][200];//ASCII有128位 typedef struct HNode { int weight; char value; HNode *lchild, *rchild; } * Htree; void calcu(int l) { for(int i=0;i<l;i++) { char x=s[i]; arr[x]++; } for(int i=1;i<=128;i++) if(arr[i]!=0)N++; } Htree createHuffmanTree(int arr[], int n) { int x=0; Htree forest[n]; Htree root = NULL; for(int i=0;i<n;i++) //将所有点存入森林 { if(arr[i]==0)continue; Htree temp; temp=(Htree)malloc(sizeof(HNode)); temp->weight=arr[i]; temp->value=i; temp->lchild=temp->rchild = NULL; forest[x]=temp; x++; } n=x;//n种字符 for(int i=1;i<n;i++) { // n-1 次循环建哈夫曼树 int minn=-1,minnSub; // minn 为最小值树根下标,minnsub 为次小值树根下标 for(int j=0;j<n;j++) { if(forest[j]!=NULL&&minn==-1) { minn=j; continue; } if(forest[j]!=NULL) { minnSub=j; break; } } for(int j=minnSub;j<n;j++) { // 根据 minn 与 minnSub 赋值 if(forest[j]!=NULL) { if(forest[j]->weight<forest[minn]->weight) { minnSub=minn; minn=j; } else if(forest[j]->weight<forest[minnSub]->weight) { minnSub=j; } } } // 建新树 root=(Htree)malloc(sizeof(HNode)); root->weight=forest[minn]->weight + forest[minnSub]->weight; root->lchild=forest[minn]; root->rchild=forest[minnSub]; forest[minn]=root; // 指向新树的指针赋给 minn 位置 forest[minnSub]=NULL; // minnSub 位置为空 } return root; } void huffmanCoding(Htree root,int x,int arr[]) // 计算霍夫曼编码 { if(N==1) { printf("结点为 %c 的字符出现次数为:%-4d 编码为: 1",s[0],arr[s[0]]); return ; } if(root!=NULL) { if(root->lchild==NULL&&root->rchild==NULL) { printf("结点为 %c 的字符出现次数为:%-3d 编码为: ",root->value, root->weight); for (int i=0;i<x;i++) { diction[root->value][i+1]=arr[i]; printf("%d",arr[i]); } diction[root->value][0]=x; printf("\n"); } else { arr[x]=0; huffmanCoding(root->lchild,x+1,arr); arr[x]=1; huffmanCoding(root->rchild,x+1,arr); } } } void trans(int c) { for(int i=1;i<=diction[c][0];i++) printf("%d",diction[c][i]); } int main() { XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXX 开动脑筋哦 XXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX }





