经典排序算法【转】

动画图解 :http://student.zjzk.cn/course_ware/data_structure/web/flashhtml/maopaopaixu.htm (更改后缀拼音)

/*
    冒泡排序算法的运作如下：

    1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。
    2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
    3.针对所有的元素重复以上的步骤，除了最后一个。
    4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
*/
public void BubbleSort<T>(T[] needSort) where T : IComparable
        {
            T temp;
            for (int i = 0; i < needSort.Length - 1; i++)
            {
                for (int j = i + 1; j < needSort.Length; j++)
                {
                    if (needSort[i].CompareTo(needSort[j]) > 0)
                    {
                        temp = needSort[i];
                        needSort[i] = needSort[j];
                        needSort[j] = temp;
                    }
                }
            }
        }

冒泡排序 BubbleSort

快速排序采用一种“分而治之、各个击破”的观念。
/*
    快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

    步骤为：

    1.从数列中挑出一个元素，称为 "基准"（pivot），
    2.重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）    。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
    3.递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
    递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。
    举个例子

    如无序数组[6 2 4 1 5 9]

    a),先把第一项[6]取出来,

    用[6]依次与其余项进行比较,

    如果比[6]小就放[6]前边,2 4 1 5都比[6]小,所以全部放到[6]前边

    如果比[6]大就放[6]后边,9比[6]大,放到[6]后边,//6出列后大喝一声,比我小的站前边,比我大的站后边,行动吧!霸气十足~

    一趟排完后变成下边这样:

    排序前 6 2 4 1 5 9

    排序后 5 2 4 1 6 9



    b),对前半拉[5 2 4 1]继续进行快速排序

    重复步骤a)后变成下边这样:

    排序前 5 2 4 1

    排序后 1 2 4 5

    前半拉排序完成,总的排序也完成:

    排序前:[6 2 4 1 5 9]

    排序后:[1 2 4 5 6 9]

    排序结束

    以下代码实现仅供参考
*/

public class Code
    {
        public void QuickSort<T>(T[] needSort, int low, int high) where T : IComparable
        {
            int targetPosition = 0;

            if (low < high)
            {
                targetPosition = PositionArrange(needSort, low, high);
                QuickSort(needSort, low, targetPosition - 1);
                QuickSort(needSort, targetPosition + 1, high);
            }
        }

        public int PositionArrange<T>(T[] needSort, int low, int high) where T : IComparable
        {
            T tempData = needSort[low];
            while (low < high)
            {
                while (low < high && needSort[high].CompareTo(tempData) > 0)
                {
                    high--;
                }

                needSort[low] = needSort[high];

                while (low < high && needSort[low].CompareTo(tempData) <= 0)
                {
                    low++;
                }

                needSort[high] = needSort[low];
            }

            needSort[low] = tempData;
            return low;
        }
    }

快速排序 quickSort

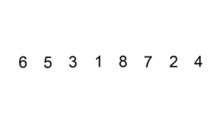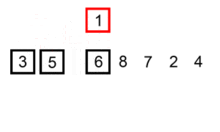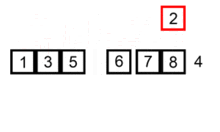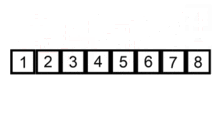
使用插入排序为一列数字进行排序的过程
/*
一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5
如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找排序。
*/

public void InsertSort<T>(T[] needSort) where T : IComparable
        {
            for (int i = 1; i < needSort.Length; i++)
            {
                T tempData = needSort[i];
                int j = i;
                while (j > 0 && needSort[j - 1].CompareTo(tempData) > 0)
                {
                    needSort[j] = needSort[j - 1];
                    j--;
                }

                needSort[j] = tempData;

                //for (int j = 0; j < i; j++)
                //{
                //    if (needSort[i].CompareTo(needSort[j]) < 0)
                //    {
                //        T tempData = needSort[i];
                //        needSort[i] = needSort[j];
                //        needSort[j] = tempData;
                //    }
                //}
            }
        }

插入排序 insertSort

/*
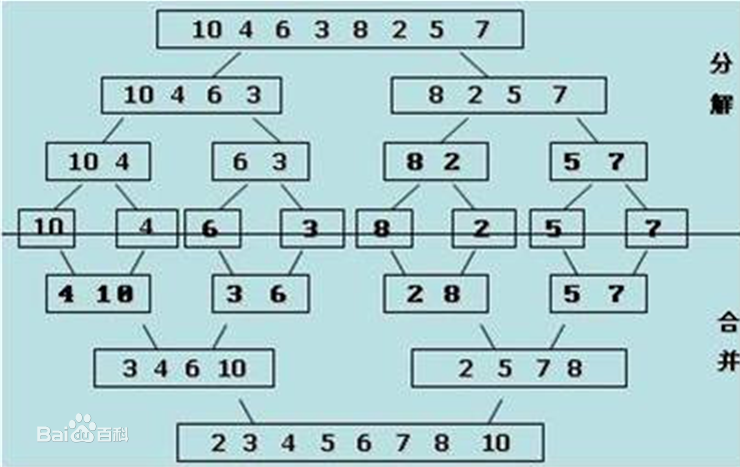
    算法描述
    归并操作的过程如下：

    申请空间，使其大小为两个已经排序串行之和，该空间用来存放合并后的串行
    设定两个指针，最初位置分别为两个已经排序串行的起始位置
    比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
    重复步骤3直到某一指针到达串行尾
    将另一串行剩下的所有元素直接复制到合并串行尾
*/
public class CodeSample
    {
        public void DataMerge<T>(T[] needSort, int low, int middle, int high, T[] temp) where T : IComparable
        {
            Console.WriteLine("low:{0} middle:{1} high:{2}", low, middle, high);
            foreach (T t in needSort)
            {
                Console.Write(t + " ");
            }

            Console.WriteLine();
            Console.WriteLine("---------------");
            int i = low, j = middle;
            int k = 0;
            while (i < middle && j < high)
            {
                if (needSort[i].CompareTo(needSort[j]) < 0)
                {
                    temp[k++] = needSort[i++];
                }
                else
                {
                    temp[k++] = needSort[j++];
                }
            }

            while (i < middle)
            {
                temp[k++] = needSort[i++];
            }

            while (j < high)
            {
                temp[k++] = needSort[j++];
            }

            for (int v = 0; v < k; v++)
            {
                needSort[low + v] = temp[v];
            }
        }

        public void MergeSort<T>(T[] needSort, int low, int high, T[] temp) where T : IComparable
        {
            if (low + 1 < high)
            {
                int middle = (low + high) / 2;
                MergeSort(needSort, low, middle, temp);
                MergeSort(needSort, middle, high, temp);
                DataMerge(needSort, low, middle, high, temp);
            }
        }
    }

/*
    测试数据:int[] needSort = { 11, 5, 26, 9, 11, 8, 3, 2, 1 };
    输出
        low:0 middle:1 high:2
        11 5 26 9 11 8 3 2 1
        ---------------
        low:2 middle:3 high:4
        5 11 26 9 11 8 3 2 1
        ---------------
        low:0 middle:2 high:4
        5 11 9 26 11 8 3 2 1
        ---------------
        low:4 middle:5 high:6
        5 9 11 26 11 8 3 2 1
        ---------------
        low:7 middle:8 high:9
        5 9 11 26 8 11 3 2 1
        ---------------
        low:6 middle:7 high:9
        5 9 11 26 8 11 3 1 2
        ---------------
        low:4 middle:6 high:9
        5 9 11 26 8 11 1 2 3
        ---------------
        low:0 middle:4 high:9
        5 9 11 26 1 2 3 8 11
        ---------------
        1 2 3 5 8 9 11 11 26
        请按任意键继续. . .
*/