「CF506E」Mr. Kitayuta's Gift 题解
题目简介
给一个小写字符串 \(s\) ,往 \(s\) 里面插 \(n\) 个数字得到 \(t\) 。要求 \(t\) 为回文串,求方案数。
分析
\(\color{black}{\mbox{O}}\)\(\color{red}{\mbox{rzqm}}\)说,这道题就是一个区间DP转有限状态自动机再优化建图后进行矩阵加速。

没有问题……
\(\color{red}\P\) step 1. 区间DP
定义 \(N=|s|+n\) ,即 \(t\) 的长度。
鉴于回文串的特殊形式,考虑从外往里添加字符。每添加一个字符,对 \(s\) 能匹配则进行匹配。
定义一下 \(DP\) 状态:\(f[i][l][r]\) 表示当前 \(t\) 已经确定了前 \(i\) 个和后 \(i\) 个字符,\(s[l],s[l+1],\dots,s[r]\) 还未被匹配的方式。
为了简便,现在只考虑 \(|s|\in\{x|x=2k,k\in\Z\}\) 的情况。
分类讨论:
s[l]==s[r]&&l+1==r:只能填一种字符来匹配 \(s[l]\) 和 \(s[r]\),所以\(f[i][l][r]=f[i-1][l][r]\times 25\)s[l]==s[r]&&l+1!=r:匹配 \(f[i][l-1][r-1]=f[i-1][l][r]\),不匹配 \(f[i][l][r]=f[i-1][l][r]\times 25\)s[l]!=s[r]:匹配其中一个 \(f[i][l+1][r]=f[i][l][r-1]=f[i-1][l][r]\),一个都不匹配 \(f[i][l][r]=f[i-1][l][r]\times 24\)
\(\color{red}\P\) step 2. 转有限状态自动机
名字听起来高大上,其实也不复杂。我们将 \(F[i]=F[i-1]\times 24\) 的状态称为红点,将 \(F[i]=F[i-1]\times 25\) 的状态称为绿点。例如,当 \(s=\)abaac时,根据 \(s\) 的匹配状态,就可以画出这样一幅图:
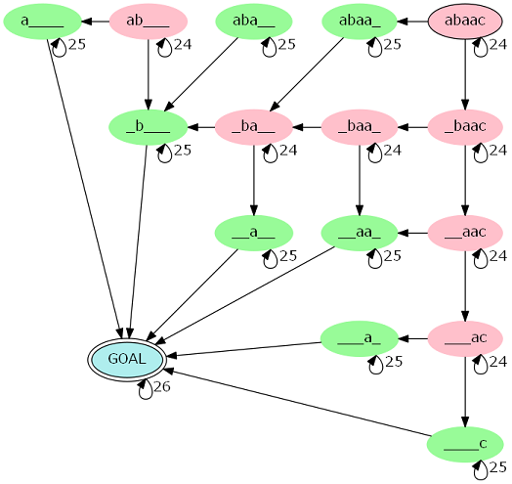
\(\color{red}\P\) step 3. 优化建图
考虑刚才的 \(DP\) 式,本来已经可以使用矩阵优化,但是 \(n\) 的范围很大(\(\le 10^9\)),且节点数很多(\(|s|^2\)),所以肯定会超时。
现在想一想怎么优化。
将自动机上面的图剖分成一条一条的链,对于两条红点数量相同的链,它们对答案的贡献与红点的具体位置无关,因此本质上是一样的,这意味着本质不同的链只有 \(s\) 条(红点数量只能取 \(0\)~\(s-1\) )。
我们将每条链转为这种形式:

将红点全部连起来,再连向绿点,把每个红点都看作一个起点,我们可以得到这样一张图:
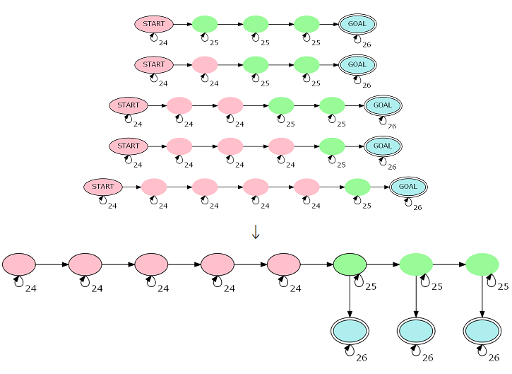
此时的点数基本可以稳定为 \(|s|\) 。
\(\color{red}\P\) step 4. 矩阵加速
没什么可讲的了……
再卡卡常?……
\(\color{red}\P\) other. 长度为奇
其实也没什么太多的,只需要将那些与终点相连的绿色点为偶数的链情况减去就可以。因为如果它匹配到最后剩两个相同字符,那么肯定 \(|t|\) 不为奇(感性理解)
\(AC\ Code\)
//蒟蒻的代码太冗乱了,不好意思放出来
参考的 \(\texttt{blog}\):
Codeforces Round #286 Editorial (Complete) - Codeforces
题解 CF506E 【Mr. Kitayuta's Gift】 - shadowice1984 的博客 - 洛谷博客 (luogu.com.cn)
【CF506E】Mr. Kitayuta's Gift dp转有限状态自动机+矩阵乘法 - CQzhangyu - 博客园 (cnblogs.com)
题解 CF506E 【Mr. Kitayuta's Gift】 - xht37 的洛谷博客 - 洛谷博客 (luogu.com.cn)
还有 \(\color{black}{\mbox{O}}\)\(\color{red}{\mbox{rzqm}}\) 的帮助(QwQ)


