简单堆结构详解

　　堆的本质就是一棵完全二叉树。

　　简单的堆可以分为两种：大顶堆与小顶堆。

0.为什么选择堆

---

　　在OI中，我们经常遇到一类问题，需要重复寻找最大值或最小值，如果我们每次都遍历一遍数组或每次都 sort 一遍，时间复杂度会非常之高，有可能出现 O（n²）的悲剧。这时候，亲爱的堆就出现了。

　　堆只需要通过更改部分关系，来维护整个堆结构。

　　堆有一个优秀的时间复杂度——O（n log n）

　　老师们常说，带log的都很厉害……

1.大顶堆与小顶堆的定义

---

　　顾名思义，当我们在构建二叉堆时，如果最大值在root( 树根，tree[1] ) 上，并且堆内父亲的值都大于等于儿子的值，就是大顶堆（顶部值最大）；

　　如果最小值在root上，并且堆内父亲的值都小于等于儿子的值，就是小顶堆（顶部值最小）。

2.堆的基本操作

---

　　堆有两个基本操作——put(data)存入值，get()获得堆的顶部值(root)。

2.1建立大顶堆

while(n--){
    scanf("%d",&data);
    put(data);
}

　　put函数需要实现：

1. 在堆尾增加一个值data；
2. 维护堆的关系

　　如何维护堆的结构：

1. 从堆尾data处，沿着二叉树一级一级向上找，不断更新父子关系，直到堆关系正确。

void put(int data){
    int ch,fa;//child,father
    heap[++heap_size]=data;//heap_size为全局变量 堆内元素个数
    ch = heap_size;//从堆尾开始查找 
    while(ch>1){//child不为根 
        fa = ch / 2;//父亲位置 
        if(heap[ch] <= heap[fa])break;//如果child不够大，就没必要冒上去
        swap(heap[ch],heap[fa]);//否则交换二值 
        ch = fa;//更新 
    }
}

　　如此而来就能保证，堆中的父亲一定比儿子大了。

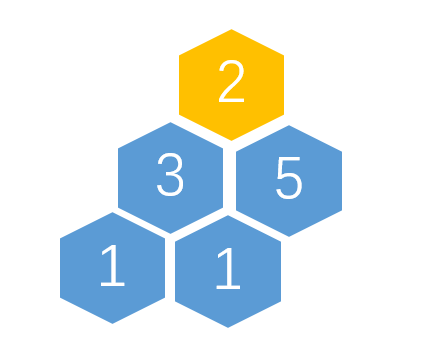
　　如果你不能理解，那么请看图：

　　我们的堆中已经有了[5,3,2,1,1],我们现在增加一个元素[6]至堆尾

 

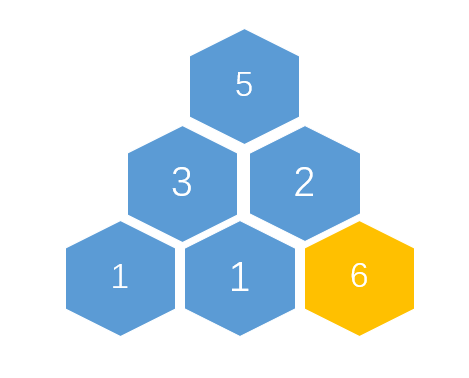
　　此时child=6，所以fa=3，比较更新父子关系：

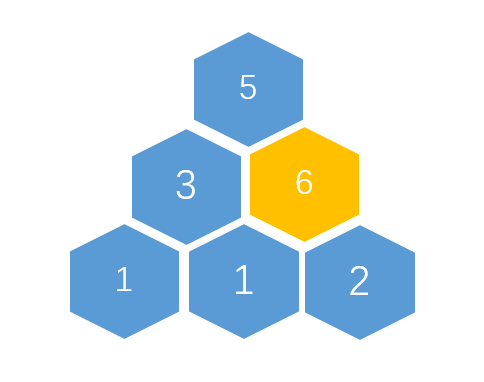
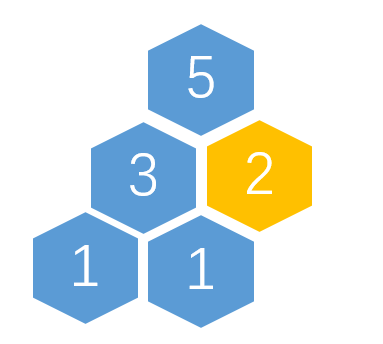
　　此时child=3，,所以fa=1，再次比较更新父子关系：

       

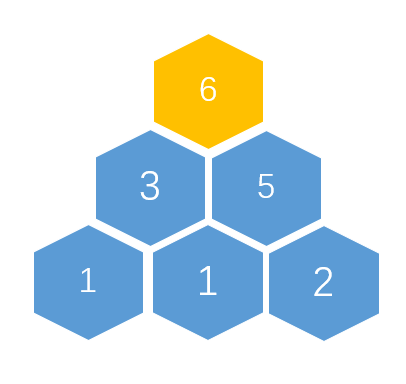
　　此时child已经等于一了，所以我们不在继续更新父子关系。

　　现在，这个结构已经成为了一个完美的大顶堆。

 2.2.获得堆顶值并维护大顶堆

 　　get函数目标效果

1. 取出堆顶值并将其删除；
2. 维护大顶堆关系

　　Code：

int get(){
    int fa,ch;
    int ans = heap[1];
    heap[1] = heap[heap_size--];//便捷方式：用堆尾的值覆盖堆顶值 
    fa = 1;
    while(fa*2<=heap_size){
        ch = fa*2;
        if(ch < heap_size && heap[ch+1] > heap[ch])//选择两个孩子中更大的那一个 
            ch++;
        if(heap[p]>=heap[child])break; //father已经够大了，不需要再继续向下找
        swap(heap[ch],heap[fa]);
        fa = ch;//更新 
    }
    return ans;
}

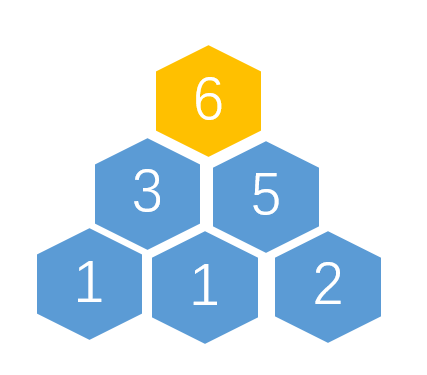
　　如图所示：

 

2.3.小顶堆

　　原理与大顶堆相同，所以——

　　咕。

 3.例题：合并果子

---

 

3.1.题目描述

　　在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

　　每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 n-1 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 1 ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 3 种果子，数目依次为 1 ， 2 ， 9 。可以先将 1 、 2 堆合并，新堆数目为 3 ，耗费体力为 3 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12 ，耗费体力为 12 。所以多多总共耗费体力 =3+12=15 。可以证明 15 为最小的体力耗费值。

　　题目链接

3.2.思路

　　贪心的想法：每次都合并第一小与第二小的数据，然后将合并后的数据加入数据中等待下次合并。

　　所以

　　我们可以考虑小根堆算法。

3.3.代码

　　Code：

#include<cstdio>
#include<iostream>
 
using namespace std;
 
int n,h,a[10001];
 
void put(int c){//小根堆维护 
    int p1,p2;
    h++;
    a[h]=c;//堆内元素个数 
    p1=h;
    while(p1>1){
        p2=p1/2;//p2父亲位置 
        if(a[p1]>=a[p2])return ;//不够小 
        swap(a[p1],a[p2]);
        p1=p2;
    }
}
 
int get(){
    int p=1,next,ans;
    ans=a[1];
    a[1]=a[h];
    h--;
    while(p*2<=h){
        next=p*2;
        if(next<h and a[next+1]<a[next])next++;//选择较小的孩子 
        if(a[p]<=a[next])break;//已经够小 
        swap(a[p],a[next]);
        p=next;
    }
    return ans;
}
 
int main(){
    int c,ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&c);
        put(c);
    }
    while(h>1){
        int one=get();
        int two=get();
        put(one+two);
        ans+=(one+two);
    }
    printf("%d",ans);
    return 0;
}

 

4.口胡：堆排序

---

 

从大到小排序：大顶堆

从小到大排序：小顶堆

#include<cstdio>
#include<iostream>
 
using namespace std;
 
int a[100001],h;
 
void put(int c){
    int p1,p2;
    h++;
    a[h]=c;
    p1=h;
    while(p1>1){
        p2=p1/2;
        if(a[p2]<=a[p1])return;
        swap(a[p1],a[p2]);
        p1=p2;
    }
}
 
int get(){
    int p=1,next,ans;
    ans=a[1];
    a[1]=a[h];
    h--;
    while(p*2<=h){
        next=p*2;
        if(next<h&&a[next+1]<a[next])next++;
        if(a[p]<a[next])break;
        swap(a[p],a[next]);
        p=next;
    }
    return ans;
}
 
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int t;
        cin>>t;
        put(t);
    }
    for(int i=1;i<=n;i++){
        printf("%d ",get());
    }
    return 0;
}

 

　　时间复杂度：O(2×n log n)

---

 

　　-------------The END-----------------