Stirling公式
n!与 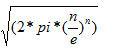
的值十分接近,利用Stirling公式将阶乘转化成幂函数,使得阶乘的结果得以更好的估计。而且n越大,估计得就越准确
用该公式计算n!结果的位数时,可以两边取对数,得:
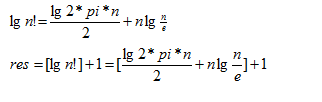
#include<iostream> #include<math.h> using namespace std; const double e=2.7182818284590452354,pi=3.141592653589793239; //e和i的值要精确 double str_ling(int n){ return 0.5*log10(2*pi*n)+n*log10(n/e); } int main(){ int t; while (cin>>t) { cout<<(int)str_ling(t)+1<<endl; } return 0; }




