字符串学习笔记
Post time: 2021-02-02 18:36:35
一切字符串算法的本质都是有效利用失配信息进行匹配或查询!
一、Manacher算法
最长回文子串。暴力是枚举中间点然后左右依次查询,Manacher算法通过之前查询过的中间点来更新后面的。
首先,因为回文串有长度奇偶的区别,所以通过在两两字符之间加 '#' 来化为同种问题。
设之前查到的中间点中匹配的最靠后的为 \(id\),这个最靠后的位置为 \(mx\)。设每个点为中心点的最长回文子串长度为 \(l_i\),则:
若 \(i<mx\),那么我们可以通过 \(i\) 关于 \(id\) 对称的镜像点来给 \(i\) 赋值,即
取 \(\min\) 的原因是只能判断在 \(id\) 已经配完的内部可以,外边不一定可以。
否则,则 \(l_i=1\)。
这样赋完初值之后再向外拓展可以最终得到 \(O(n)\) 复杂度求解最长回文子串。
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define rint register int
using namespace std;
const int N=1.1e7+13;
char s[N<<1],t[N];
int n,l[N<<1];
int manacher(){
rint mx=0,id=0,ans=0;
for(rint i=1;i<=n;++i){
if(i<mx) l[i]=min(l[id*2-i],mx-i);
else l[i]=1;
while(s[i+l[i]]==s[i-l[i]]) ++l[i];
if(i+l[i]>mx) mx=i+l[i],id=i;
ans=max(ans,l[i]);
}
return ans-1;
}
int main(){
scanf("%s",t+1);n=strlen(t+1);
s[0]=s[1]='#';
for(rint i=1;i<=n;++i) s[i*2]=t[i],s[i*2+1]='#';
n=n*2+2;s[n]=0;
printf("%d\n",manacher());
return 0;
}
二、最小表示法
判断两个字符串(可旋转)是否相等。暴力是取出所有可能得到的串,取最小串,看看是否相等。这启发我们可以利用失配信息求最小串:
字符串 \(s\):\(i\) 指针;字符串 \(t\):\(j\) 指针;两个字符串目前已经匹配的长度设为 \(k\)。
若 \(s_{i+k}=t_{j+k}\),则直接 \(++k\)。
若 \(s_{i+k}>t_{j+k}\),那么 \(i...i+k\) 这些都一定不是最小串的开头,直接把 \(i\) 改为 \(i+k+1\)。另一种同理。
模板题中要求一个串的轮换同构串中字典序最小的,直接以此串中两个不同开头的位置做最小表示法,即可最终求得最小串。注意此时两个指针一定不能相等,要特判。
点击查看代码
#include<iostream>
#include<cstdio>
using namespace std;
const int N=3e5+13;
int n,s[N<<1];
inline int minshow(){
int i=1,j=2,k=0;
while(i<=n&&j<=n&&k<n){
if(s[i+k]==s[j+k]) ++k;
else{
if(s[i+k]>s[j+k]) i+=k+1;
else j+=k+1;
if(i==j) ++i;
k=0;
}
}
return min(i,j);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&s[i]);
s[i+n]=s[i];
}
int t=minshow();
for(int i=0;i<n;++i) printf("%d ",s[i+t]);
return 0;
}
三、KMP字符串匹配
匹配两个字符串,暴力就是两个指针 \(i,j\),从头开始匹配,如果不成功再从头开始,这样复杂度 \(O(nm)\)。
如何利用失配信息?首先我们想,当 \(s_i\neq t_j\) 的时候,如果我们固定 \(i\) 单调不减,那么 \(j\) 应该减少的越少越好,因为 \(j\) 减少的越少,相当于此时已经匹配的字符数就越多。这启发我们可以先预处理一部分信息,然后每次失配之后 \(j\) 都跳到这样一个位置上继续匹配。
仔细思考一下这个位置需要满足什么性质。显然,如果设这个位置为 \(k\),那么相当于要找到一个最大的 \(k\) 使其满足 \(t_{1...k}=t_{j-k+1...j}\)。
首先假设我们对于每个 \(i\) 都找到了上述这样一个位置 \(nxt_i\),那么就可以使用一开始说的方法来计算。注意到我们的匹配次数此时是线性的,复杂度O(m)。
考虑如何预处理。可以发现,预处理实际上就是自己匹配自己的过程,两个指针均指向同一字符串,首先定义 \(nxt_1=0\),接下来通过同样的方式做即可,每个位置的 \(nxt\) 值就是当 \(i\) 停留在这个位置时最终的 \(j\) 值。
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e6+13;
char s[N],t[N];
int n,m,nxt[N];
inline void init(){
nxt[1]=0;
for(int i=2,j=0;i<=n;++i){
while(j&&t[j+1]!=t[i]) j=nxt[j];
if(t[j+1]==t[i]) ++j;
nxt[i]=j;
}
}
inline void KMP(){
for(int i=1,j=0;i<=m;++i){
while(j&&t[j+1]!=s[i]) j=nxt[j];
if(t[j+1]==s[i]) ++j;
if(j==n) printf("%d\n",i-n+1),j=nxt[j];
}
}
int main(){
scanf("%s",s+1);m=strlen(s+1);
scanf("%s",t+1);n=strlen(t+1);
init();
KMP();
for(int i=1;i<=n;++i) printf("%d ",nxt[i]);
return 0;
}
四、AC自动机
AC自动机就是在Trie树上对多个子串跑KMP。先建立一个Trie树,然后再Trie树上通过BFS建立fail(相当于KMP中next指针),匹配的具体流程基本等同于KMP。另外,如果一个单词走到了最后一个字母,那么不管是否匹配成功都应该回到它的fail指针。
点击查看代码
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N=1e6+13;
struct Aho_Corasick_Automaton{
#define ACA Aho_Corasick_Automaton
int ch[N][30],fail[N],val[N],cnt;
ACA(){cnt=0;}
inline void ins(char *s){
int len=strlen(s),now=0;
for(int i=0;i<len;++i){
int c=s[i]-'a';
if(!ch[now][c]) ch[now][c]=++cnt;
now=ch[now][c];
}
val[now]++;
}
inline void build(){
queue<int>q;fail[0]=0;
for(int c=0;c<26;++c){
int u=ch[0][c];
if(u) fail[ch[0][c]]=0,q.push(ch[0][c]);
}
while(!q.empty()){
int u=q.front();q.pop();
for(int c=0;c<26;++c){
if(ch[u][c]) fail[ch[u][c]]=ch[fail[u]][c],q.push(ch[u][c]);
else ch[u][c]=ch[fail[u]][c];
}
}
}
inline int query(char *s){
int n=strlen(s),now=0,res=0;
for(int i=0;i<n;++i){
now=ch[now][s[i]-'a'];
for(int j=now;j&&val[j]!=-1;j=fail[j]) res+=val[j],val[j]=-1;
}
return res;
}
}AC;
int n;char s[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%s",s),AC.ins(s);
AC.build();
scanf("%s",s);int ans=AC.query(s);
printf("%d\n",ans);
return 0;
}
五、扩展 KMP
扩展 KMP 可以求出一个子串 \(T\) 对一个子串 \(S\) 的每一个后缀的最长公共前缀。这个算法之所以被称为 \(exKMP\),是因为其与 \(KMP\) 有一些共同特性。
设 \(extend[i]\) 表示 \(T\) 与 \(S[i...n]\) 的最长公共前缀的长度。假设此时我们已经匹配完了 \(extend[1...i-1]\),此时正在匹配 \(i\)。设之前匹配中能够匹配到 \(S\) 串中最远位置的位置为 \(l\),这个最远的位置为 \(r\)。那么此时有:
即
此时求 \(extend[i]\) 即相当于求 \(T[i-l+1...n]\) 与 \(T\) 的最长公共前缀。假设我们已经求出了一个数组 \(nxt\),\(nxt[i]\) 表示 \(T[i...n]\) 与 \(T\) 的最长公共前缀长度,那么在这里相当于是求的 \(nxt[i-l+1]\)。设这个值为 \(tmp\),那么如果 \(i+tmp<=r\) 则证明这个 \(tmp\) 可以取到,否则我们就把 \(ext[i]\) 调到 \(r\) 这个位置,然后继续向后匹配即可。复杂度 \(O(m)\)。
另外,求 \(nxt\) 数组的过程相当于是自己对自己进行一次以上操作,所以复杂度 \(O(n)\)。这就是 \(exKMP\) 和 \(KMP\) 最大的相似之处。
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2e7+13;
char s[N],t[N];
int n,m,nxt[N],ext[N];
inline void init(){
nxt[1]=n;
for(int i=2,l=0,r=0;i<=n;++i){
int tmp=nxt[i-l+1];
if(i<=r){
if(i+tmp<=r) nxt[i]=tmp;
else nxt[i]=r-i+1;
}
while(i+nxt[i]<=n&&t[i+nxt[i]]==t[1+nxt[i]]) ++nxt[i];
if(i+nxt[i]-1>r) r=i+nxt[i]-1,l=i;
}
}
inline void exKMP(){
for(int i=1,l=0,r=0;i<=m;++i){
int tmp=nxt[i-l+1];
if(i<=r){
if(i+tmp<=r) ext[i]=tmp;
else ext[i]=r-i+1;
}
while(i+ext[i]<=m&&1+ext[i]<=n&&s[i+ext[i]]==t[1+ext[i]]) ++ext[i];
if(i+ext[i]-1>r) r=i+ext[i]-1,l=i;
}
}
inline void file(){
freopen("P5410_1.in","r",stdin);
freopen("P5410.out","w",stdout);
}
int main(){
//file();
scanf("%s%s",s+1,t+1);
m=strlen(s+1),n=strlen(t+1);
init();
exKMP();
long long ans1=0,ans2=0;
for(int i=1;i<=n;++i) ans1^=1ll*i*(nxt[i]+1);
for(int i=1;i<=m;++i) ans2^=1ll*i*(ext[i]+1);
printf("%lld\n%lld\n",ans1,ans2);
return 0;
}
六、子序列自动机
\(q\) 次询问一个数组 \(S\) 是不是 \(T\) 的子序列。
考虑先对 \(T\) 中出现的值维护一个下标集合,每次进来 \(S\) 之后从前往后扫,在当前位二分搜索当前值在 \(T\) 中的下标集合中第一个大于当前位置的位置,把指针移过去。一直这样做看看能否移到最后即可。
点击查看代码
#include<cstdio>
#include<iostream>
#include<vector>
#include<algorithm>
inline int rd(){
int res=0;char c=getchar();
for(;!isdigit(c);c=getchar());
for(;isdigit(c);c=getchar())res=(res<<1)+(res<<3)+(c-'0');
return res;
}
const int N=1e5+13,M=1e6+13;
int n,q,m,b[N];
std::vector<int> pos[N];
int main(){
int useless=rd();n=rd(),q=rd(),m=rd();
for(int i=1;i<=n;++i) pos[rd()].push_back(i);
while(q--){
int len=rd();
for(int i=1;i<=len;++i) b[i]=rd();
if(len>n){puts("No");continue;}
bool flag=1;
for(int i=1,j=0;i<=len;++i){
if(pos[b[i]].empty()){flag=0;break;}
std::vector<int>::iterator now=std::upper_bound(pos[b[i]].begin(),pos[b[i]].end(),j);
if(now==pos[b[i]].end()){flag=0;break;}
j=*now;
}
puts(flag?"Yes":"No");
}
return 0;
}
七、后缀自动机
后缀自动机(SAM)是一个有限状态自动机,表示为一个有向图,分两部分:DAWG 和 parent 树。后缀自动机的定义是接受且仅接受串 \(S\) 的所有子串,最小化节点个数。
DAWG 是一个 DAG。每个节点表示一个或多个 \(S\) 的子串。起始节点对应 \(\varnothing\)。每条转移边都只代表一个字符。从起始节点开始的每一条路径都唯一对应 \(S\) 的某个子串(或者说,某些本质相同的子串)。每个节点代表的字符串是某些前缀长度连续的后缀,每个点维护三个信息:\(\min_u,\max_u\) 分别表示最小和最大长度的串,\(\mathrm{end}_ u\) 表示这个节点表示的前缀集合。
定理 1 任意两个点的 \(\mathrm{end}\) 集合互不相同。
证明:相同的话直接合并即可。
parent 树是一棵树。\(u\) 的 parent 指针指向 \(v\) 当且仅当 \(|\min_u|=|\max_v|+1\),且 \(v\) 代表的子串均为 \(u\) 代表的子串的后缀,记作 \(\mathrm{next}_ u=v\)。所有节点作为以起始节点的为根的树,所以称为 parent 树。
定理 2 \(\mathrm{end}_ u\subsetneqq \mathrm{end}_ {\mathrm{next_ u}}\)
这个很显然吧。真包含而不是包含是因为定理 1。
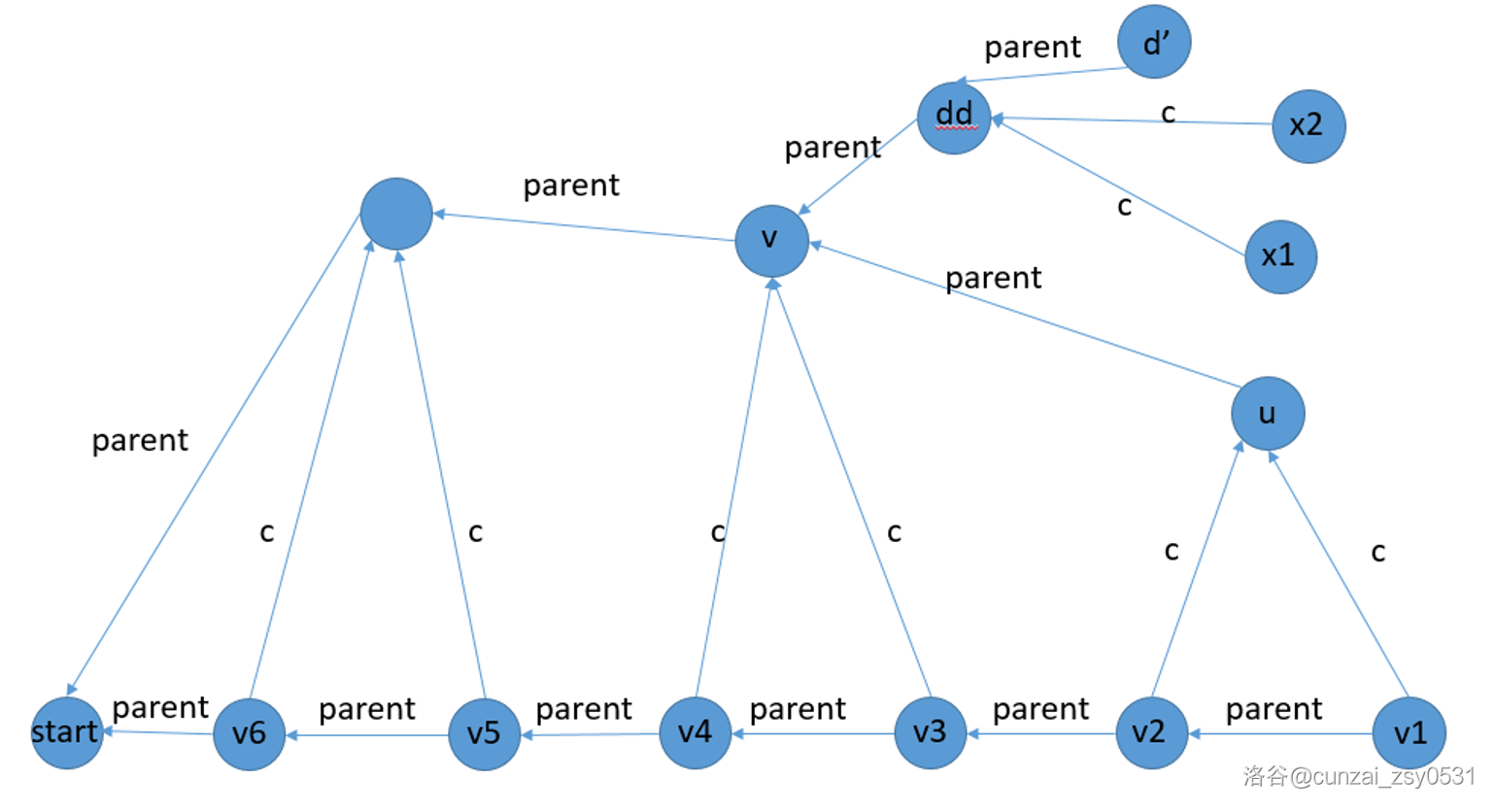
SAM 的构建:增量法。考虑在已经建出的 \(S\) 的 SAM 上扩展出 \(S+c\) 的 SAM。考虑下图:
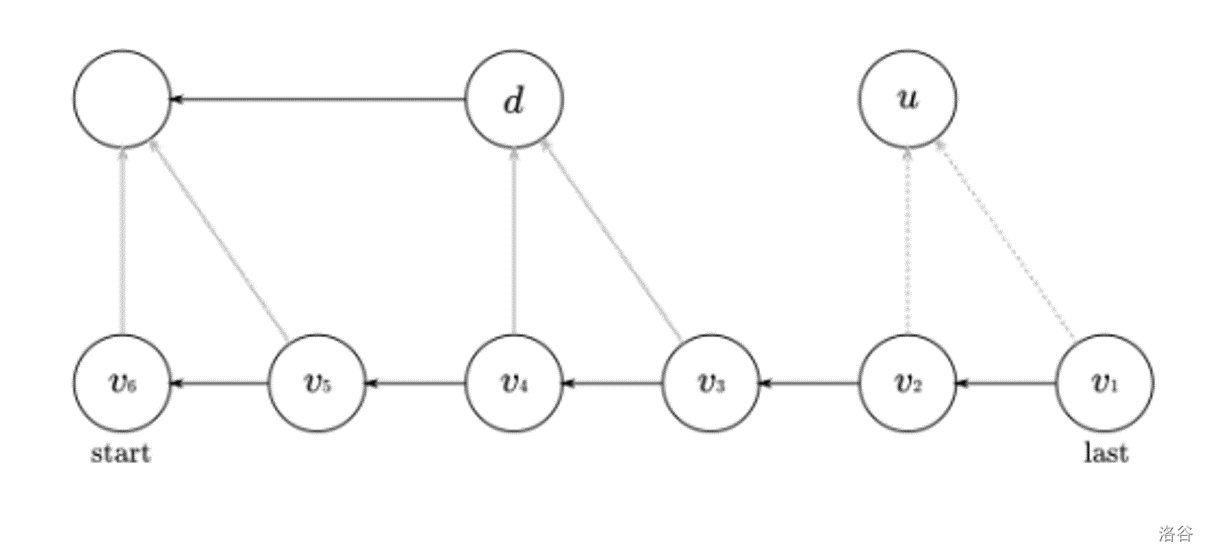
\(start\) 节点就是 SAM 的初始节点。\(v_1,v_2,\ldots,v_m\) 指的是 \(S\) 所有后缀在的点,首先一定存在一个 \(v_1\) 没有 \(c\) 的转移边,我们设 \(v_1\sim v_2\) 这一段的点都没有 \(c\) 的转移边,\(v_3\sim v_6\) 是有转移边。接下来考虑三种情况:
Case 1:没有 \(v_3\)
即 \(start=v_2\),扩展出来的 \(u\) 点的 parent 应该为 \(start\)。
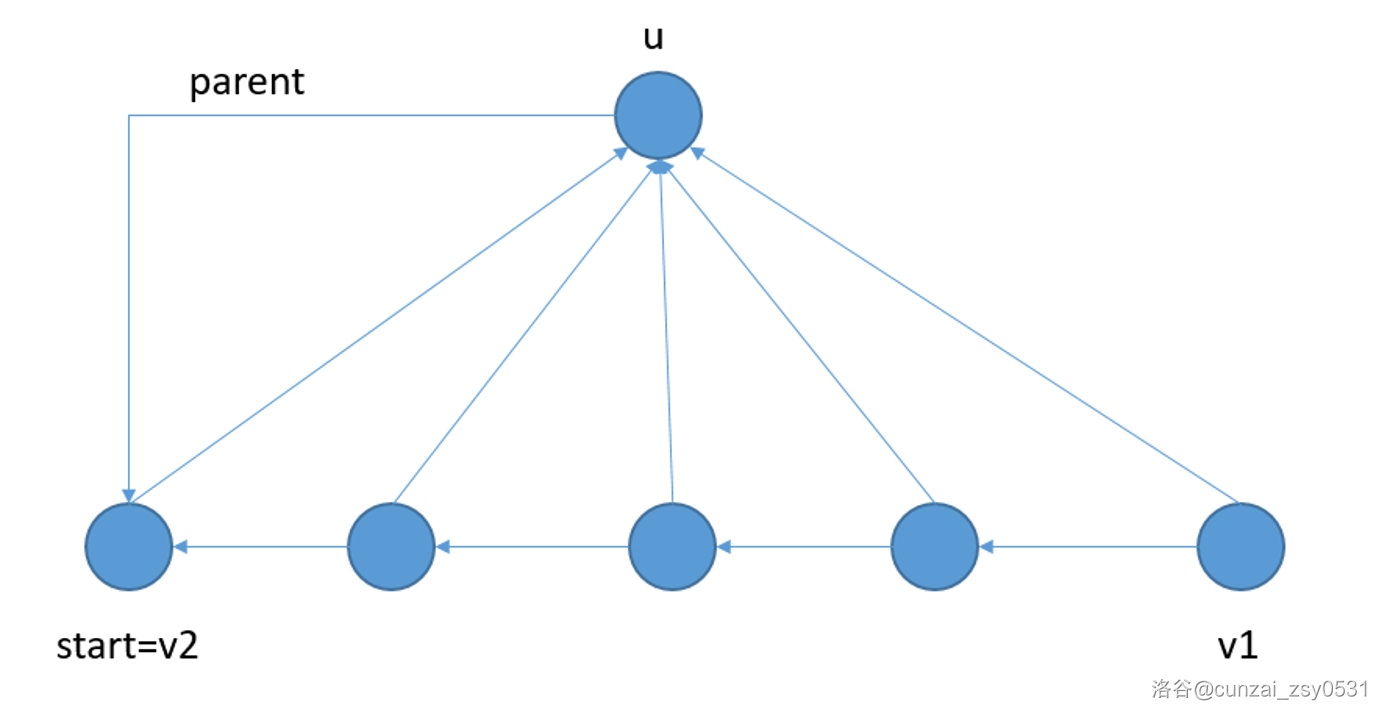
Case 2:\(\max_{d}=\max_{v3}+1\)
这个就正常建,然后把 \(u\) 的 parent 设成 \(d\)。
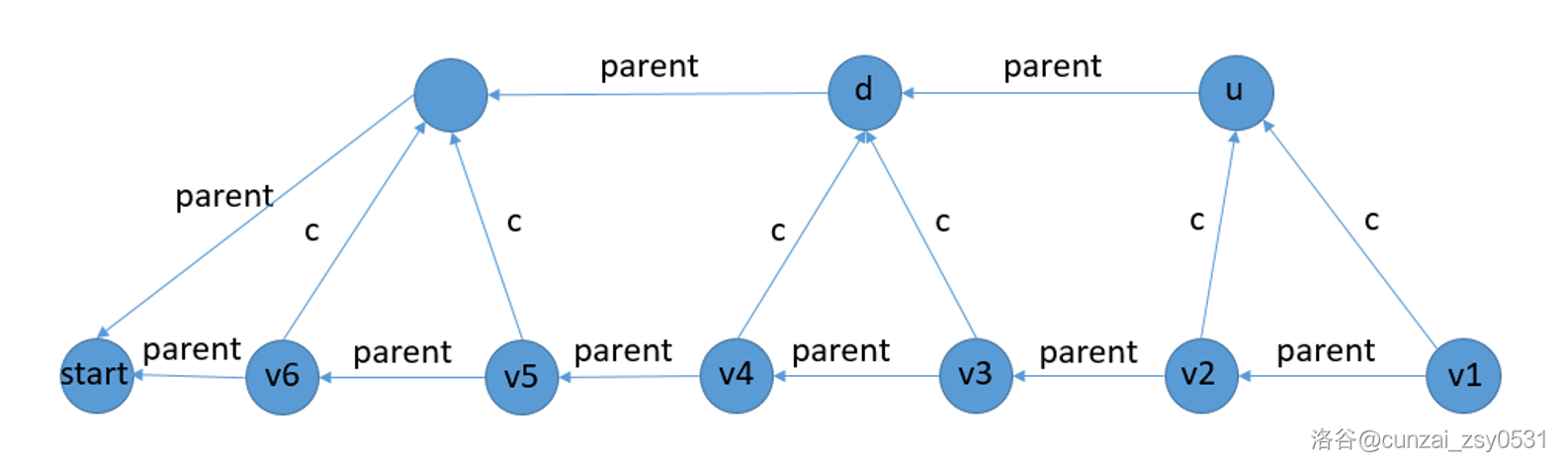
Case 3: \(\max_d\not= \max_{v3}+1\)
也就是说,本来是这样:
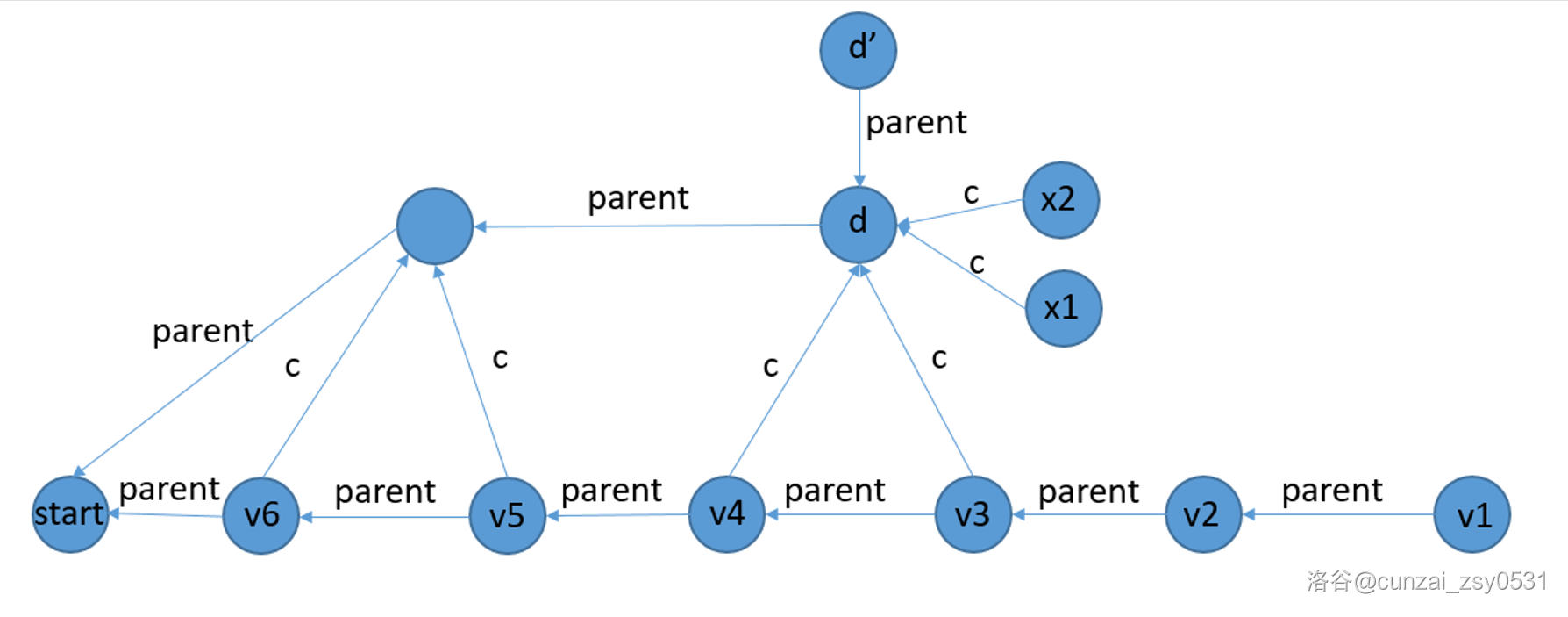
然后,\(v3+c\) 和 \(x1+c,x2+c\) 的 \(\mathrm{end}\) 集合出现了变动,这时候我们需要把 \(d\) 裂成两个点 \(v,dd\),其中 \(v3\to v\) 表示 \(\mathrm{end}\) 集合发生变动的那些后缀,\(dd\) 是剩下的那些,然后就变成了这样:
my SAM code:
点击查看代码
inline int newpos(std::array<int,M> nson,int nlen){return ++ptot,len[ptot]=nlen,swap(son[ptot],nson),ptot;}
inline void insert(int c){
int p=lastpos;int u=newpos(boom,len[p]+1);cnt[u]=1;
while(p&&!son[p][c]) son[p][c]=u,p=nxt[p];
if(!p) return lastpos=u,nxt[u]=1,void();
int d=son[p][c];
if(len[d]==len[p]+1) nxt[u]=d;
else{
int v=newpos(son[d],len[p]+1);
nxt[v]=nxt[d],nxt[d]=v,nxt[u]=v;
while(p&&son[p][c]==d) son[p][c]=v,p=nxt[p];
}
lastpos=u;
}
八、后缀数组
终于还是因为有道题需要使用SA+st表而不能使用SAM来补了SA……
定义:
\(sa[i]\) 表示所有后缀排序后从小到大第 \(i\) 个后缀的编号,\(rk[i]\) 表示第 \(i\) 个后缀的排名。
首先把所有后缀的第一位拿出来排一下序,更新 \(sa[i]\) 和 \(rk[i]\)。注意这里的 \(rk[i]\),如果当前是相等的那么就令两个位置 \(rk\) 相等。
接下来考虑一个倍增:第 \(i\) 次排序考虑所有后缀长度为 \(2^i\) 的前缀,由于上一次排序排了长度为 \(2^{i-1}\) 的,所以每个位置相当于是一个 pair,表示前 \(2^{i-1}\) 和后 \(2^{i-1}\) 的排名。然后这个双关键字排序可以使用桶排序 \(O(n)\) 解决,所以总复杂度 \(O(n\log n)\)。
细节:双关键字桶排序的过程,首先按照第二关键字从小到大排序(如果长度不足 \(2^n\),第二关键字就是 \(0\)),然后直接做桶排即可。
code:
点击查看代码
char s[N];
int n,sa[N],rk[N],_rk[N<<1],id[N],tmp[N],tong[N];
inline bool cmp(const int &x,const int &y,const int &z){return _rk[x]==_rk[y]&&_rk[x+z]==_rk[y+z];}
inline void SA(){
int m=200;
for(int i=1;i<=n;++i) ++tong[rk[i]=s[i]];
for(int i=2;i<=m;++i) tong[i]+=tong[i-1];
for(int i=n;i;--i) sa[tong[rk[i]]--]=i;
for(int w=1,p=0;;w<<=1,m=p,p=0){
for(int i=n;i>n-w;--i) id[++p]=i;
for(int i=1;i<=n;++i) if(sa[i]>w) id[++p]=sa[i]-w;
for(int i=1;i<=m;++i) tong[i]=0;
for(int i=1;i<=n;++i) ++tong[tmp[i]=rk[id[i]]];
for(int i=2;i<=m;++i) tong[i]+=tong[i-1];
for(int i=n;i;--i) sa[tong[tmp[i]]--]=id[i];
memcpy(_rk,rk,sizeof rk);rk[sa[1]]=(p=1);
for(int i=2;i<=n;++i) rk[sa[i]]=(cmp(sa[i],sa[i-1],w)?p:++p);
if(p==n){for(int i=1;i<=n;++i) sa[rk[i]]=i;break;}
}
}
接下来就是重头戏:利用后缀数组求两个后缀的 lcp。
定义一个数组 \(height[i]=lcp(sa[i],sa[i-1])\),即排名 \(i-1\) 和 \(i\) 的 lcp。
定理 1
意义就是后缀 \(i\) 和它在后缀排序之后的前缀的 lcp 长度大于等于后缀 \(i-1\) 和它前缀的 lcp 长度 \(-1\)。
设后缀 \(i-1\) 为 \(aAD\),其中 \(a\) 表示任意一个字符,\(A\) 表示一个长度为 \(height[rk[i-1]]-1\) 的串,\(D\) 是任意串。可以得知后缀 \(i\) 为 \(AD\),后缀 \(sa[rk[i-1]-1]\)(后缀 \(i-1\) 排序后的前缀)为 \(aAB\)(这样公共部分就是 \(aA\),长度 \(height[rk[i-1]]\),并且字典序 \(B<D\))。由于后缀 \(sa[rk[i-1]-1]+1\)(后缀 \(i-1\) 前缀去掉一个第一个字符的后缀)是 \(AB\),包含一个 \(A\) 并且 \(B<D\),所以它应该是在后缀 \(i\) 之前,那么后缀 \(i\) 与它的前缀的 lcp 至少有一个 \(A\),也就证明了上述定理。
定理 2
证明的话就可以先证一下 \(lcp(sa[i],sa[j])=\min_{k=i+1}^j\{lcp(sa[k-1],sa[k])\}\),这个就感性理解一下……
这样的话就可以 \(O(n\log n)\) 预处理,\(O(1)\) 查询任意两个后缀的 lcp 了。

